直升机中减飞溅润滑流场分析与优化方法
2020-12-01陆凤霞王孟王春雷李玉哲朱如鹏
陆凤霞,王孟,王春雷,李玉哲,朱如鹏
1. 南京航空航天大学 直升机传动技术重点实验室,南京 210016 2. 中国航发湖南动力机械研究所,株洲 412002
直升机中间减速器由于功重比高、空间紧凑且结构复杂的特点,通常采用飞溅润滑方式。现有静态润滑设计中,存在锥齿轮高速转动引起的中减内部油气两相流动机理不明、轴承润滑冷却不足、传动效率降低等问题,导致无法准确预测中减内部的滑油分布、润滑效果及回油能力,严重时甚至因润滑不足导致轴承失效,对直升机传动系统的高可靠性需求造成极大威胁。
目前,国内外学者已经采用计算流体力学(Computational Fluid Dynamics, CFD)方法对齿轮箱的流场特性进行了分析并取得了一定的成果。孙凯等[1]应用动网格技术对非正交螺旋锥齿轮中减速器飞溅润滑内部流场进行了动态数值仿真分析,得到了转速对流场分布的影响;董春锋等[2]对齿轮箱油浴润滑的内部流场进行了CFD仿真模拟,研究了齿轮箱内瞬时油液分布以及油压、流速变化规律;姜义尧等[3]基于CFD方法,运用多相流模型和湍流模型建立了中减速器飞溅润滑数值仿真模型,得到了中减速器飞溅润滑过程中的流场特性;彭钱磊等[4]采用齿面移动法分析了齿轮箱飞溅润滑流场特性,通过仿真得到的齿轮阻力矩与试验对比,说明采用分离法和齿面移动法获得的润滑油飞溅效果更加符合实际情况;罗攀等[5]以飞溅润滑复杂齿轮箱为研究对象,采用CFD方法对其内部飞溅润滑流场进行了仿真分析,并通过高速摄影机拍摄箱体内润滑油的运动轨迹验证了仿真的准确性;鲍和云等[6]基于CFD方法对浸油润滑齿轮箱的内部流场进行了动态数值模拟,结果表明运用动网格技术可以较好地对齿轮箱中的油液分布、速度场和压力场进行仿真分析;刘中令等[7]建立了齿轮箱的二维多相流(Volume of Fluid, VOF)模型,采用CFD方法对齿轮箱内部流场进行了仿真分析,计算了齿轮箱在启动低速、常规中速、最高转速工况下的流场动态特性;Li等[8]通过CFD方法对齿轮箱的两相流动进行了研究,通过高速摄像机等设备进行了可视化试验,结果表明仿真与试验具有很好的一致性;Liu等[9]基于粒子法建立了计算流体力学模型,研究了变速箱内润滑油的分布与搅油损失,得到了不同转速与油温下的计算结果,并进行了试验验证,仿真与试验显示出很好的一致性;Peng等[10]提出了一种基于CFD方法模拟准双曲面齿轮箱内飞溅润滑的数值方法,得到了润滑油的分布,并计算了搅油损失,设计了试验台观察齿轮箱内油的分布情况,并测量了齿轮的搅油损失,表明该方法能够准确预测准双曲面齿轮箱的复杂润滑情况,为计算搅油损失提供了一种数值方法;Yang和Hu[11]采用CFD方法结合动网格模型和离散相模型(Discrete Phase Model,DPM),在齿轮箱润滑流场中加入不同粒径的颗粒,仿真计算出颗粒的运动轨迹和分布,表明齿轮箱内颗粒的运动非常复杂,颗粒均呈离心运动趋势,粒子的平均运动速度与齿轮转速和中心距呈非线性正、负关系;Hu等[12]基于CFD方法预测了螺旋锥齿轮的搅油功率损失,获得了中减内部的润滑油分布,并分析了齿轮输入转速、供油量、油液密度黏度及直升机倾斜角度等因素对搅油功率损失的影响规律。
CFD方法已能成功预测齿轮箱内部的压力分布及速度分布,但仅对流场作简单的参数定性影响分析,难以建立以优化润滑冷却性能为目标的参数设计方法,鲜见面向含螺旋锥齿轮、双列圆锥滚子轴承及机匣内壁复杂对象的CFD仿真分析及优化设计方法。为保证中减具备良好的润滑冷却性能,本文建立反映机匣结构的中减CFD复杂计算模型,研究在不同浸油深度及输入转速工况下中减内部的两相流流场分布特性;在中减试验台上开展流场试验,验证CFD方法的可行性;并形成优化中减飞溅润滑性能的参数定量设计范围,为中减两相流动及参数设计提供一种通用的计算方法及优化思路。
1 中减CFD分析模型
1.1 计算模型
直升机中间减速器如图1所示,主要包括机匣、端盖、螺旋锥齿轮和双列圆锥滚子轴承等零件。螺旋锥齿轮将润滑油搅动,飞溅至齿面啮合处进行润滑冷却,但轴承距离齿轮较远,润滑油无法准确飞溅至滚动体-滚道润滑,故通过在端盖上设置导油管将润滑油引流至轴承接触界面,以此对轴承进行润滑与冷却。

图1 中减结构示意图Fig.1 Diagram of intermediate gearbox structure
以某型直升机中减为研究对象,为得到中减机匣内部油气两相流分布、导油管的流量以及齿面的润滑油体积分数,选取机匣、螺旋锥齿轮和导油管为主要研究对象,通过布尔运算得到中减CFD计算模型,如图2所示。由于1号导油管和2号导油管共同润滑主动轮侧的轴承,将其合称为导油管I;3号导油管和4号导油管共同润滑从动轮侧的轴承,将其合称为导油管II。其中螺旋锥齿轮的参数如表1所示。1号、2号导油管直径为6 mm,3号、4号导油管直径为7 mm。由于中减机匣的形状不规则,因此只给出其主要尺寸:机匣最大长度为260 mm,最大高度为282 mm,最大宽度为235 mm。
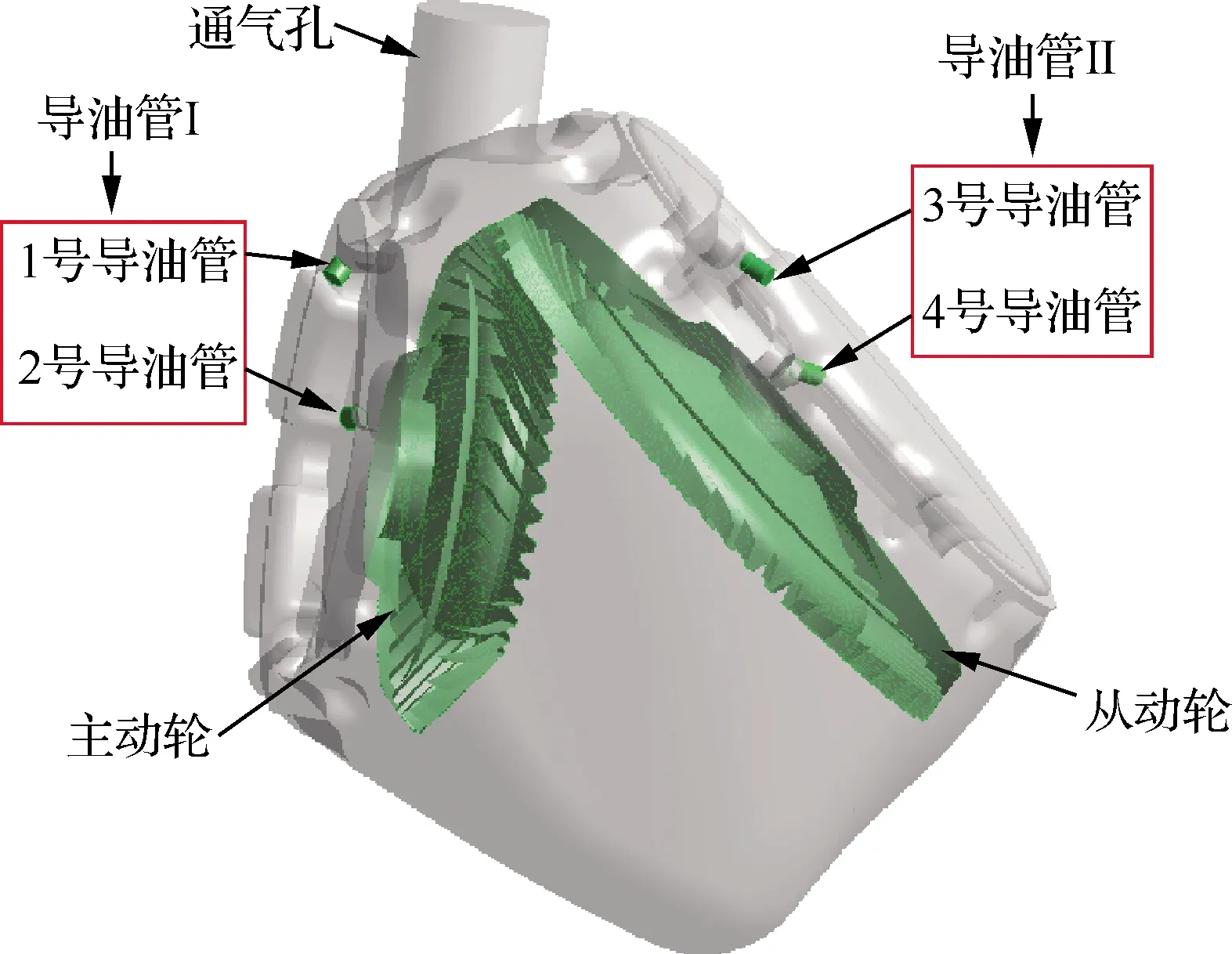
图2 中减CFD计算模型Fig.2 CFD computational model of intermediate gearbox
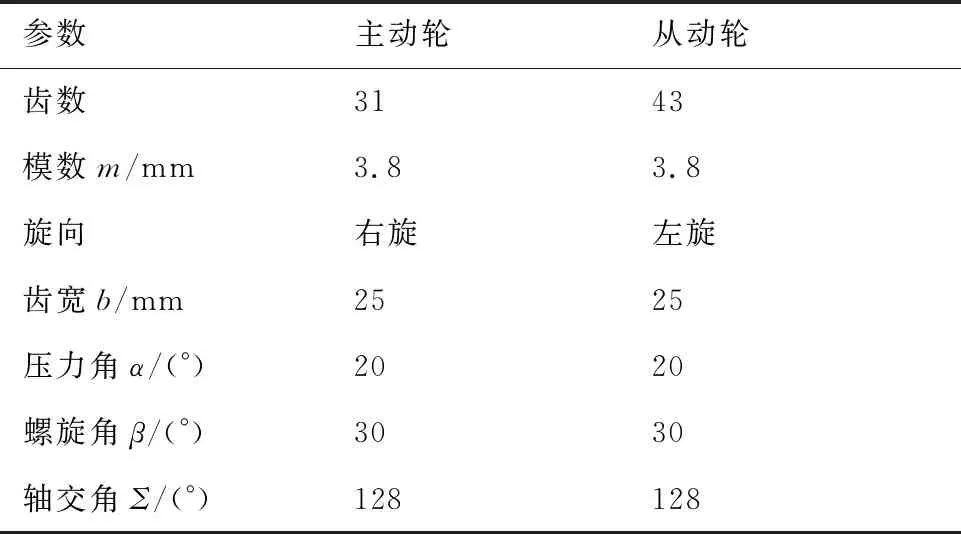
表1 螺旋锥齿轮参数Table 1 Parameters of spiral bevel gears
1.2 网格划分
采用ANSYS Meshing软件对模型进行网格划分。由于中减结构复杂,故采用非结构化四面体网格以适应其复杂结构形状,网格横截面如图3所示。螺旋锥齿轮啮合区间隙较小给网格划分与计算带来极大的困难,因此需对齿轮啮合间隙进行处理。目前常见的处理方法有无齿法[13]、单向切齿法[14]、双向切齿法[15]以及分离法[2,16]。前3种方法对齿轮模型的改变较大,无法体现齿轮的真实结构;因此为提高网格的划分精度,在不影响计算精度的前提下,采用分离法对螺旋锥齿轮啮合区进行处理。
计算过程中齿轮边界的网格扭曲度极大,为防止负体积现象的出现,对齿轮附近的网格进行局部加密,以保证齿轮间隙至少存在2~3层网格;同时,导油管处存在较大的湍动能,且又是流场计算的关键部位,因此对导油管处亦进行局部加密,如图4所示。

图3 网格横截面Fig.3 Symmetrical cross-section mesh

图4 导油管处局部细化的网格Fig.4 Mesh refined locally for oil guide tube
为排除网格密度对计算结果的影响,以通气孔的流量为监测物理量,进行网格无关性验证,结果如图5所示。可以看出,当网格数量为110万左右时,继续增加网格数量,通气孔的流量基本不发生变化。然而网格数量越多,计算时间越长,因此最终的网格数量为1 142 223。
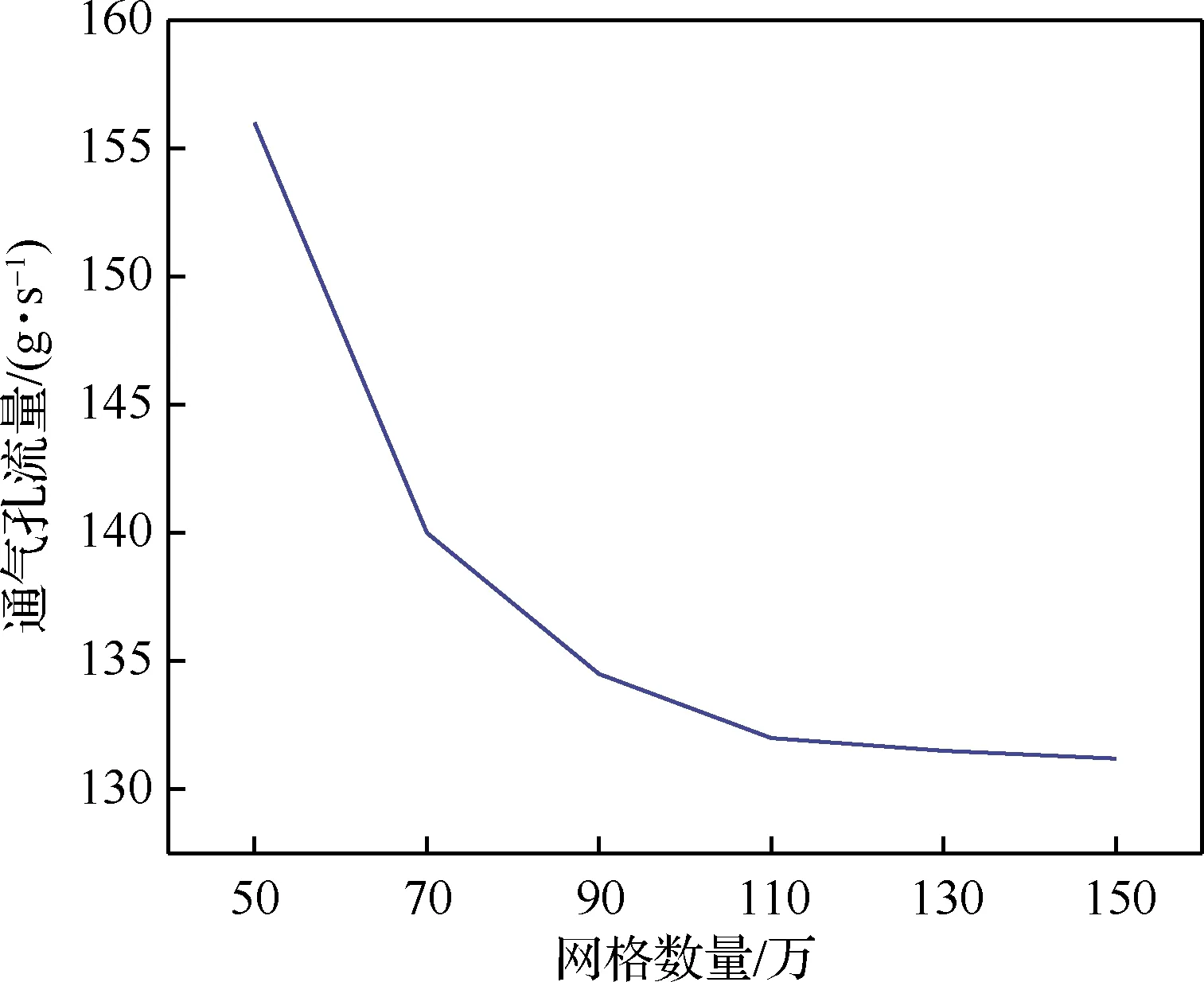
图5 网格无关性验证结果Fig.5 Grid independence verification result
1.3 仿真设置
采用Fluent软件进行数值计算。仿真油温为60 ℃,该温度下润滑油的密度为875.15 kg/m3,动力黏度为0.025 1 kg/(m·s)。初始浸油深度为17 mm(从主动轮最下端计算),初始油液面分布如图6所示。
边界条件的设定会影响求解结果的精确度,为尽可能还原中减运行过程的实际工作状况,进行如下边界条件设置:① 通过编写用户自定义文件(User Defined Functions, UDF)定义螺旋锥齿轮运动边界;② 将通气孔设置为Pressure-outlet,平衡内外大气压;③ 导油管是出油端,将其设置为Pressure-outlet。具体设置方案如图7所示。
考虑到螺旋锥齿轮高速旋转和旋流的影响,选择重整化群(Renormalization-Group,RNG)k-ε湍流模型,该模型可以更好地处理高应变率和流线弯曲程度较大的流动问题。采用Second Order Upwind格式对控制方程离散,采用Geo-Reconstruct格式对VOF方法离散。设定时间步长为3×10-6s,在计算过程监测残差曲线,收敛精度为10-3。在CPU为48核、内存为128 G的计算机上计算主动轮旋转20圈所需时间约168 h。
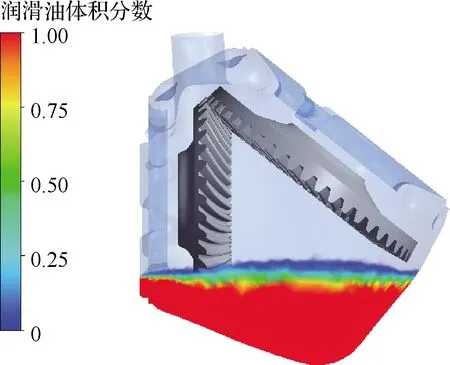
图6 初始油液面分布Fig.6 Initial oil liquid level distribution
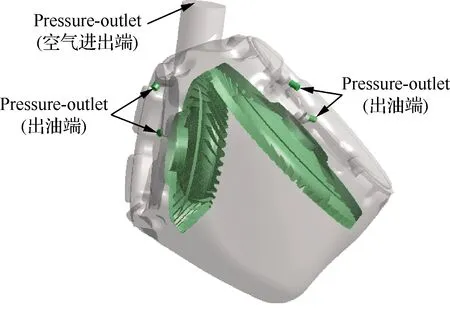
图7 边界条件Fig.7 Boundary conditions
2 CFD理论
2.1 控制方程
虽然直升机中减内部流体流动形态复杂,但仍应满足Navier-Stokes控制方程,包含质量守恒方程、动量守恒方程和能量守恒方程[17]:
(1)
(2)
(3)
式中:ρ为密度,kg/m3;t为时间,s;u为速度矢量,m/s,u=[u1,u2,u3];μ为流体动力黏度,Pa·s;p为流体微元体上的压力,Pa;xi为各方向上的坐标,其中i=1,2,3,分别代表x、y和z方向;Si为广义源项,kg/(m2·s2);T为温度,K;k为流体的传热系数,W/(m2·K);c为比热容,J/(kg·K);ST为黏性耗散项,W。
由于仅研究机匣内的流体流动,工作温度可预先定义,故不考虑能量方程[18]。
2.2 动网格模型
为真实反映螺旋锥齿轮边界的连续转动,采用动网格模型。
当齿轮转动角度较小时,采用弹簧光顺模型处理边界附近变形网格,基本原理为将节点之间的连接视为理想弹簧,通过计算平衡方程对节点位置进行更新[19]。弹簧力与节点位置更新的计算方法为
(4)
(5)
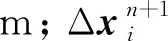
当齿轮转动角度较大时,采用局部网格重构模型,基本原理为将齿轮边界附近的网格根据其网格高度h分裂出新的网格或与相邻的网格合并,即当h≥(1+αh)Hideal(其中:h为当前网格高度;αh为高度系数;Hideal为理想的网格高度)时,网格将进行分裂;当h<(1+αh)Hideal时,网格将与相邻的网格合并。
2.3 VOF多相流模型
为模拟中减飞溅润滑复杂的油-气混合介质流动问题,采用Hirt和Nichols[20]提出的VOF模型。该模型是一种在固定欧拉网格下的表面跟踪方法,通过求解单独的动量方程和处理穿过区域的每一流体的容积比模拟无法混合的流体,将单位体积内的润滑油分子转化为大润滑油分子,并设定该大润滑油分子的速度为参考速度[21],其基本原理如图8所示。
由于计算模型中仅含有油-气两相流,因此VOF模型求解时的控制方程为
(6)
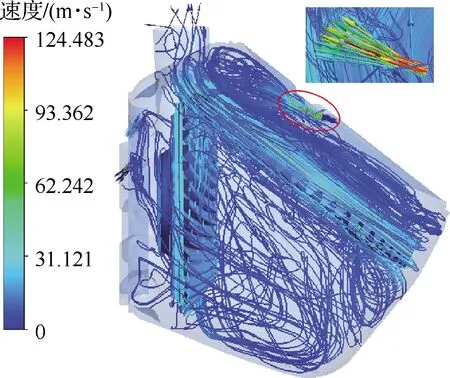
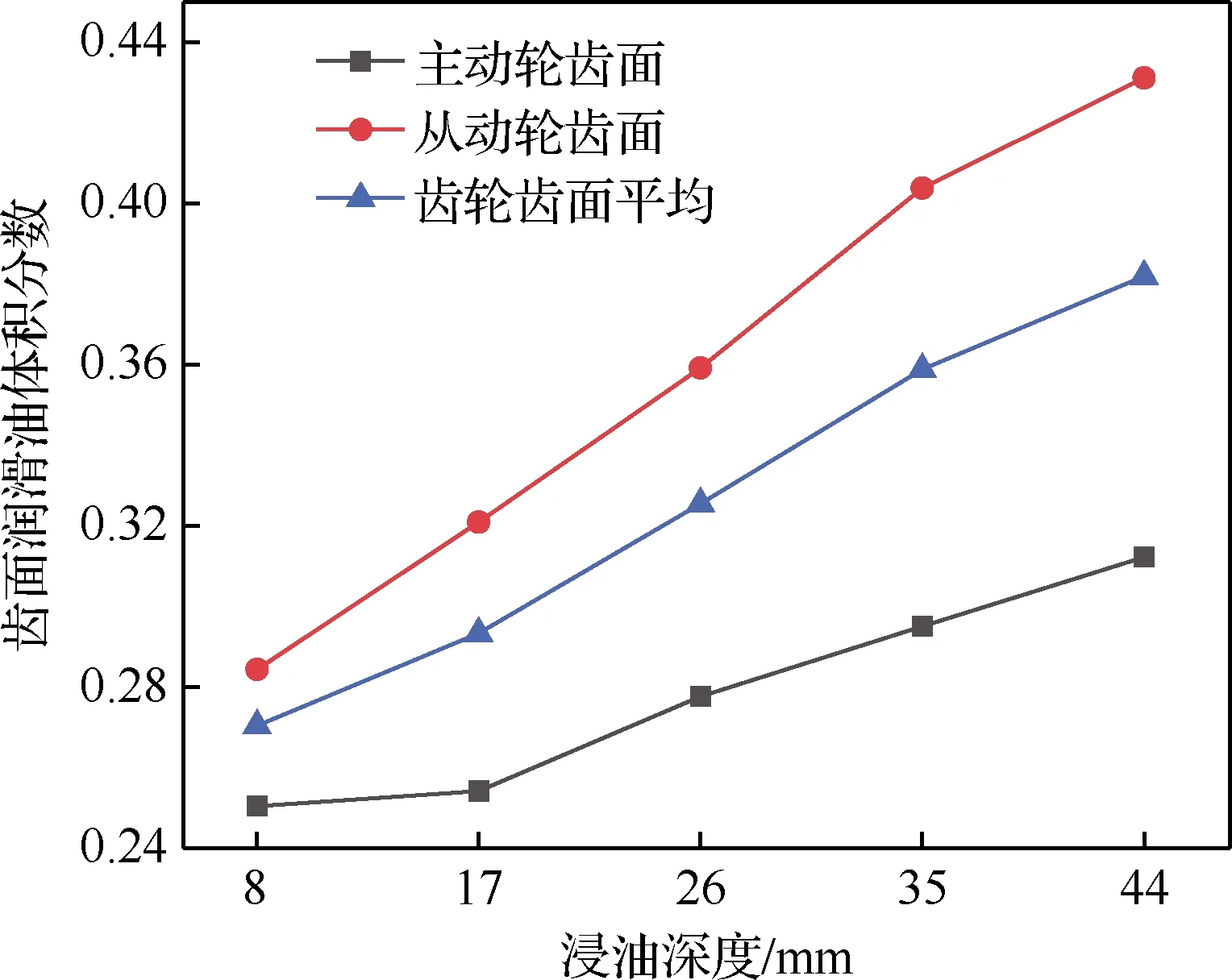
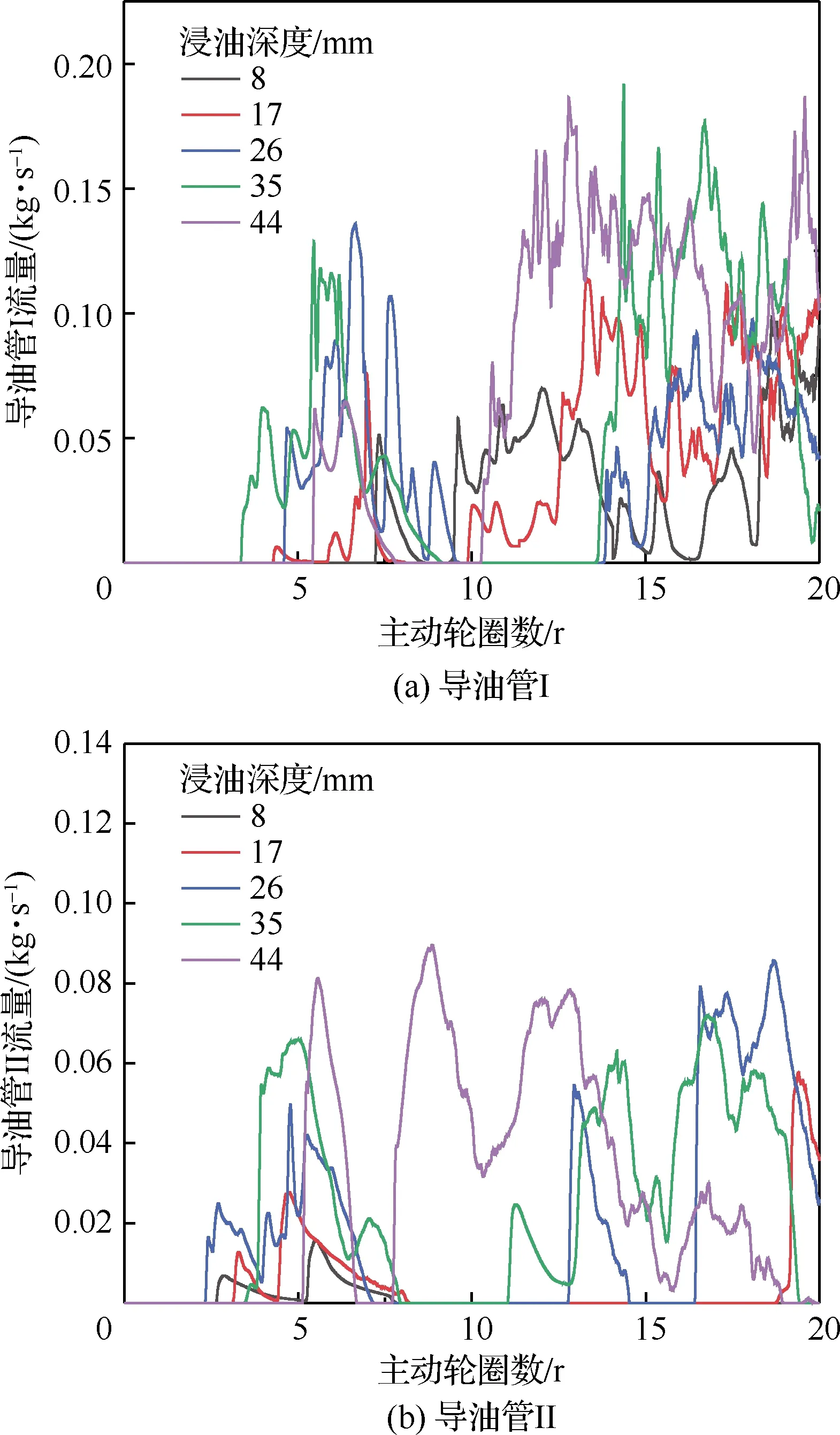
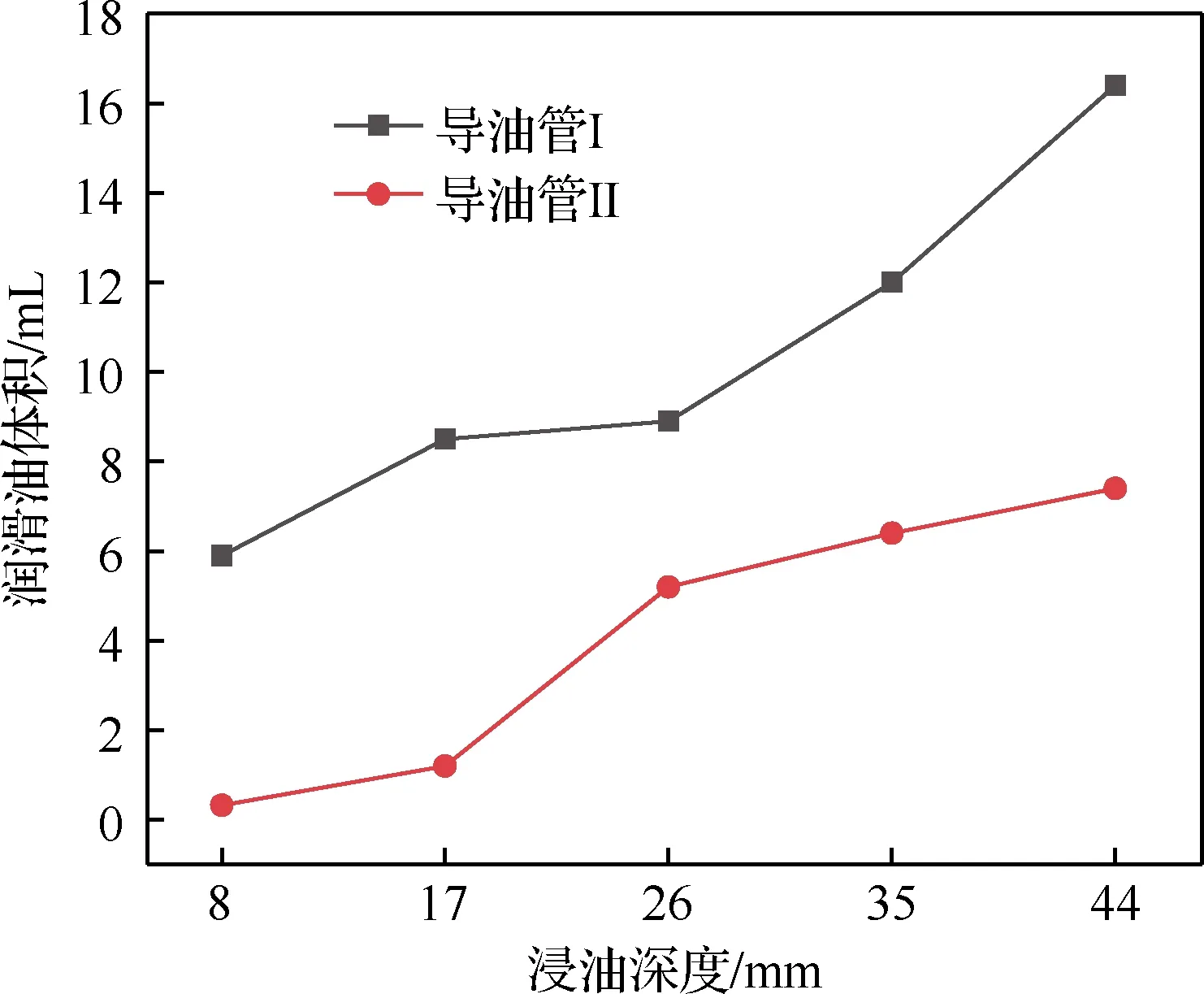
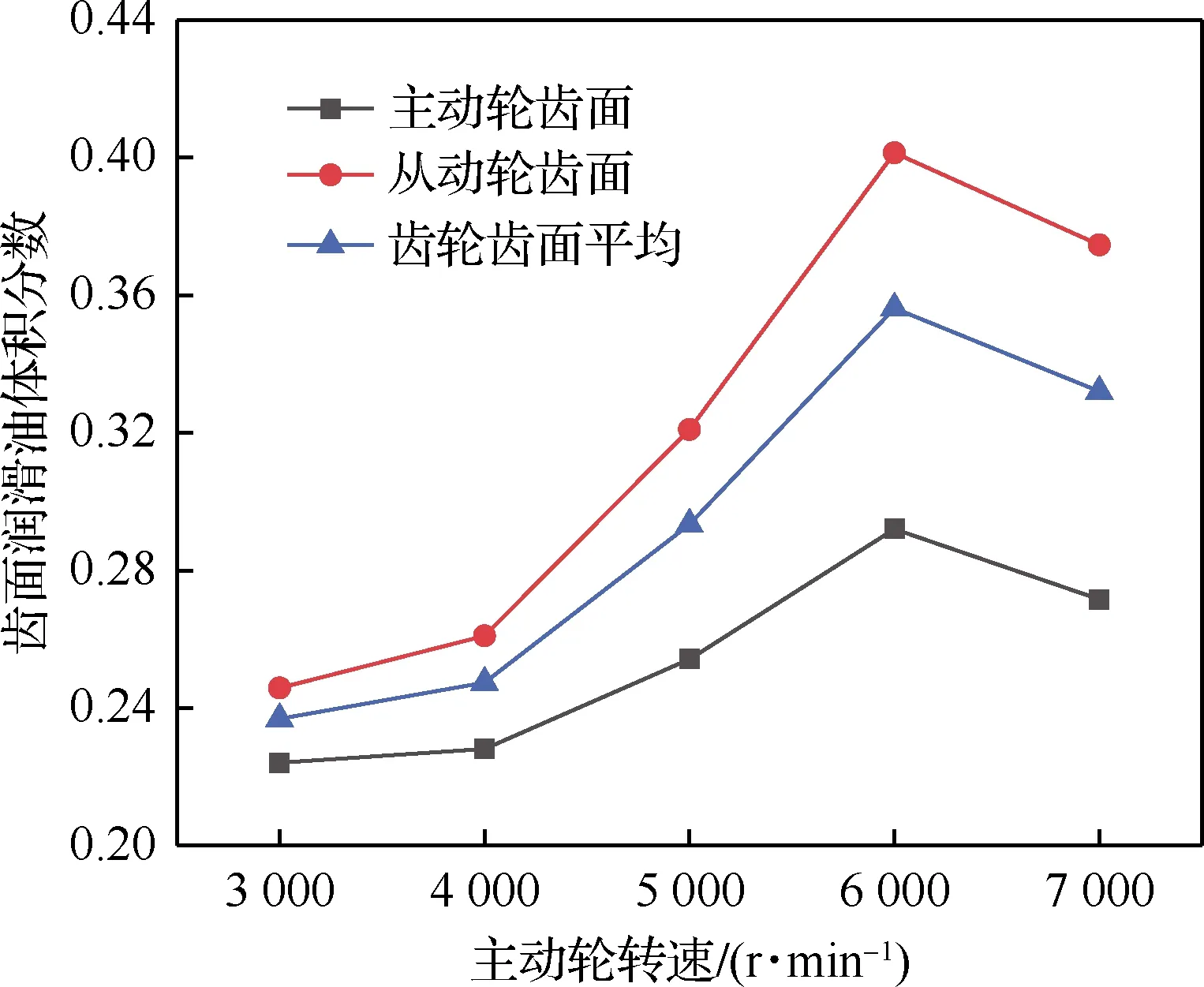
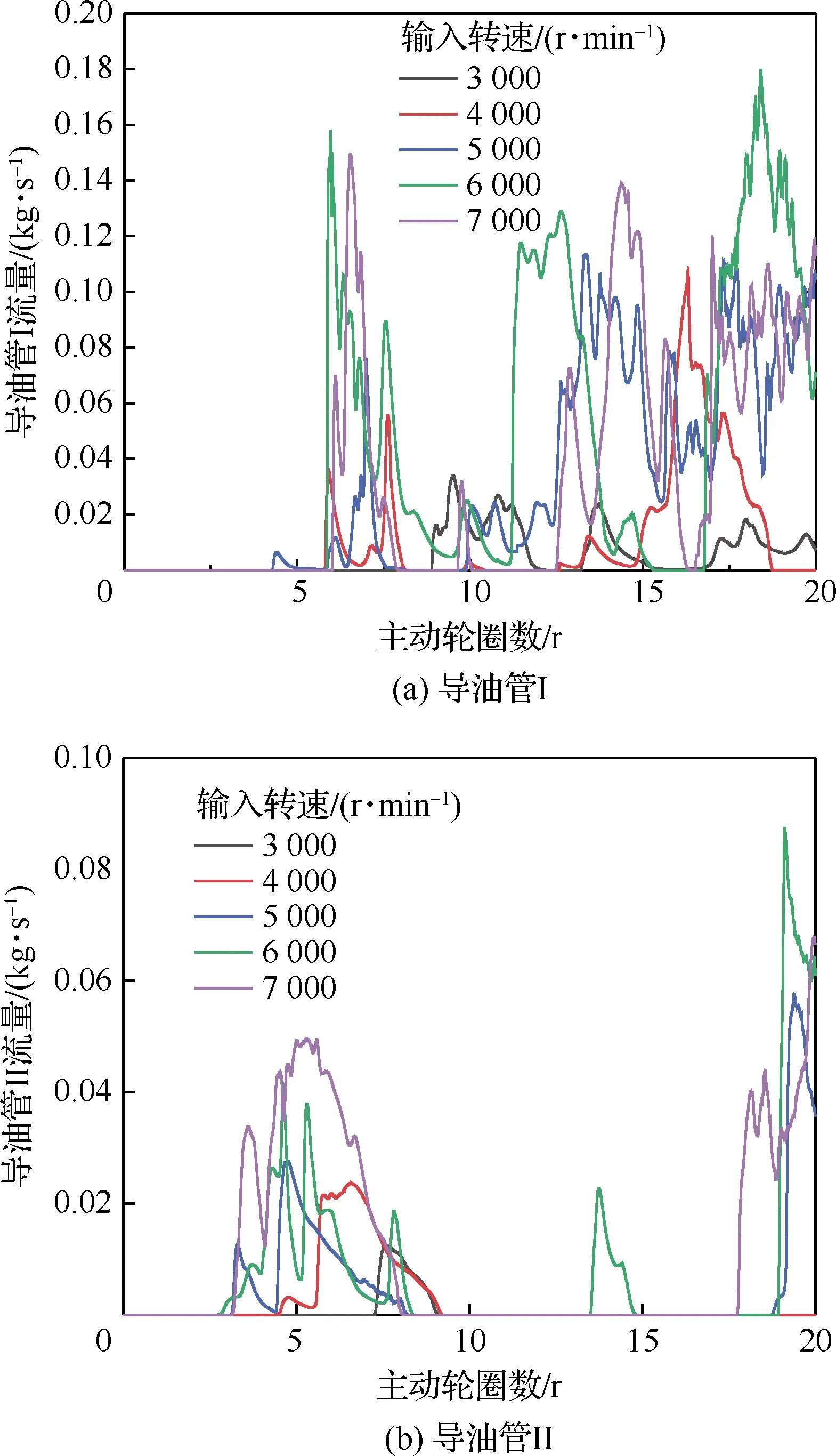
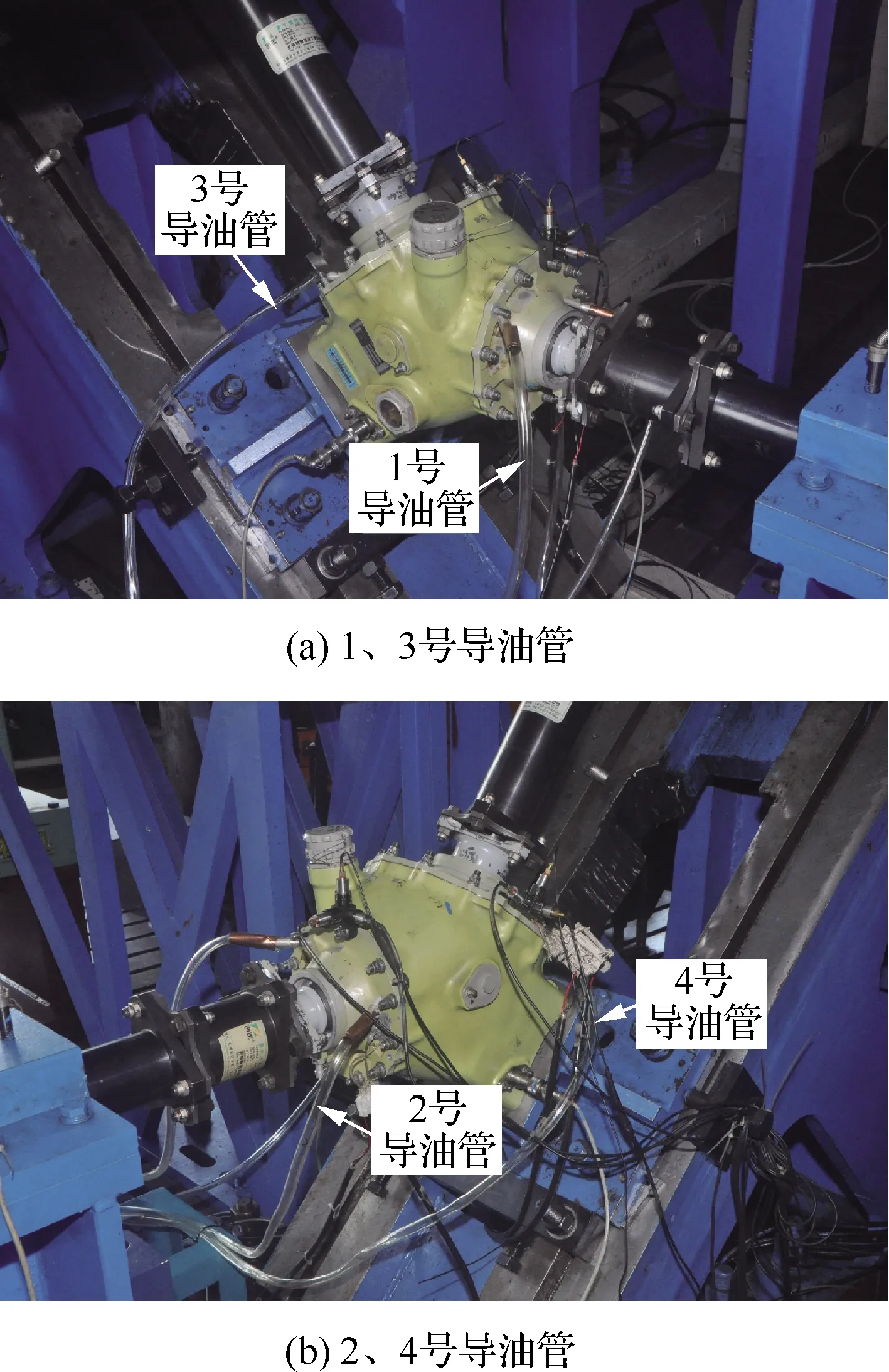
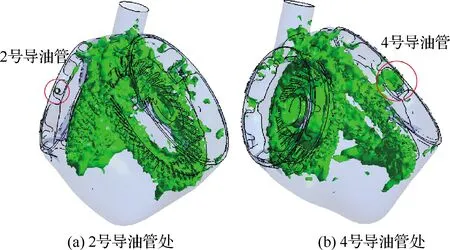
式中:f为流体体积函数,f=0表示该单元中仅含有润滑油,f=1表示该单元中仅含有空气,0 图8 VOF示意图Fig.8 Illustrative diagram of VOF 用R表示主动轮旋转圈数,图9(a)~图9(d)为主动轮旋转5~20 r时的中减飞溅润滑油-气两相流分布。当主动轮旋转5 r时,机匣内壁已附着一定润滑油,且从动轮侧机匣上壁的润滑油明显多于主动轮侧,这是因为初始阶段仅有主动轮浸入润滑油,且主动轮的切向速度包含指向从动轮的分量,使得润滑油首先被飞溅至从动轮侧的机匣内壁上,此时齿轮啮合处润滑油含量少,润滑性能不佳;当主动轮旋转10 r时,机匣上壁已较为均匀地附着有润滑油,且由于齿轮的高速搅动作用,润滑油在机匣底部产生“隆起”,此时齿轮啮合处润滑油量仍较少,润滑性能不佳;当主动轮旋转15 r时,机匣上壁的润滑油含量减少,一部分润滑油受到重力与离心力作用不断流入导油管中,一部分润滑油下落至齿面上,并且由于齿轮高速旋转,机匣内部的压强处于动态变化中,底部的压强高于齿轮啮合处,底部的“隆起”在压力的作用下向齿轮啮合处移动,此时润滑性能良好;当主动轮旋转20 r时,机匣四周已经全部附着有润滑油,底部的“隆起”被齿轮的搅动变得较为分散,齿轮啮合处含有大量的润滑油,此时润滑性能较好。 图9 中减内部油-气两相流分布Fig.9 Two-phase flow distribution of oil and gas in intermediate gearbox 图10为主动轮旋转20 r时齿面油-气两相分布。可以看出,齿面润滑油分布主要集中在啮合区,齿轮轮辐上的润滑油较多。 图10 齿面油-气两相分布Fig.10 Two-phase flow distribution of oil and gas on gear face 图11为主动轮旋转20 r时中减机匣内部的速度流线分布。可以看出,从动轮右侧流线较为密集,因为从动轮侧导油管空气回流现象严重,而主动轮侧几乎没有空气回流现象,因此造成从动轮右侧的速度流线较机匣其他区域更为密集。 图11 中减速度流线Fig.11 Velocity streamline in intermediate gearbox 控制输入转速为5 000 r/min,分析浸油深度(从主动轮最下端计算)分别为8、17、26、35、44 mm 时齿轮与轴承(通过导油管流量间接体现)的润滑效果,确定浸油深度的最佳数值范围。 4.1.1 螺旋锥齿轮齿面润滑状态 齿面润滑油体积分数随浸油深度的变化规律如图12所示。可见,随着浸油深度的增加,齿面润滑油体积分数增加。然而,在保证齿面良好润滑的前提下,应尽量降低齿轮的浸油深度,主要原因如下:① 当浸油深度增加时,润滑油重量会增大,不满足直升机的高功重比要求;② 当浸油深度增加时,齿轮的搅油功率损失增加,润滑油温度会升高引起黏度降低,齿面的油膜易被破坏,导致齿面发生胶合;③ 中减工作过程中,机匣会产生倾斜姿态,若浸油深度过大会导致润滑油浸入轴承内部,加剧轴承的搅油功率损失。 图12 不同浸油深度下的齿面润滑油体积分数Fig.12 Gear oil volume fraction with different oil immersion depths 4.1.2 导油管流量 在Fluent仿真计算过程中监测导油管的流量。不同浸油深度下导油管I和II的流量分布如图13所示。可见,流量曲线波动较大。由图13(a)可知,浸油深度在44 mm以下时,浸油深度越大,润滑油越早流入导油管I;由图13(b)可知,不同浸油深度下导油管II的润滑油分布没有规律,这是因为从动轮倾斜放置,润滑主要靠飞溅至机匣内壁上的润滑油流入。 图13 不同浸油深度下的导油管润滑油流量Fig.13 Oil flow rate of oil guide tubes with different oil immersion depths 4.1.3 导油管润滑油体积 对导油管流量曲线进行数值积分可得导油管润滑油的体积。导油管润滑油体积随浸油深度的变化规律如图14所示,可见润滑油体积随着浸油深度的增大而增加,导油管I中的润滑油体积大于导油管II中的润滑油体积。同时可以发现,浸油深度从17 mm增加至26 mm时,导油管II中的润滑油体积上升趋势明显;然而当浸油深度从26 mm增加至35 mm时,导油管II中的润滑油体积仅增加1 mL,此时润滑效果优化不明显。 图14 不同浸油深度下的导油管润滑油体积Fig.14 Oil volume of oil guide tubes with different oil immersion depths 综合齿面的润滑效果与导油管润滑油的体积变化规律,建议中减浸油深度取17 ~26 mm。 控制浸油深度为17 mm,分析输入转速分别为3 000、4 000、5 000、6 000、7 000 r/min时齿轮与轴承(通过导油管流量间接体现)的润滑效果,进而确定最佳参数范围。 4.2.1 螺旋锥齿轮齿面润滑状态 齿面润滑油体积分数随输入转速的变化规律如图15所示。可见,在3 000~4 000 r/min范围内,齿面的润滑油体积分数较低,此时采用飞溅油润滑方式不能满足润滑要求;在4 000~6 000 r/min 范围内,随着转速的增加,齿面润滑油体积分数增加;然而转速继续上升时,齿面润滑油体积分数下降,这是因为转速过高会导致齿轮对油液的飞溅作用过强,大部分润滑油会被甩至机匣内壁,对齿面的润滑效果反而下降。因此,在确定输入转速时,需考虑齿面润滑效果。 图15 不同输入转速下的齿面润滑油体积分数Fig.15 Gear oil volume fraction with different rotational speeds 4.2.2 导油管流量 不同转速下导油管I和II的流量分布如图16 所示,由于浸油深度相同,即中减机匣内部的润滑油含量相同,在不同转速下,导油管I几乎集中在主动轮旋转6 r左右时开始出现润滑油,导油管II几乎集中在主动轮旋转3 r左右时开始出现润滑油;而由于润滑油的流速不同,导致导油管流量不同。 图16 不同输入转速下的导油管润滑油流量Fig.16 Oil flow rate of oil guide tubes with different rotational speeds 4.2.3 导油管润滑油体积 对导油管流量曲线进行数值积分可得导油管润滑油的体积,导油管内部的润滑油体积随输入转速的变化规律如图17所示。可见,在6 000 r/min 以下,导油管I中的润滑油体积随着转速的增大而增加;而在此之后随着转速的继续增加,润滑油体积反而下降,这是因为齿轮旋转过快,机匣内部气压过低,导油管I处的空气回流现象严重;导油管II中的润滑油体积随着转速的增大而增加。 综合齿面润滑效果与导油管润滑油体积变化规律,建议中减螺旋锥齿轮输入转速为4 000~6 000 r/min。 图17 不同输入转速下的导油管润滑油体积Fig.17 Oil volume of oil guide tubes with different rotational speeds 为了验证CFD方法仿真计算导油管润滑油流量的可行性,在直升机中间减速器传动试验台上开展流场试验,如图18所示。润滑方式为飞溅润滑,试验齿轮箱初始状态下的浸油深度(从主动轮最下端计算)为与仿真相同的17 mm。试验螺旋锥齿轮参数与表1相同,试验油温与仿真油温相同,即60 ℃。试验时,启动电机使主动轮的转速逐渐达到5 000 r/min并稳定运行,通过管接头与两个端盖上的导油管相接,收集4个导油管处的润滑油。 图18 中减传动试验台Fig.18 Intermediate gearbox transmission test-rig 中间减速器平稳运行3 min,导油管流出的润滑油通过量杯收集,如图19所示。4个量杯具体收集到的润滑油体积分别为60、250、28、0 mL,收集油量顺序为2号>1号>3号>4号,可知导油管I的润滑油收集量大于导油管II,并且4号导油管几乎收集不到润滑油,此导油管的结构需要适当改进。 图19 收集到的润滑油Fig.19 Collected lubrication oil 图20为CFD仿真计算导油管处的流量分布。可见,2号导油管流量曲线位于最上方,且曲线仍有增加的趋势,润滑油流量最大;1号导油管位于3号导油管的上方,1号导油管润滑油流量大于3号导油管;4号导油管流量曲线只在初始阶段有数值。由此可以得到仿真计算得到的润滑油流量为2号>1号>3号>4号,趋势与试验所得结果一致。 图20 CFD仿真结果Fig.20 CFD simulation results 图21为仿真得到的机匣内流体涡核图,涡核即为旋涡内部的涡量(速度场的旋度)密集区。可知在螺旋锥齿轮附近出现了较大尺度的涡旋现象,这是由齿轮高速旋转造成的。由图21(a)可知,2号导油管处没有涡旋现象;由图21(b)可知,4号导油管处的涡旋现象极为强烈,产生了较大的速度湍动能。这亦解释了从2号导油管处流入润滑油较为顺畅,而4号导油管处几乎收集不到润滑油的现象,与试验结果(图19)一致。 图21 涡核区Fig.21 Vortex core regions 1) 建立了直升机中减飞溅润滑CFD数值仿真计算模型,得到了机匣内部流体两相流分布,获知主动轮旋转20 r时,齿轮润滑效果良好。 2) 齿面润滑油体积分数随着浸油深度的增加而增加,随着主动轮转速的增加呈现先增加后下降的趋势。 3) 导油管处的流量分布无一定规律,与齿轮浸油深度及转速未呈现正相关趋势。 4) 建议某型直升机中减飞溅润滑浸油深度为17~26 mm,输入转速为4 000~6 000 r/min。 5) 在直升机中间减速器传动试验台上开展流场试验,试验测得的4个导油管润滑油流量趋势与CFD仿真计算结果一致,且有一个导油管收集不到润滑油,说明该导油管的结构需要适当改进。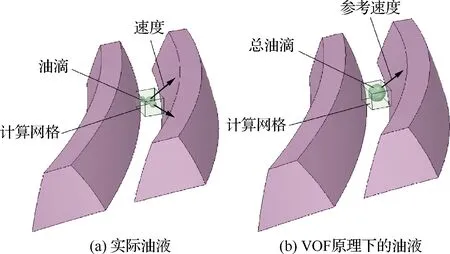
3 中减飞溅润滑数值计算
3.1 中减流场两相流分布

3.2 齿面油气两相分布

3.3 中减流场速度流线分布
4 中减飞溅润滑参数优化
4.1 浸油深度对中减润滑性能的影响
4.2 输入转速对中减润滑性能的影响

5 中减飞溅润滑流场试验验证
5.1 流场试验测试

5.2 试验测试与仿真计算结果对比

5.3 试验结果分析
6 结 论
