基于变式教学理念下的课例与反思

丁叶谦

一、学情分析

本课之前，学生已基本掌握了一次函数的图像和性質，并且可以根据函数图像上点的坐标，利用待定系数法求一次函数图像的解析式，且能利用函数解析式求一些特殊点的坐标，并且在之前方程的学习过程中已经能够利用方程解决行程问题。但利用函数图像以及方程思想综合分析行程问题，学生的能力还略显不足，尤其是解较为复杂的函数图像与行程问题结合的综合题。

二、教学实录与反思

1.问题初探，积累经验。

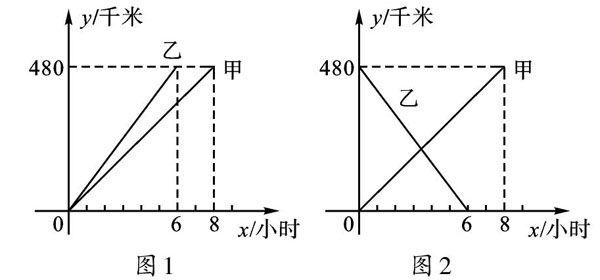
问题1 甲、乙两人分别从相距480千米的A、B两地同时出发相向而行，驶往对方所在地，如图1是他们行驶的路程y（千米）与行驶的时间x（小时）之间的函数图像。从图像中，你能获得哪些信息？

学生1：由点（6，480）可知乙6小时行驶了480千米，所以乙的速度为80千米/小时。

学生2：利用待定系数法可求出y_乙=80x，y_甲=60x。

教师：如果深入分析，你能求出甲、乙相遇的时间吗？

学生3：由题意，可得y_甲+y_乙=480，即80x+60x=480，x=24/7，所以他们经过24/7小时相遇。

变式1 在问题1中，如果甲、乙行驶的速度不变，将y（千米）表示为甲、乙离A地的距离，x（小时）表示他们行驶的时间，你能画出相应的函数图像吗？

学生小组交流展示，画出相应的函数图像，如图2。

教师：哪位同学来分享一下你画出这个函数图像的经验呢？

学生4：我画这个函数图像时主要抓住4个点，即甲的起点和终点、乙的起点和终点，根据y（千米）表示为甲、乙离A地的距离，x（小时）表示他们行驶的时间，可知甲的起点为（0，0）、终点为（8，480），乙的起点为（0，480）、终点为（6，0），分别连接甲、乙的起点和终点便可得出相应的函数图像。

教师：根据画出的函数图像，我们可以发现两条线段明显有一个交点，你能说出这个交点所代表的实际意义吗？

学生5：这个交点表示甲、乙两人行驶一定时间后相遇了。

教师：同问题1一样，你能求出他们相遇的时间吗？

学生6：可以应用待定系数法求出他们的函数表达式：y_甲=60x、y_乙=480-80x。由于y表示他们离A地的距离，当他们相遇时，他们离A地的距离相等，因此y_甲=y_乙，故60x=480-80x，解得x=24/7，所以他们行驶24/7小时相遇。

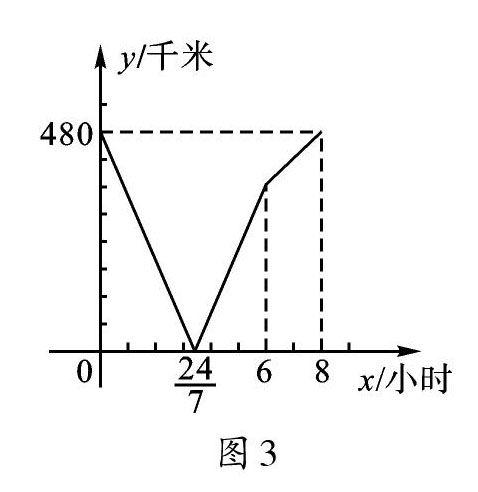
变式2 在问题1中，如果甲、乙行驶的速度不变，将y（千米）表示为甲、乙两人间的距离，x（小时）表示他们行驶的时间，你还能画出相应的函数图像吗？

学生小组交流展示，画出相应的函数图像，如图3。

教师：哪位同学来分享一下你画出这个函数图像的经验呢？

学生7：我在画这个函数图像时主要是先确定几个关键点，然后通过这几个关键点来确定函数图像：首先，由于y（千米）表示为甲、乙两人间的距离，x（小时）表示他们行驶的时间，因此出发前的点坐标为（0，480）;其次是相遇点，相遇时他们之间的距离为0，因此相遇点为（24/7，0）;再次，当乙到达A时，点坐标为（6，360）;最后，甲到达B时，点坐标为（8，480）。将这些点用线段连接便可得函数图像。

教师：通过问题1及变式1、变式2的学习，我们可以发现问题的主题干基本没变，但坐标轴所代表的意义发生了改变，导致函数图像也发生了较大的变化，据此你能获得什么样的学习经验？

学生8：坐标轴所代表的实际意义不同，函数图像便不同，因此在解决此类问题时，我们要关注横、纵坐标所代表的实际意义，同时还需要关注一些关键点。

教师：解决一次函数中的行程问题，我们需要：①弄清横、纵坐标轴所代表的意义;②弄清关键点所代表的实际意义。

【教学反思】问题初探环节是教师在问题1的基础上，借助变式教学，让学生发现同样的问题情境，只是由于坐标轴所代表的意义发生了变化，函数图像也会发生变化，从而突出“核心知识”——横、纵坐标所代表的实际意义，加深学生对“核心知识”的理解，积累学习经验——解决一次函数中的行程问题要弄清横、纵坐标所代表的实际意义，为后续的深入学习打下坚实的基础。

2.变式拓展，提升经验。

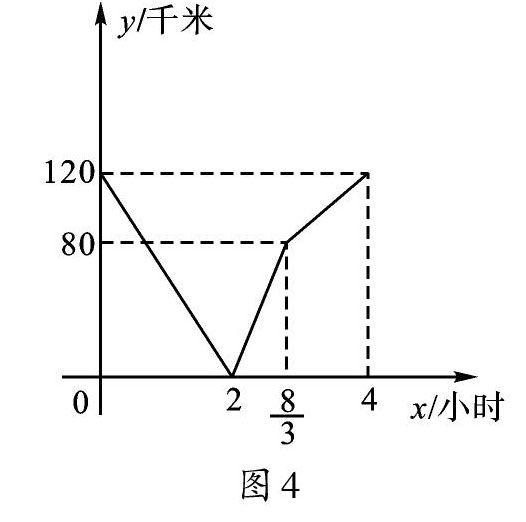
变式3 甲、乙两人从相距120千米的A、B两地同时同向出发，往C地方向前行。甲驾车，乙骑行。当甲追上乙后，将一重要文件交予乙，并立即返回曰处。乙继续骑行到达C地。如图4是他们行驶过程中的函数图像，其中y（千米）表示甲、乙两人的距离，x（小时）表示他们行驶的时间。你能根据图像得到哪些信息呢？

教师：变式3与变式2有何不同？

学生9：本题与变式2相比，坐标轴所代表的意义以及函数图像的形状基本没变，只是数据上稍有变化，但他们的运动方式却发生了变化，变式2中他们是相向运动，而变式3中他们是同向运动。

教师：由此可见，同样的图像，表达的意义却发生了较大的变化，这主要归结于物体运动的方式发生了较大的变化，因此我们在审题时还需要关注物体运动的方式。

教师：那么结合图像，你能获得哪些信息呢？

学生10：结合题意及坐标轴所代表的实际意义，由点（0，120）可知A、B两地相距120千米。

学生11：由点（2，0）我发现甲追上乙用了2小时，画线段图表示为如图5。由点（8/3，80），可知甲从两人相遇处回B地，用时8/3-2=2/3小时，此时甲、乙相距80千米，线段图表示为如图6。由点（4，120），再结合点（8/3，80），可知乙又用4-8/3=4/3小时走了40千米到达C地，因此乙的速度为30千米/小时，B、C两地相距120千米。

学生12：因为甲2小时追上乙，因此甲2小时行驶了120+2×30=180千米，故甲的速度为90千米/小时。

教师：通过以上学习，同学们有何学习经验要与大家交流？

学生13：我觉得解决一次函数中的行程问题，可以从两个方面入手：审题干，弄清物体运动的方式，弄清横、纵坐标轴所代表的意义;审图，弄清图像的归属，弄清关键点所代表的实际意义。

【教学反思】变式拓展环节是教师通过变式3的教学，让学生发现，虽然坐标轴所代表的意义没有发生变化、函数图像没有发生变化，但由于物体运动的方式发生了变化，函数图像所反映出的实际意义也会发生较大的变化，拓宽了学生的认知，突出了核心知识——物体运动的方式、关键点所代表的实际意义，从而使学生初步形成解决一次函数中的行程问题的基本数学活动经验，即要关注物体运动的方式、关键点所代表的实际意义。

3.拓宽提升，形成方法。

变式4 在变式3的基础上，如果只将图4中的4小时删去，其他条件不变，如图7，你能求出甲、乙的速度吗？

教师：通过变式4的学习，你又有什么样的学习经验要与大家分享呢？

学生15：我们在解决一次函数中的行程问题时，有时需要借助画线段图来进行综合分析，有时还需要利用方程思想来解决问题。

教师：通过这堂课的学习，你对解决一次函数中的行程问题有何看法？

学生交流研讨，教师总结板书，给出解决一次函数中的行程问题的基本策略。

【教学反思】教师通过变式4的教学，让学生更加全面、深刻地看到解决此类问题的全貌，形成解决此类问题的基本策略，为学生今后解决一次函数中的行程问题积累经验，提升学生分析和解决此类问题的能力。

纵观以上教学过程，教师是根据学生的学情把握好教学的逻辑起点，采用变式教学的策略，突出解决问题的核心方法，教学设计由浅入深，环环相扣，让学生经历直观、推理、类比、归纳、概括等思维过程，使学生的思维品质得到进一步的提高。