基于AGA8和AGA10的天然气物性参数计算的软件设计
2020-11-30陈玉洁沈昱明
陈玉洁 沈昱明
摘 要: 根据美国燃气协会(AGA)发表的AGA No.8及AGA No.10报告中提出的计算方程,采用向量法、机械求积法等对AGA推荐算法进行了优化;并通过MATLAB编程,计算了天然气物性参数,包括:压缩性系数、比热、声速、等熵指数、焓和熵;分析了AGA8中天然气压缩性系数随压力与温度的变化关系。测试结果表明,计算误差低于0.0003‰,优化后程序运行平均耗时仅150 ms左右。
关键词: MATLAB;天然气;物性参数;AGA8-92DC方程;AGA10;优化算法
中图分类号: TP391.75 文献标识码: A DOI:10.3969/j.issn.1003-6970.2020.09.027
本文著录格式:陈玉洁,沈昱明. 基于AGA8和AGA10的天然气物性参数计算的软件设计[J]. 软件,2020,41(09):9699+132
【Abstract】: According to the calculation equations proposed in the AGA No. 8 and AGA No. 10 reports issued by the American Gas Association (AGA), the AGA recommendation algorithm was optimized using the vector method and the mechanical quadrature method; and the physical properties of natural gas was calculated through MATLAB, including compressibility factor, heat capacity, speed of sound, isentropic index, enthalpy and entropy; the relationship between the compressibility factor of natural gas in AGA8 and the pressure and temperature was analyzed. The test results show that the calculation error is less than 0.0003‰, and the average running time of the optimized program is only about 150 ms.
【Key words】: MATLAB; Natural gas; Physical properties; AGA8-92DC equation; AGA10; Optimization
0 引言
天然氣物性参数,特别是压缩性系数的精确度,对天然气流量计量影响巨大[1]。对于实际气体,常采用PV=ZnRT来代替理想气体状态方程。通过引入压缩性系数Z,以衡量实际气体相对理想气体的偏离程度。
目前,压缩性系数的计算方法有RK公式、Redlieh- Kwong对比态方程[2]、SGERC-88方程、AGA8-92DC方程等。已有大量实验证实了AGA8-92DC方程的精确性,因此在行业中被广泛采用。
文献3、4、5实现了对压缩性系数的编程计算,但计算结果与AGA8所给结果存在较大误差;文献6探讨了AGA8-92DC方程计算值与实验值的差异;文献7基于AGA8-92DC的状态方程,提出了一种简便、准确的计算天然气临界流质量流量的方法。
AGA10虽然给出了计算其他物性参数的算法及源代码,但其算法复杂、代码量大,不利于芯片化运行。本文在其基础上进行了拓展,增加求解了天然气其他重要的物性参数;优化了AGA8、AGA10中的几个偏微分的算法。计算结果与AGA8、AGA10中的结果完全吻合,也大大缩短了计算时间。经测试,平均计算时间约为150 ms。
1 AGA8-92DC方程及其计算精度
在1992年6月召开的国际标准化组织(ISO)上,美国燃气协会(AGA)提出了计算天然气压缩性系数的AGA8-92DC方程(以下简称AGA8方程)。AGA8方程是参照天然气组分摩尔分数来计算的扩展维里方程。在甲烷含量不低于70%,温度263 K~338 K,绝对压力低于20 MPa的工作条件下,计算不确定度优于± 0.2%,能满足绝大部分的工业条件。
2 优化计算
输入变量为21种天然气组分的摩尔分数、温度及绝对压力,MATLAB软件编程计算后,输出天然气物性参数值,包括压缩因子、比热、声速、等熵指数、焓和熵。其中,比热、声速、等熵指数、焓、熵的计算公式参照AGA No.10报告[8]。
计算输入常量说明如下,详见GB/T17747.2-1999[9]表B.1、表B.2、表B.3和表4:
——状态方程参数,n=1~58
——天然气组分特征参数
——二元交互作用参数
——比热、焓和熵的计算参数
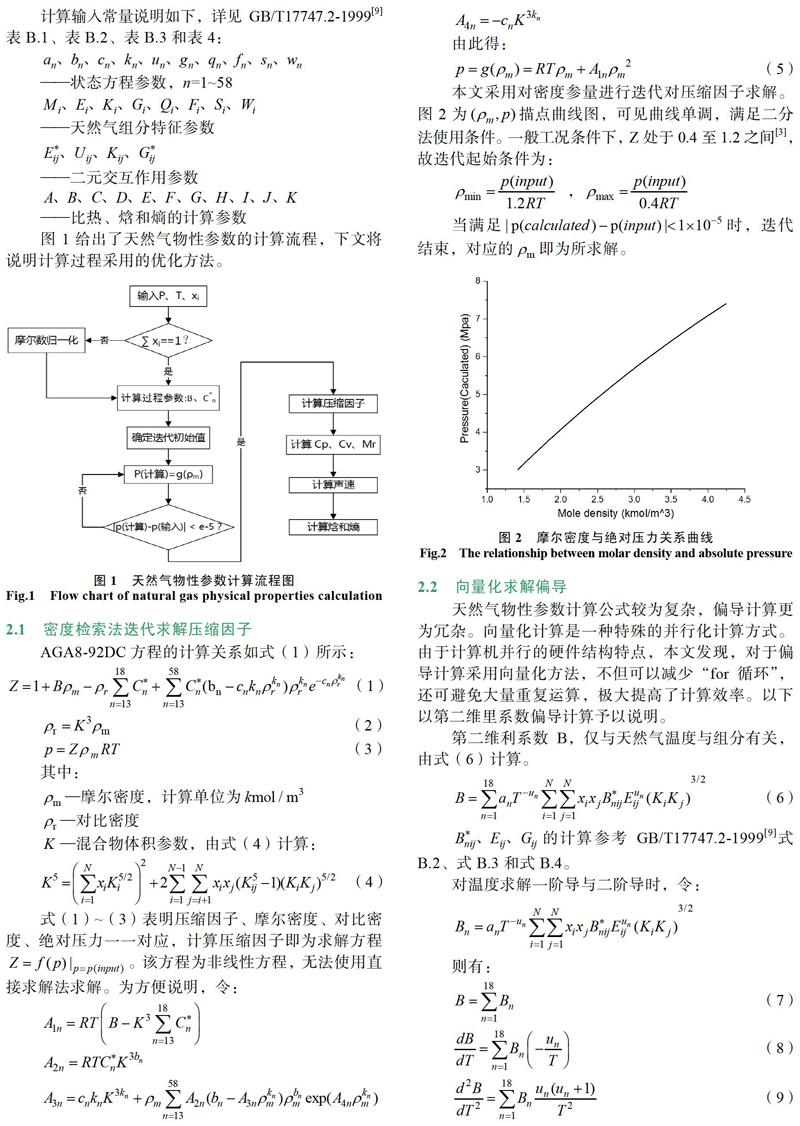
图1给出了天然气物性参数的计算流程,下文将说明计算过程采用的优化方法。
2.1 密度检索法迭代求解压缩因子
AGA8-92DC方程的计算关系如式(1)所示:
式(1)~(3)表明压缩因子、摩尔密度、对比密度、绝对压力一一对应,计算压缩因子即为求解方程。该方程为非线性方程,无法使用直接求解法求解。为方便说明,令:
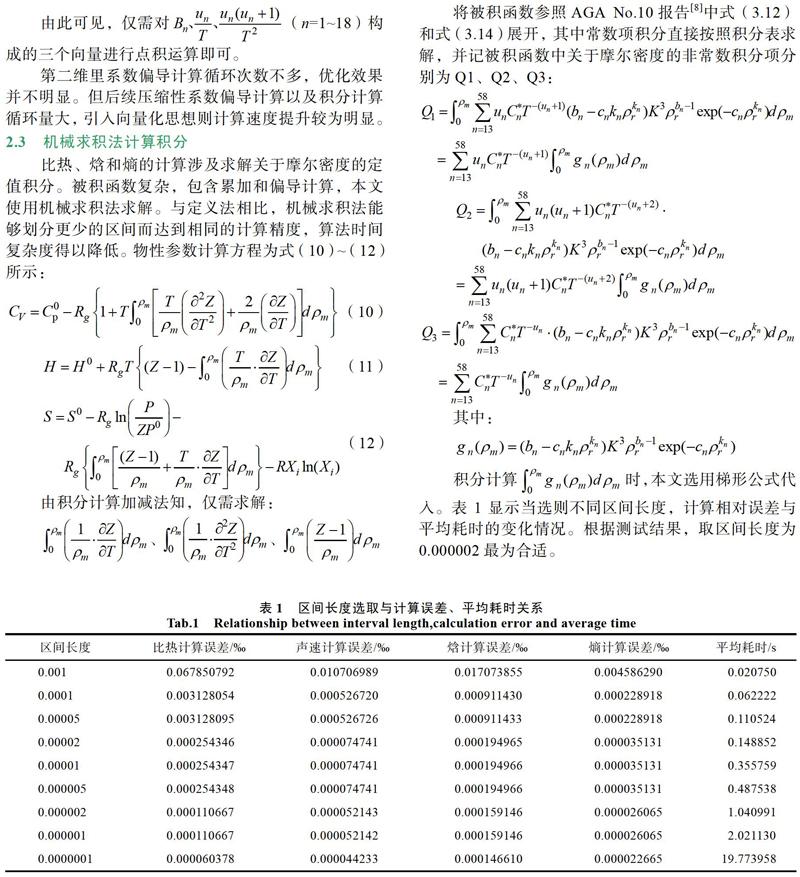
本文采用对密度参量进行迭代对压缩因子求解。图2为描点曲线图,可见曲线单调,满足二分法使用条件。一般工况条件下,Z处于0.4至1.2之间[3],故迭代起始条件为:
当满足时,迭代结束,对应的即为所求解。
2.2 向量化求解偏导
天然气物性参数计算公式较为复杂,偏导计算更为冗杂。向量化计算是一种特殊的并行化计算方式。由于计算机并行的硬件结构特点,本文发现,对于偏导计算采用向量化方法,不但可以减少“for循环”,还可避免大量重复运算,极大提高了计算效率。以下以第二维里系数偏导计算予以说明。
第二维利系数B,仅与天然气温度与组分有关,由式(6)计算。
由此可见,仅需对(n=1~18)构成的三个向量进行点积运算即可。
第二维里系数偏导计算循环次数不多,优化效果并不明显。但后续压缩性系数偏导计算以及积分计算循环量大,引入向量化思想则计算速度提升较为明显。
2.3 机械求积法计算积分
比热、焓和熵的计算涉及求解关于摩尔密度的定值积分。被积函数复杂,包含累加和偏导计算,本文使用机械求积法求解。与定义法相比,机械求积法能够划分更少的区间而达到相同的计算精度,算法时间复杂度得以降低。物性参数计算方程为式(10)~(12)所示:
将被积函数参照AGA No.10报告[8]中式(3.12)和式(3.14)展开,其中常数项积分直接按照积分表求解,并记被积函数中关于摩尔密度的非常数积分项分别为Q1、Q2、Q3:
积分计算时,本文选用梯形公式代入。表1显示当选则不同区间长度,计算相对误差与平均耗时的变化情况。根据测试结果,取区间长度为0.000002最为合适。
3 软件设计
GUI(Graphical User Interface),指利用图形控件进行人机交互操作。为了方便用户的使用,本文引入MATLAB的GUI技术[10],只需用户在人机交互界面上输入天然气温度、压力和组分摩尔数,即可自行计算出物性参数。
图形界面设计完成后,通过Matlab的自动导出功能可将计算程序*.m文件与GUI图形界面*.fig文件合并为一个.m文件。随后C/C++编译器生成*.exe可执行文件。未安装MATLAB的机器仅需下载编译环境库MATLAB Runtime(MCR)或者将MATLAB安装路径下的/toolbox/compiler/Deploy/win32的MCRInstaller.exe与编译的执行文件打包发送即可,执行文件运行时会自动调用下载的动态链接库DLL。
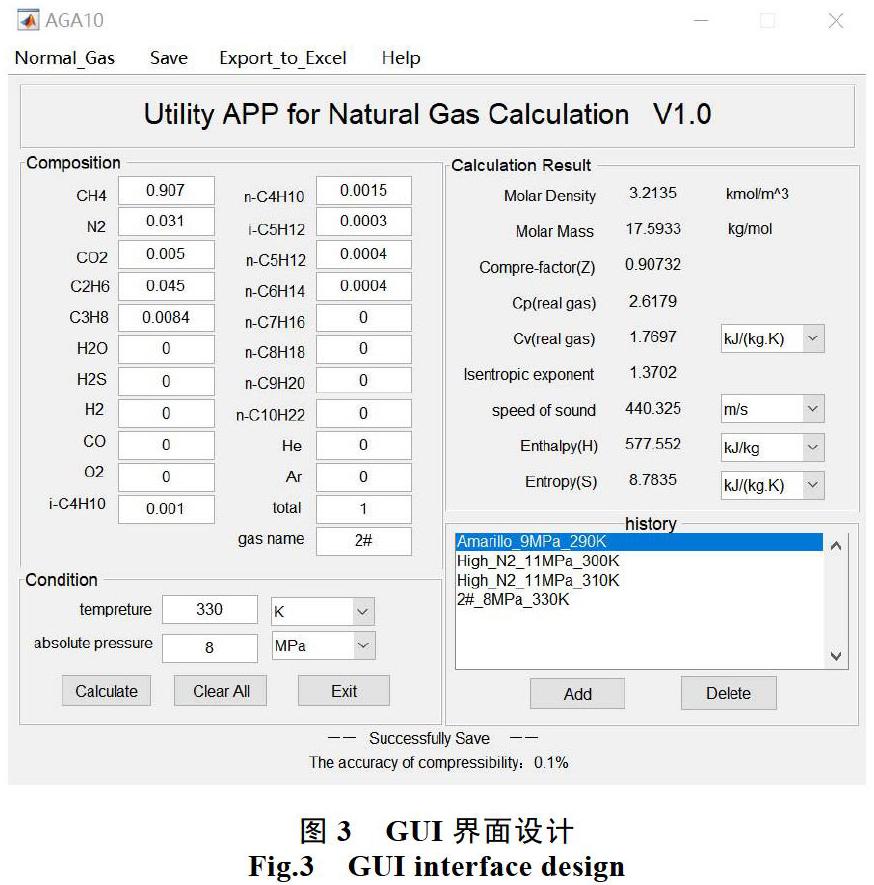
但MCRInstaller.exe所占内存较大,可移植性不高,对应用范围有一定限制。既需MATLAB强大的计算能力,又需生成便捷的计算机软件,也可采用其他编程语言调用MATLAB程序。如Mideva工具编译*.m文件后可生成能被Visual C++[12]、Visual Basic以及Delphi调用的DLL动态链接库。Microsoft VB在软件开发界面上具有独到之处,但在计算方面略显不足,这方面恰可与MATLAB互补[13]。图3是本文软件界面设计。
4 测试
本文将软件计算结果与GB/T 17747-1999与AGA No.10报告中算例进行比较,计算结果中压缩性系数完全一致,其他参数如表1所示,计算相对误差小于0.0003‰,说明软件计算正确,满足精度要求。
MATLAB源程序中,本文利用tic, toc语句对程序进行时间测试。不采用任何优化方法计算(默认使用循环结构和MATLAB自带积分函数),平均耗时为1.5 s;优化后平均耗时为150 ms,降为原来的10%,优化效果明显。
表2中显示的是AGA10更宽的应用范围,本文在AGA8原有数据的基础上,计算了更高温度、更大压力条件的压缩性系数。对于AGA8所展示的6种天然气,其压缩性系数与温度、压力的关系如图4所示。
可以看出:对同一种类天然气,压力为6 MPa的压缩性系数变化曲线与12 MPa情况下相差较大,而12 MPa与20 MPa曲线几乎重合。
5 结语
(1)本文采用向量化方法、机械求积法、密度检索法迭代等优化算法,极大提高了計算效率。
(2)计算结果与AGA报告数据相比,二者完全吻合。
(3)对同一种类天然气,压力为6 MPa的压缩性系数变化曲线与12 MPa情况下相差较大;而12 MPa以上曲线几乎重合;且随温度升高,不同压力下天然气压缩性系数差值减小。
参考文献
[1]孟祥适, 姜印平, 刘玉杰, 等. 基于天然气压缩系数Z提高天然气计量准确度的方法[J]. 测控技术, 2004, 23(6): 16-17, 28.
[2]黄希扬, 沈昱明. 基于Redlieh-Kwong对比态方程的天然气压缩因子计算[J]. 化工自动化及仪表, 2019, 46(02): 107-110.
[3]李丹华, 姜东琪. AGA8-92DC计算方法天然气压缩因子计算[J]. 煤气与热力, 2011, 31(03): 43-46.
[4]梁光川, 左果, 文雯, 等. 应用VB实现AGA8-92DC气体压缩因子计算方法[J]. 辽宁化工, 2014, 43(05): 609-612.
[5]陈旻灏, 黄希扬, 沈昱明. Matlab与LabVIEW混合编程的天然气压缩因子软件设计[J]. 化工自动化及仪表, 2019, 46(10): 844-848.
[6]苏中良, 刘曰武, 张俊清. AGA8-92DC方法计算天然气偏差因子的研究[J]. 油气井测试, 2010, 19(06): 29-36+83.
[7]D.G. Stewart, J.T.R. Watson, A.M. Vaidya. A new correlation for the critical mass flux of natural gas mixtures[J]. Flow Measurement and Instrumentation, 2000, 11(4).
[8]AGA Report No. 10 Speed of Sound in Natural Gas and Other Related Hydrocarbon Gases[S]. Transmission Measurement Committee. 2002.11.15.
[9]GB/T 17747.2-2011, 天然气压缩因子计算—第2部分: 用摩尔组成进行计算(ISO 12213-2:2006)[S]. 2011, 12, 30.
[10]姚楠, 耿奇. 基于MATLAB GUI的车牌自动识别系统设计[J]. 软件, 2016, 37(3): 44-46.
[11]曹妍, 陈伟. 基于MATLAB GUI的指纹图像增强技术研究[J]. 软件, 2018, 39(11): 30-32.
[12]徐治. Visual C++调用MATLAB函数库的混合编程技术[J]. 软件, 2015, 36(2): 55-58.
[13]曹妍, 陈伟. 基于MATLAB图像处理的药片计数方法研究[J]. 软件, 2018, 39(9): 13-15.
[14]刘艳华. 数字图像置乱加密解密技术的研究与实现[J]. 软件, 2018, 39(3): 141-144.
