耦合双谱运算在语音信号分析中的应用

梅二召 范景峰

摘  要： 为了进一步提取语音信号中的特征信息，采用一种耦合双谱运算的分析方法。在双谱运算中，由于复数三阶累积量的定义方式不同，所包含的耦合信息成分也不同。因此，根据复数三阶累积量的不同定义方式，对实数域内不容易区分的语音信号进行复数域内双谱及其对角切片分析。实验结果表明，根据复数三阶累积量的不同定义进行的双谱及其对角切片谱分析，能够区分出实数域内不易区分出的语音信号，而且由于在不同定义下所包含的耦合信息不同，双谱及其对角切片分析结果也不同。

关键词： 语音信号分析;耦合;复双谱运算;双谱对角切片;复数三阶累积量

中图分类号： TP391.1    文献标识码： A    DOI：10.3969/j.issn.1003-6970.2020.09.003

本文著录格式：梅二召，范景峰. 耦合双谱运算在语音信号分析中的应用[J]. 软件，2020，41（09）：0912+25

【Abstract】： In order to further extract the characteristic information of speech signal， one method of analysis coupled bispectrum operations was proposed. In the bispectrum operations， the complex forms with different definitions of three-order cumulants included different coupling information of signals. Thus， this paper used the complex bispectrum and its diagonal slice to analyze the speech signal which is difficult to distinguish in the real number field depending the complex forms with different definitions of three-order cumulants. The experiment results show that using the complex bispectrum and its diagonal slice can distinguish the speech signal which is difficult to distinguish in the real domain depending the complex forms with different definitions of three-order cumulants， and the complex bispectrum and its diagonal slice analysis results are different since the forms with different definitions included different coupling information of signal.

【Key words】： Speech signal analysis; Coupling; Complex bispectrum operation; Bispectrum diagonal slices; Complex third-order cumulants

0  引言

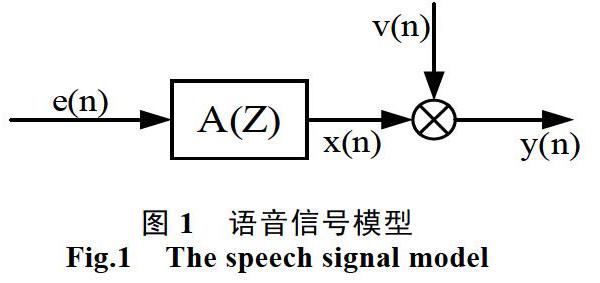
語音信号通常被认为是一个受准周期脉冲或随机噪声源激励的线性系统输出，输出频谱是声道系统频率响应与激励源频谱的乘积[1-2]。文献[3]指出，在短时间内，语音信号模型近似与如图1所示的平稳随机过程的自回归（AR）模型。在图1中，语音信号y（n）是由均值为零的高斯白噪声e（n）激励线性时不变系统A（Z）产生的，v（n）和e（n）统计独立的加性高斯白噪声，线性时不变系统的传输函数A（Z）是最小相位的。利用高阶累积量可以自动抑制高斯背景噪声（有色或白色）的影响，将高阶谱分析技术应用于语音编码中以提高其抗噪声的性能。刘福星、何选森在三阶累积量的语音激活检测方法中指出，在电子与通信系统中，传输信号的噪声都可以看作是加性的高斯随机过程，而高斯随机过程的三阶累积量为零，通信系统中传输的语音信号一般是非高斯信号[4]。因此，采用三阶累积量的方法可以区分语音信号和噪声信号。

根据语音产生的机理，其中存在着非线性相位耦合现象。M.R.Raughveer和国内学者张严、王树勋等人对耦合信息在复数高阶累积量计算中产生的影响进行深入研究，明确给出不同定义方式下耦合信号在三阶累积量和及其对角切片中所占成分的计算公式[6-8]。吴文兵等人把复三阶累积量耦合性质应用在机械故障诊断结果中，得出影响故障诊断结果的不是谱的形式，而是其中包含的不同的耦合信息[9]。因此，利用高阶累计量能够有效地抑制高斯噪声，把耦合双谱运算应用到语音信号分析中，来实现对语音信号的特征提取。

1  复数三阶累积量

在信号处理和系统理论中，很多信号都可被看作是白噪声激励一个线性时不变系统的结果。设输出为零均值的k阶平稳随机过程，则k阶累积量定义为[10，11]：

当k=3时，称为三阶累积量;当时，称为三阶累积量对角对角切片。双谱为三阶累积量的二维傅里叶变换，双谱对角切片即为三阶累积量对角切片的一维傅里叶变换。

当为复数信号，且，其中时，根据文献[8]可知，复数信号三阶累积量根据其各项取共轭与否有8种定义方式。本文选取其中3种定义方式进行分析及应用与语音信号处理中。

式中为的共轭复数，而本文中使用的复数信号是由采样语音信号进行Hilbert变换得到的。由文献[8]可以知道，当谐波分量是由谐波分量和通过二次相位耦合而成的，即时，为耦合信号。根据上述三种定义方式，按照定义一下的三阶累积量和三阶累积量对角切片都为零。定义二和定义三方式下的三阶累积量和三阶累积量对角切片分别为：

由三阶累积量和三阶累积量对角切片可以看出，按照定义一下的双谱及其对角切片谱中不含耦合信息成分;定义二下的三阶累积量中只包含谐波分量和，因此所对应的双谱中也只含有和信息，而式（6）中只含有耦合而成的谐波分量，其对应的双谱对角切片中也只含有;定义三下的三阶累积量中包含所有的谐波分量，其双谱中也保留了各次谐波分量，而式（8）中仅含有谐波分量和，所对应的双谱对角切片中也只含有谐波分量和。

2  数据采集

实验数据采集是基于LabVIEW的声卡语音信号采集系统实现的。在LabVIEW环境中对声卡进行编程，可实现对声卡参数的自由设定，同时利用LabVIEW软件的图形化编程优点，可实现界面风格与传统仪器相似的效果[12-15]。当语音信号输入时，语音信号首先经过信号调理电路，调理电路的作用主要包括信号的放大、滤波、隔离和线性化处理，以使其能够被声卡正确的识别。利用PC机声卡的麦克风输入或线路输入作为信号的输入端口，将获取到的模拟音频信号经过左右两个通道和A/D转换后送入计算机，通过LabVIEW编写的采集程序进行各种处理和保存，其系统框图如图2所示。

根据使用计算机声卡的实际特性，将声卡设置为双通道、44.1 kHz采样频率、16位采样比特数、手动采集，以保证采样时的干扰较小、波形稳定。虚拟示波器主要是对声卡采集音频信号的时域实时显示，后面板程序使用while循环结构实现數据实时显示和数据实时存储，后面板程序设计如图3所示。

实验采集过程是在相对安静的环境中进行，不掺杂外来噪音，实验人员均在语速和缓、心情平稳下录制包含96个字的同一段话，在LabVIEW中通过设置保存路径选择保存的位置，保存格式为WAV文件。使用LabVIEW还有一个优点就是可以通过通过Mathscript节点调用MATLAB程序，从而实现语音信号的后续处理。

3  实验数据分析

为研究耦合信息在复数三阶累积量中对信号识别的影响，对采集到的80组数据进行实数和复数域内分别进行双谱及其对角切线谱分析，并且在复数域内通过改变三阶累计量定义形式来观察不同定义形式下，耦合信息对双谱及其对角切线谱的影响。从实数和复数域内双谱及其对角切线谱图归纳总结，从中选取图4至图6进行分析。

图4中选取的是在实数域内男生和女生语音信号进行双谱及其对角切片谱分析结果图，图4中01、02和05、06是男生语音信号的双谱图及其对角切片图，03、04和07、08是女生语音信号的双谱图及其对角切片图。对比图01（a）和02（a）男生双谱图可以看出，图01（a）男生语音双谱图中有6个峰值较高的谱峰，而双谱图下部有较多小的谱峰，且谱峰表现的较为尖细;图02（a）中只是出现2个峰值较高的谱峰，而双谱图下部出现的谱峰较低，且谱峰表现的较为粗大。与其对应的双谱对角切片图中亦可明显区分出两个男生语音信号的双谱对角切片图的差异。对比图03和图04亦可发现两个女生语音信号的双谱及其对角切片图有明显区别。而综合比较01、02、03和04中两名男生和两名女生语音信号双谱图及其对角切片图可以发现男生语音信号双谱图谱峰分布较为宽广，女生语音信号双谱图谱峰分布较为集中。

对比图05和06可以看到，两个双谱图中都有6个峰值突出的谱峰，且6个谱峰分布位置较为接近，从其对应的对角切片谱中亦可看到两个主峰位置都分布在85Hz附近。对比图07和08亦可看到两女生语音信号的双谱及其对角切片谱也是比较接近。而综合比较05、06、07和08中两名男生和两名女生的双谱及其对角切片谱图亦是较为接近的，从整体上表现的特征不够明显。因此，对这类语音信号，通过Hilbert变换，再根据三阶累计量的不同定义形式对其进行双谱及其对角切片谱再分析。

图5、图6和图7是与图4中05、06、07和08相对应的复数域内按照三阶累计量的定义一、定义二和定义三方式下男生和女生语音信号双谱及其对角切片切线谱图。从图5的双谱及其对角切片谱图中可以看出，图09谱峰较多且较为尖细，其对应的对角切片谱主峰位置在195 Hz处;图10中的有一个峰值最高的主峰，双谱图下部的谱峰较为粗大，与其对应的对角切片谱中的主峰位置在185 Hz处;图11中的双谱图有3个峰值较高的谱峰，其对角切片谱中主峰位置在175 Hz处;图12中的双谱图较为简单只有一个突出的主峰，且其主峰在对角切片图中位置为155 Hz处。综合图5中的两名男生和两名女生的双谱及其对角切片谱较实数域内双谱图更加简洁且谱峰更加清晰。

从图6中的语音信号双谱及其对角切线谱中亦可清晰地区分出这两名男生及女生的语音信号的各自特点。对比图5中按照三阶累积量定义一下的语音信号双谱及其对角切片谱图可以看出，三阶累积量在定义一方式下耦合信号的三阶累积量为零，而定义二方式下含有耦合信息的和成分。从整体上来说，图6双谱图表现的更加集中，而对角切片图中主峰频率值整体上都有所减小。

图7中按照三阶累积量定义三方式下的双谱及其对角切片谱图中可以明确区分出各自语音信号的特点。对比图5的双谱图，双谱图也是较为集中，其对角切片谱中没有像图6中表现的主峰频率值整体减小的现象，但对角切片谱图之间区别亦是较为清晰。

4  结论

根据实验数据分析，可以看出有些语音信号在实数域内就已经很容易区分，对这些信号而言，在实数域内进行双谱及其对角切片谱分析就能达到信号识别的目的。但有些语音信号在实数域内的信号双谱及其对角切片谱图表现的较为相近，不容易区分，为了对这类信号进行识别，对该类信号进行Hilbert变换，对其在复数域内进一步分析。由于复数域内三阶累积量的定义方式不同，信号中的耦合信息在双谱及其对角切片谱图中的所占的成分不同，对此本文选取三种典型的定义方式进行语音信号的分析，而三种定义方式下的三阶累积量所生成的双谱及其对角切片谱图都能清晰地区分出在实数域内不易区分的语音信号，而不同之处就在于由于不同定义方式下耦合信息在信号进行三阶累积量计算中所占的比重不同，使其双谱图中的谱峰分布及其谱峰大小有所区别，但整体而言，复数域内的双谱图表现的更加简洁，谱峰分布更加集中，而其对角切片图中的主峰亦是更加明确。因此，在复数域内采用三阶累积量的不同定义方式对语音信号进行分析，可以实现实数域内较难区分的语音信号在复数域内进行区分。

参考文献

[1]刘星燕， 贾磊， 薛君彦. 浅谈张家口 121 语音答询系统几个常见问题的处理[J]. 软件， 2018， 39（1）： 180-182.

[2]王爱芸. 语音识别技术在智能家居中的应用[J]. 软件， 2015， 36（7）： 104-107.

[3]姚文冰， 姚天任， 韓涛. 高阶谱分析在抗噪语音编码中的应用[J]. 华中科技大学学报， 2001， 29（9）： 60-62.

刘福星， 何选森. 三阶累积量的语音激活检测方法[J]. 计算机工程与应用， 2011， 47（17）： 137-139.

[4]陈亮， 张雄伟. 语音信号非线性特征的研究[J]. 解放军理工大学学报， 2000， 1（2）： 11-17.

[5]M R Raughveer. Time-domain approaches to quadratic phase coupling estimation Automatic Control[G]. 1990. AC 35： 48-56.

[6]张严， 王树勋， 李生红. 二次相位耦合的11/2维谱分析[J]. 电子学报， 1996， 64（04）： 109-112.

[7]张严， 王树勋. 非线性相位耦合的切片谱分析方法[J]. 电子学报， 1998， 26（10）： 104-109.

[8]吴文兵， 梅二召， 欧阳鑫， 李川. 基于复数信号的三阶累积量微分性质研究及应用[J]. 哈尔滨工程大学学报， 2015（08）： 1073-1079.

[9]W. B. Collis， P. R. White， J. K. Hammond. Higher-order Spectra： the Bispectum and Trispectrum[J]. Mechanical Systems and Signal Processing， 1998， 12（3）： 375-394.

[10]Dusan Kocur， Radoslav Stanko. Order Bispectrum： a New Tool for Reciprocated Machine Condition Monitoring[J]. Mech anical Systems and Signal Processing， 2000， 14（6）， 871-890.

[11]皮祖成， 陈文， 戴善溪. 基于LabVIEW面向对象的试车台实验控制软件设计[J]. 软件， 2016， 37（08）： 104-110.

[12]胡武扬， 段富海， 董科锐. 基于LabVIEW 的舵机自动加载测试系统软件设计[J]. 软件， 2015， 36（5）： 24-29.

[13]陈志. 基于LabVIEW的插值校验电路脉冲输出的程序设计[J]. 软件， 2018， 39（10）： 64-67.

[14]李岳， 韩宾， 鲁云. 基于声卡和LabVIEW的声音信号EMD时频分析系统[J]. 微型机与应用， 2016， 07： 73-75+78.