一种迭代的自适应中值滤波算法
2020-11-30马丽圆常锦才
马丽圆 常锦才

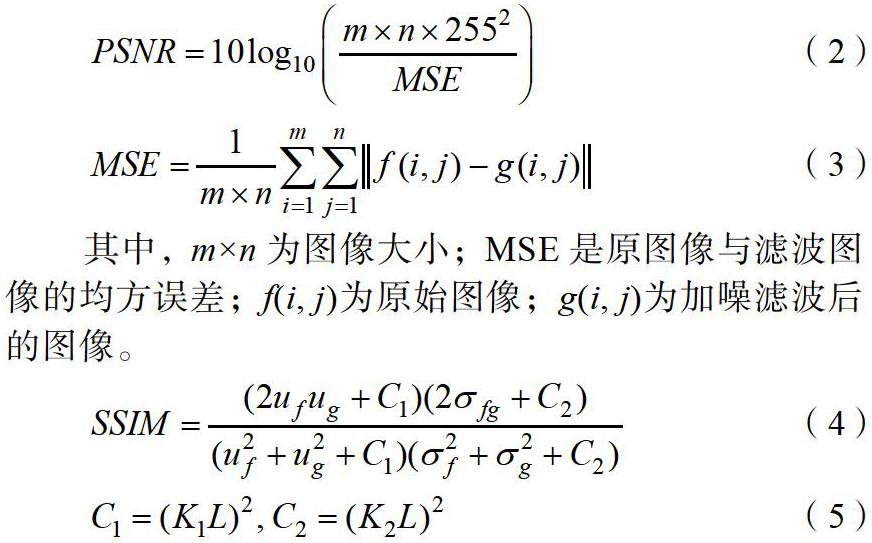
摘 要: 本文针对自适应中值滤波算法对高密度固定值脉冲噪声去噪效果欠佳的缺陷,提出一种扩大窗口时利用上次滤波结果的迭代方法,同时为了提高去噪效果,将最大滤波窗口调整至9×9。通過仿真分析,相比于现有的自适应中值滤波算法,新算法的去噪效果得到明显提高。
关键词: 固定值脉冲噪声;中值滤波;迭代方法
中图分类号: TN911.73 文献标识码: A DOI:10.3969/j.issn.1003-6970.2020.09.019
本文著录格式:马丽圆,常锦才. 一种迭代的自适应中值滤波算法[J]. 软件,2020,41(09):6971
【Abstract】: This paper proposes an iterative method that uses the previous filter results when expanding the window to address the shortcomings of the adaptive median filter algorithm's poor denoising effect on high-density fixed-value impulse noise. At the same time, in order to improve the denoising effect, the maximum filter window is adjusted to 9×9. Through simulation analysis, compared with the existing adaptive median filter algorithm, the denoising effect of the new algorithm has been significantly improved.
【Key words】: Fixed-value impulse noise; Median filtering; Iterative method
0 引言
图像作为现代社会的一种重要的信息来源之一,其在拍摄和处理的过程中经常会产生噪声,导致图像的视觉效果差、信息质量下降。因此,采用合理的方法去除图像噪声[1]尤为重要。脉冲噪声[2]是一种常见的图像噪声,可分为随机值脉冲噪声和固定值脉冲噪声,其中固定值脉冲噪声随机地产生值为0或255的像素点,即产生黑白点;随机值脉冲噪声随机地将灰度值改为介于最大值和最小值之间的随机值。中值滤波算法[3]是滤波算法中经典的去除固定值脉冲噪声的方法,但是由于中值滤波算法将所有像素点均改为领域中值,未将信号像素和噪声像素区分开,并且滤波窗口固定为3×3,使得图像的边缘和细节容易模糊,当噪声密度较高时,去噪效果不明显。因此,又提出了一种自适应的中值滤波算法[4],用领域内的最值来识别噪声像素,对识别出的噪声像素用领域中值替换,取得了较好的效果,但其对于高密度的噪声去噪效果仍然欠佳。此外,很多学者针对中值滤波算法进行研究,并提出了很多改进算法,包括基于改进多级中值滤波的加权滤波算法[5]、改进的自适应加权中值滤波算法[6]等。本文则在自适应中值滤波算法的基础上进行改进,充分利用前次滤波处理后的像素进行迭代[7],同时扩大最大滤波窗口为9×9,明显提高了去噪效果,使得图像的峰值信噪比和与原图的相似性结构得到有效提高,去噪效果优于原本的自适应中值滤波算法。
1 自适应中值滤波算法简介
1.1 算法原理
该算法[8]将噪声像素和信号像素通过窗口最值识别,且滤波窗口[9]范围动态调整。首先计算窗口内的最值和中值,当窗口中值为信号像素时,若当前像素为噪声像素(当前像素为最值),则用中值替换当前像素;若当前像素为信号像素,则不作处理。当窗口中值为噪声像素,不作处理,等待扩大窗口。
1.2 算法特点
对于本身为信号的像素点不作处理,很好地保护了图像的细节和边缘信息;
当窗口中值为噪声像素,则自动扩大窗口,增强处理效果;
对已经处理过的像素值未能很好地利用,当噪声强度过高时,去噪效果欠佳。
2 迭代的自适应中值滤波算法
由于固定值脉冲噪声产生灰度值为0或255的像素点,故通过像素值是否为0或255来区分噪声值和信号值,并且加以标记。对噪声值的像素进行替换,
若当前窗口范围内的中值为信号像素,则用其替换该噪声像素,否则不处理。当所有可遍历[10]像素点在该窗口大小下均被遍历完之后,扩大窗口大小,重新计算原像素在替换后的新像素分布的中值,继续处理,直到达到最大滤波窗口(9×9)后终止。之后将剩余的噪声像素用处理后的像素在3×3滤波窗口下的中值替换。具体操作步骤如下:
Step 1:遍历所有像素f,通过像素值是否为0或255,将噪声像素值和信号像素值区分开来,并将其用矩阵isTrue标记,令滤波窗口k=3。
Step 2:对isTrue(r,c)=0的f(r,c),用matlab中medfilt2()函数计算k×k窗口内f的滤波中值zmed(r,c),如果zmed(r,c)不是噪声像素,则将f(r,c)的值用zmed(r,c)的值替换,并将isTrue(r,c)更改为1;否则,不作处理。
Step 3:若k≤9,则k=k+2,转Step 2;否则,继续Step 4。
Step 4:此时图像像素值已在最大滤波窗口下遍历完毕,对于剩余的isTrue=0的像素点,用3×3窗口的f的滤波中值替换。
3 仿真结果及数值分析
下面对本文提出的改进算法进行仿真实验,给512×512图像Lena添加不同密度的脉冲噪声,对其进行滤波处理,与自适应的中值滤波算法结果进行对比,分析二者的处理效果。数据分析时引入峰值信噪比(PSNR)[11]-[12]和图像相似性结构(SSIM)[13]作为评价标注。PSNR和SSIM的表达式具体如下。
其中,m×n为图像大小;MSE是原图像与滤波图像的均方误差;f(i, j)为原始图像;g(i, j)为加噪滤波后的图像。
其中,uf和ug分别代表图像f和g的均值;σf和σg分别代表图像f和g的标准差;σfg代表图像f和g的协方差[14];C1和C2为平衡常数;L=255;K1和K2取默认值0.01和0.03。对原图像添加密度为0.8的噪声,分别用自适应中值滤波和改进的新算法进行滤波去噪,仿真效果图如图1。
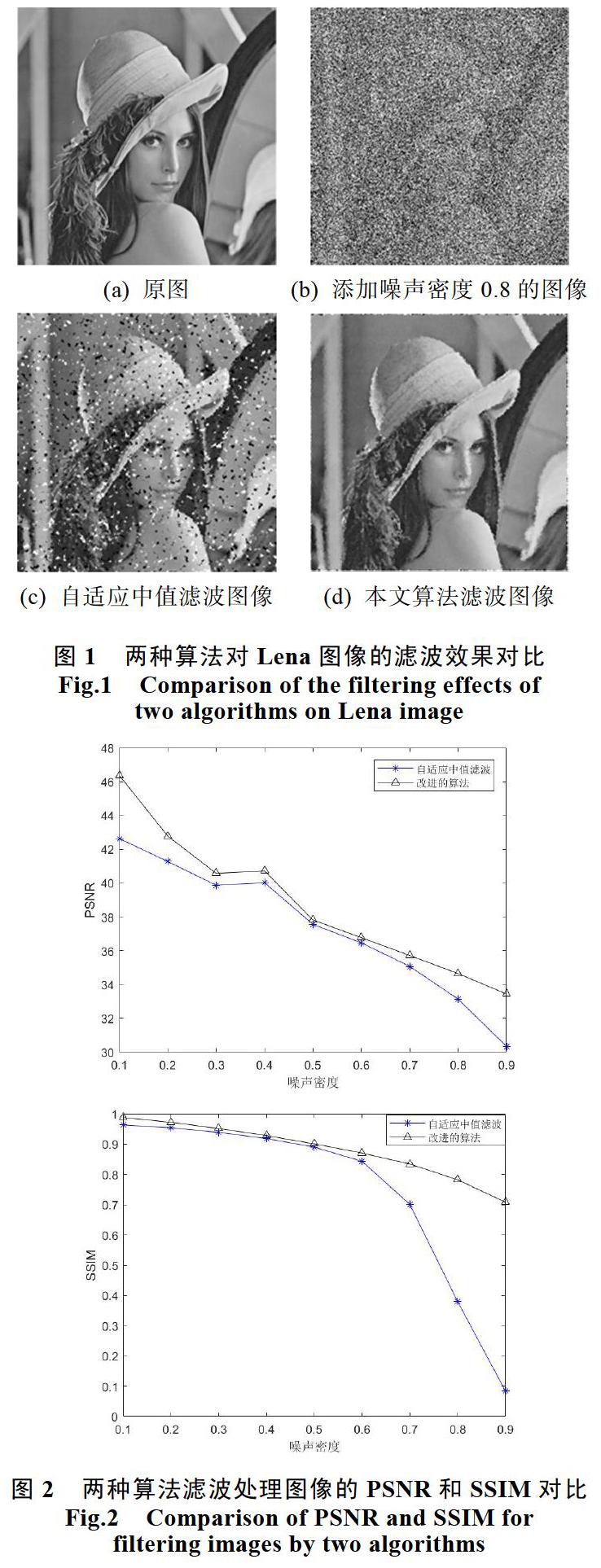
由图可以直观地看出,对于噪声密度为0.8的Lena图像,用自适应中值滤波算法滤波去噪后仍然有雪花状的噪声,而改进后的算法去噪较彻底,基本没有明显的黑白点噪声,去噪效果较好。图2为两种算法的峰值信噪比和与原图的结构相似性比较图。
由图可以看出,在各个噪声密度下,新算法的PSNR和SSIM值均比自适应中值滤波算法的高。且当噪声密度大于0.7时,新算法的PSNR和SSIM下降幅度较小,而自适应中值滤波算法的下降幅度较大,说明新算法的去噪性能更优。
4 结论
针对自适应中值滤波算法处理高密度固定值脉冲噪声去噪效果欠佳的缺陷,本文在此基础上提出了一种扩大滤波窗口时充分利用上次滤波像素值的迭代自适应中值滤波算法。对这两种算法进行了仿真实验,对比两种算法在处理相同带噪图像时的效果图,并利用PSNR和SSIM兩个参数对这两种算法进行客观的数值分析与评价。实验结果证明,新算法在提高去噪效果和保持图像细节等方面明显优于原有自适应中值滤波算法,尤其是在处理高密度固定值脉冲噪声时更为突出。
参考文献
[1]曹妍, 陈伟, 徐森. 图像去噪方法研究与仿真[J]. 软件, 2015, 36(04): 33-36.
[2]张鲁松, 张寿明. 基于ABDND算法的炉膛火焰图像脉冲噪声滤波研究[J]. 软件, 2018, 39(01): 21-28.
[3]朱志恩. 中值滤波技术在图像处理中的应用研究[D]. 东北大学, 2008.
[4]张旭明, 徐滨士, 董世运. 用于图像处理的自适应中值滤波[J]. 计算机辅助设计与图形学学报, 2005(02): 295-299.
[5]沈德海, 侯建, 鄂旭, 等. 基于改进多级中值滤波的加权滤波算法[J]. 现代电子技术, 2015, 38(12): 85-88.
[6]屈正庚, 牛少清. 一种改进的自适应加权中值滤波算法研究[J]. 计算机技术与发展, 2018, 28(12): 86-90.
[7]陈家益, 董梦艺, 战荫伟, 等. 中值检测的迭代中值滤波算法[J]. 现代电子技术, 2020, 43(07): 70- 73+77.
[8]赵玲玲. 基于自适应中值滤波算法的研究与改进[J]. 现代计算机(专业版), 2019(08): 58-62.
[9]周华. 基于动态窗口的自适应中值滤波算法[J]. 计算机应用与软件, 2011, 28(07): 141-143+166.
[10]赵新坤. 基于节点遍历法的WirelessHART快速组网设计[J]. 软件, 2019, 40(06): 208-211.
[11]丰明坤, 赵生妹, 邢超. 一种基于视觉特性的PSNR图像评价方法[J]. 南京邮电大学学报(自然科学版), 2015, 35(04): 33-38.
[12]王亮, 万舟. 基于暗原色先验图像去雾算法的研究与改进[J]. 软件, 2017, 38(09): 57-62.
[13]Tang Yiming, Ren Fuji, Pedrycz Witold. Fuzzy C-Means clustering through SSIM and patch for image segmentation[J]. Elsevier, 2020, 87(C).
[14]陈永彬, 别志松. 两种协方差估计方法的性能比较[J]. 软件, 2016, 37(11): 93-96.
