诊断高血糖高渗状态的数学模型及其应用
2020-11-30罗振国李石生
罗振国 李 星* 黄 琼 李石生 黄 丽
(衡阳师范学院南岳学院,湖南 衡阳421008)
1 概述
糖尿病高血糖高渗综合征是糖尿病严重急性并发症表现之一,病情严重的患者经常会出现严重高血糖和血浆高渗透压,不同程度神经系统障碍或昏迷,死亡率高达40% 以上。高血糖高渗状态的病人多为非胰岛素依赖糖尿病,血浆胰岛素水平比糖尿病酮症酸中毒者要高,本身有拮抗酮体作用,目前这一类糖尿病在临床上还没有有效的治愈手段,治疗的作用是在与控制血糖并延缓并发症的发作。
近年来,我国许多学者深入探讨了成纤维细胞生长因子在调控机体、维护血糖平衡、增加胰岛素敏感性等方面扮演的角色,从而证实成纤维细胞生长因子参与了调控和维持机体的血糖代谢平衡[1-3]。2016 年,文献[4]研究I 型糖尿病患者血糖控制系统,找到控制输入和控制目标输出之间的关系,得出正常血糖浓度所对应的精确控制输入,保证血糖的平衡。目前还有学者探讨了糖尿病酮症酸中毒和高血糖高渗状态,但只是研究病理生理、诱因、治疗原理等方面,没有应用数学模型来研究血糖、胰岛素、胰岛素拮抗激素之间的关系。
因此建立一个描述血糖- 胰岛素调节系统的数学模型对于量化血糖与胰岛素之间的作用,预测病人体内血糖的变化十分必要。
1.1 病理生理
高血糖高渗状态发病机制复杂,主要是肝脏与脂肪组织中的胰岛素不足,而胰岛素对抗性调节激素,特别是胰高血糖素素的升高而造成的。胰高血糖素促进了糖原分解和糖异生,皮质醇刺激蛋白质的分解,产生的氨基酸又成为糖异生的底物,从而进一步阻碍胰岛素的外周作用,加重高血糖。由于在脂肪组织中,胰岛素缺乏还有对抗激素的升高,使得激素敏感性脂肪酶活化,储存的甘油三酯被分解为游离脂肪酸和甘油,肝脏在代谢游离脂肪酸时可以不氧化出酮体,并且高渗和脱水本身也会抑制脂肪的分解,使得游离脂肪酸不会过多的进入肝脏,这也是高血糖高渗状态与糖尿病酮症酸中毒的机制的不同之处。
1.2 国内研究情况
2007 年,针对2 型糖尿病的防治,国内临床采用世界卫生组织1999 年和2003 年的标准,关于糖尿病的治疗方法,国内已经提出了药物疗法、饮食疗法和运动疗法三种方法,2013 年,有专家在中医的基础上,建立了糖尿病中医“三早”综合防治体系,但是对1 型糖尿病的诊断标准的研究相对较少。
目前国内的研究严谨性不高,研究方法单一,糖尿病性质研究主题多聚焦于糖尿病人的自我管理,心态状态,健康教育及需求等方面。但依然存在着研究对象不均衡,研究主题狭窄及角度单一的问题。
1.3 国外研究情况
2011 年,美国糖尿病学会对妊娠期糖尿病的诊断提出了新标准:对于尚未知晓是否患有糖尿病的孕妇,在妊娠24~28 周采用75g 葡萄糖耐量试验。近年来,美国科学家们在小鼠和大鼠实验中阻止了2 型糖尿病形成,取得了有一定的进展。此外,雾化胰岛素吸入治疗糖尿病在国外研究也有一定的进展。
2 模型的建立
2.1 模型假设
(1)鉴于葡萄糖是细胞组织的主要能量来源,但都有最佳的血糖浓度,假设当超过这个浓度时,将导致生病、甚至死亡。
(2)认为生理激素和其它新陈代谢是血糖含量自我调节的主要因素。
(3)假设葡萄糖只有在胰岛素的作用下才能进行大量的生化反应,从而降低血糖浓度。
(4)定义G 为血糖浓度,H 为内分泌激素浓度。
鉴于上述假设,血糖浓度的变化依赖于体内原有血糖浓度和内分泌激素浓度,把这种函数关系定义为F1(G,H),血糖浓度还与外加葡萄糖有关,记为J(t),又因为内分泌激素浓度的变化则依赖于体内血糖浓度和内分泌激素浓度,这种函数关系定义为F2(G,H)。
2.2 数据假设
(1)当没有外界摄入时,人体内有一个血糖浓度和内分泌激素浓度的平衡状态分别是G0、H0。
(2)仅仅考虑血糖浓度G 和以胰岛素为代表的内分泌激素浓度H 的相互作用。
(3)只考虑在平衡状态G0、H0附近的小偏差。
2.3 模型建立
设G(t)、H(t)分别表示t 时刻血糖与激素的浓度,则有可得增加率的平衡:
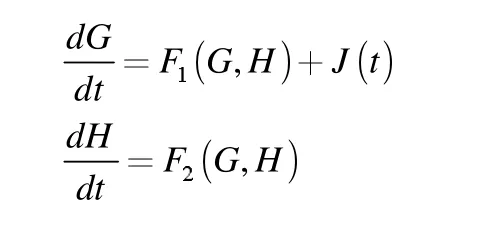
其中F1(G,H),F2(G,H)分别表示血糖浓度的变化和激素浓度的变化与G,H 的函数关系式,J(t)为t 时葡萄糖的外界摄入量。
存在G0,H0,有F1(G0,H0)=0 和F2(G0,H0)=0。令g(t)=G(t)=G(t)-G0,h(t)=H(t)-H0,则g(t),h(t)充分小,且有

将F1,F2在(G0,H0)附近展开并略去高阶无穷小,带人上式整理可得
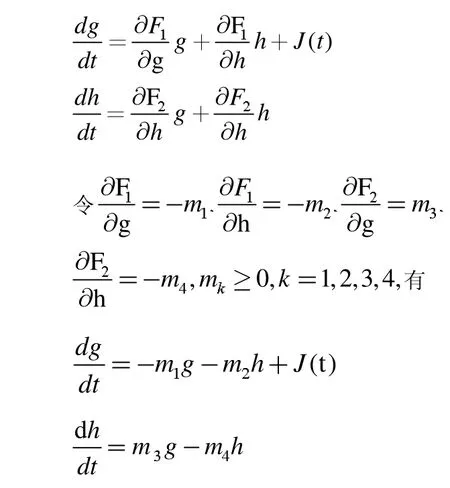
取t=0 为外部输入的G 完全被吸收的时刻,则有J(t)≡0,t>0 且g(0)=J(0)消去方程组中的变量h(t),可以得到

最后有G(t)=G0+Ae-αtcos(ωt-δ)是一条G0为平衡态的阻尼振荡曲线,与血糖曲线形状相近,其中参数G0,A,α,ω0,δ的最佳值可根据最小二乘原则,通过回归分析的方法确定。由于测量G 时的微小误差可能使α 值产生很大的误差,而参数ω0- 系统的自然频率,对于测量G 时的实验误差不太敏感,故可把ω0的值作为解释葡萄糖耐量试验的基本准则。
2.4 模型分析
(1)直接观测得到G0的值。
(2)可以取四个不同时刻(如ti=0.5,1,2,3)的血糖观测值,并求解非线性方程组得到四个参数A,α,ω0,δ 的值。
2.5 诊断指标
3 模型的应用
糖尿病作为代谢性内分泌系统疾病,可导致人体蛋白质、糖、脂肪、水等处于异常状态。高血糖高渗状态作为一种严重的糖尿病急性并发症之一,其临床特征:严重的高血糖、脱水、酮症酸中毒,导致患者意识障碍、甚至昏迷。运用上述模型可以用来求解血糖浓度与最佳浓度的偏差,诊断人体是否患有高血糖高渗状态。因此,建立的数学模型与应用的方法,对进一步调节血糖、诊断高血糖渗透状态具有一定的参考价值。
4 结论
通过建立的数学模型,将建立的微分模型运用到实际问题中去,把实际问题通过数学公式展示出来,经过科学分析处理得到定量的结果,为实际医学问题提供了理论依据,从而可以避免由于主观因素造成的误诊误治,进一步提高临床诊断和医学研究的准确性。本项目还充分的考虑了多种因素对血糖浓度的影响,更加说明了该数学模型是合理的,为临床诊断提供一定的参考价值。
