磁流变阻尼器参数化模型的研究综述

2020-11-30陶柯免

山西建筑 2020年23期

陶柯免

(同济大学土木工程学院，上海 200092)

1 概述

磁流变阻尼器(magnetorheological damper，MRD)因其结构简单、动态范围宽、响应速度快、阻尼力大且连续顺逆可调等优点[1,2]，在结构振动控制中有广泛的应用前景。为了充分发挥磁流变阻尼器良好的性能，必须建立精确且简单实用的力学模型，以保证控制算法的实时有效，从而达到对结构的精准控制。由于磁流变液的黏性特征以及外加磁场等导致MRD的非线性滞回特性，增加了建立力学模型的难度，国内外学者做了大量工作，提出了多种MRD模型，主要分为参数化和非参数化模型[3]。

参数化模型大多基于磁流变阻尼器的动力性能测试试验，从试验中可以得到磁流变阻尼器的阻尼力—位移曲线和阻尼力—速度曲线，通过预设理论表达式，进行曲线拟合，然后不断调整参数，最终确定阻尼器出力的数学表达式。比较常见的磁流变阻尼器参数化模型有Bingham模型[4]、非线性双粘性滞回模型[5]、Bouc-Wen模型[6]等；非参数化模型基于磁流变阻尼器动力性能测试试验数据，采用神经网络等智能算法来建模。本文分析了几种主要的参数化模型以及其改进型的优缺点，并对发展方向进行了阐述。

2 MRD参数化模型及其改进型

2.1 Bingham模型及其改进型

2.1.1Bingham黏塑性模型

Stanway等[7]基于电流变体的Bingham伪静力模型，提出了理想化的MRD模型，随后，Spencer等将该模型引入到MRD的动力学模型中。其力学模型由一个黏滞阻尼元件和一个库仑摩擦元件并联组成，该模型假定磁流变液屈服前为刚体且不流动，屈服后才开始流动且为非零屈服力的牛顿流体。其阻尼力的表达式为:

(1)

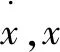
Bingham模型简单，能较准确地反映阻尼力—位移关系，但对低速区的阻尼力—速度关系却误差较大。这是因为该模型忽略了磁流变液黏弹体的本构关系。

2.1.2Bingham模型的改进型

Bingham模型虽然不能很好地描述MRD的阻尼力—速度的滞回关系，但因结构简单、概念明确，在研究初期还是得到了一些推广。

周强等[8]根据阻尼特性试验结果，将Bingham单元与一个弹性元件串联，提出了修正的Bingham模型，能较好地模拟阻尼力—位移关系，但是黏塑性单元的位移难以确定，应用较少；Occhiuzzi等[9]提出黏滞阻尼和控制电流成线性关系，将式(1)中的速度项重新描述，提出了扩展的Bingham模型，结果可以较好地描述阻尼力—速度曲线的非线性特性，但是仍然不能拟合阻尼力—速度曲线的滞回特性。

2.2 非线性滞回双黏性模型及其改进型

2.2.1非线性滞回双黏性模型

滞回特性是MRD的一个很重要的特征。由于Bingham模型及其改进型均不能体现滞回特性，Wereley等[5]在非线性双黏性模型[10]的基础上，提出了非线性滞回双黏性模型。不同于Bingham模型基于磁流变液屈服前为刚性的假定，该模型假设磁流变液屈服前后都是塑性，用6个分段函数来表示阻尼力，其表达式为：

(2)

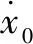
该模型基本能描述阻尼力—位移和阻尼力—速度曲线的非线性特征，使用分段函数能一定程度上反映MRD的滞回特性，但是引入的减速、加速屈服速度值随控制电流、激励的变化而变化，且得不到解决，难以应用到控制领域。

2.2.2非线性滞回双黏性模型改进型

为了改进非线性滞回线性模型的滞回曲线光滑性问题，薛建海等[11]基于式(2)，将分段阻尼力曲线简化为直线和正弦曲线组成的四段非线性函数曲线，提出了非线性滞回反正切模型，提高了MRD滞回曲线的光滑度，但是模型的复杂度和参数的确定问题并没有得到解决。

2.3 Bouc-Wen模型及其改进型

2.3.1Bouc-Wen模型

非线性滞回双黏性模型分段不连续，难以描述阻尼力—速度关系，Bouc提出了一种光滑的迟滞模型，此后Wen加以发展和完善，提出了Bouc-Wen模型[6]，其表达式为：

(3)

(4)

其中，α由控制系统和磁流变液决定；z为滞变位移；c0为MRD运动速度较大时的黏滞阻尼系数；k0为刚度系数，MRD阻尼力—速度的光滑性决定γ,β和A，以上均为常数。

该模型较Bingham模型能更准确地反映MRD低速时的非线性能力，且计算方便、通用性好，已在滞回系统建模中得到广泛应用。

2.3.2Bouc-Wen模型及其改进型

Yi等[12]针对剪切式MRD，在Bouc-Wen模型的基础上提出了修正的Bouc-Wen模型，该模型去除了Bouc-Wen模型中的线性弹簧部分，且用Bouc-Wen滞回力模拟大应变时磁流变液的库仑特性和低应变下粘弹性所表现出的复杂非线性特征。该模型简单，但是用线性关系描述电流的非线性控制影响模型精度。Spencer等[13]提出了基于Bouc-Wen模型的现象学模型，能很好地描述MRD的动态响应，且能与各速度区的实验数据相吻合，灵活性好。但是由于具有10多个待定参数，数据处理困难，在应用优化算法确定参数时容易发散。Bai等[14]引入归一化概念对现象学模型进行了简化，提出了变换现象学模型，有效地减少了模型参数的数量，简化了模型，更精确地描述MRD的非线性滞回性能。

2.4 其他模型

除上述模型以外，很多学者也提出了其他参数化动力学模型。周强和瞿伟廉[8]根据磁流变阻尼器力学性能试验结果，提出了修正的Dahl模型。该模型釆用Dahl模型模拟库仑摩擦力，相对于Bouc-Wen模型，减少了待辨识参数的个数。徐赵东等[15]提出了带质量元素的温度唯象模型，该模型能模拟阻尼器的非线性滞回性能，同时能反映温升效应对磁流变阻尼器的影响，但该模型需要解微分方程，计算速度慢。李秀领等[16]提出的双Sigmoid模型能较准确地描述磁流变阻尼器的非线性滞回性能，但不能反映位移、频率对磁流变阻尼器的影响。Chae[17]提出了Maxwell非线性滑移模型(MNS)，将磁流变阻尼器的动力学行为分成屈服前和屈服后两部分进行单独分析，并运用粒子群算法进行了模型参数识别，该模型参数少，物理意义明确，鲁棒性好，能够比较精确地描述磁流变阻尼器的动力学行为，而且在运用到实际结构控制中也能达到预期的控制效果。张香成等[18]通过对磁流变阻尼器进行力学性能试验，并基于米氏方程提出一个综合考虑电流、位移和频率影响的米氏模型，该模型能较好地模拟阻尼力—位移曲线和阻尼力—速度曲线，而且能较好地描述阻尼力—速度曲线低速时的非线性滞回性能，并能反映位移、频率对阻尼力—速度曲线滞回区域的宽度的影响。

3 MRD力学模型研究中存在的问题

由于目前对于磁流变液的微观机理认识不足，前述国内外学者对MRD进行力学建模多数仅考虑阻尼器本身参数以及磁流变液种类、结构尺寸、荷载和环境等因素。这使得通过某种型号的MRD在一定工况下进行有限次实验结果进行参数拟合得到的参数化模型，均存在各自缺陷，且鲁棒性均不甚理想。如：Bingham模型及其改进型虽然简单，但是难以描述阻尼力—速度关系；非线性滞回双粘滞模型不光滑；Bouc-Wen模型及其改进型虽然能够较准确地模拟阻尼力的动力特性，但待定系数过多，求解过程过于复杂。

鉴于参数化模型的诸多缺点，近年来以神经网络为代表的非参数化模型发展迅猛。Chang等[19]采用神经网络来模拟磁流变阻尼器的非线性动力特性，分别建立了所研究阻尼器的正向和逆向动力学模型，可用于工程结构的在线控制。廖英英等[20]采用遗传算法和BP神经网络结合，建立了MRD的逆向模型并应用于1/4车半主动悬挂系统，数值仿真结果证明其建立的模型可以较好地预测控制电流。周勇等[21]提出了一种网络连接权值自适应调整的改进RBF神经网络，有效地降低了模型的误差，能满足工程需要。相比于参数化模型，这些非参数化模型具有更好的泛化能力与鲁棒性。