改进蚁群和鸽群算法的机器人路径规划

刘 昂，蒋 近，徐克锋

（1.湘潭大学自动化与电子信息学院，湖南湘潭 411105；2.智能计算与信息处理教育部重点实验室（湘潭大学），湖南湘潭 411105）

（∗通信作者电子邮箱liuang96@163.com）

0 引言

移动机器人路径规划问题是机器人研究领域的热点，要求机器人在从起始点到目标点的运动过程中避免发生碰撞［1-2］。根据周围环境信息是否已知，将移动机器人的路径规划分为全局路径规划和局部路径规划［3-4］。现有的路径规划问题主要研究的是全局路径规划［5］，而当移动机器人运动过程中发现突发威胁时，规划出局部路径并减小路径长度和评价函数值来提高路径性能，同样是亟须解决的问题［6-7］。

国内外学者在这方面做出了大量工作。常见的路径规划算法包括蚁群算法［8］、A*算法［9］和人工势场法［10］等。文献［11］提出一种跳点搜索的方式来改进A*算法，减少对不必要节点的搜索，提高搜索效率；文献［12］提出对A*算法的启发函数引入指数衰减的加权，降低搜索节点数，提高算法搜索效率；文献［13］提出对鸽群算法的地图算子部分引入自适应权重系数，提高鸽群算法的搜索效率；文献［14］提出通过约束函数来缩小A*算法的搜索范围，提高算法的效率；文献［15］提出采用概率选择的机制区分地图算子和地标算子，提高了算法的全局搜索能力。虽然上述算法在一定程度上解决了收敛速度慢、易陷入局部最优解等问题，但仍存在路径不平滑以及未考虑突发障碍物等问题。

蚁群算法的正反馈、并行性等优点，使得其更适用于机器人路径规划等问题。鸽群算法因其在无人机航路规划等问题中表现出优秀的寻优能力而备受研究者青睐，2014 年Goel［16］首次提到了鸽群算法，但并没有将其应用到实际问题中。

鉴于此，本文提出一种基于改进A*蚁群算法与改进鸽群算法相结合的算法。首先，利用改进的A*蚁群算法进行全局静态路径规划；其次，将全局静态路径应用到鸽群算法初始化过程，使算法获得更多初始信息，并且在全局路径的基础上，利用改进的鸽群算法进行局部动态避障，使得移动机器人能够绕过动态障碍物进行局部路径规划；最后，引入B样条曲线对规划路径进行平滑化和重规划。

1 全局规划算法

1.1 改进的A*算法

A*算法于1968 年由Hart 等［17］首次提出，是启发式路径规划算法［18］。本文使用改进的A*算法来优化蚁群算法的初始信息素，减少算法的搜索时间，如图1所示。

图1 搜索示意图Fig.1 Schematic diagram of searching

实际操作时，将两个方向上当前节点的前一个节点作为其相反方向搜索的目标节点。例如，正向搜索中当前节点s3是以反向搜索中节点e2作为目标节点搜索得来的，反向搜索中当前节点e4则是以正向搜索中节点s3作为目标节点搜索得来的。这样可以保证两个方向上搜索的目标节点同时更新。为了有效提升算法的效率，将得到的优化路径记作R，并将其初始信息素设为：

其中：k为大于1的系数；C表示其他路径上的初始信息素。

1.2 引入方向评价的启发信息

本文在改进A*算法的基础上引入方向评价的启发信息，在利用估价函数f(n)计算每个扩展节点的成本之前，构建扩展节点的方向评价函数D(n)，利用方向评价函数D(n)对扩展的节点进行筛选，保留朝向目标点搜索的节点，舍去偏离目标点搜索的节点，提高搜索速度。其中，方向评价函数为：

式中：D(n)为扩展节点N 的方向评价函数；θ 为扩展节点与其父节点构成的矢量与目标点与起始点构成的矢量之间的夹角。而在本文中，起始点和目标点的坐标已知，令(x1，y1)为目标点与起始点构成的矢量的坐标；(x2，y2)为扩展节点与其父节点构成的矢量的坐标。则两个矢量的夹角可以表示为：

而父节点N -1的坐标为(xn-1，yn-1)；扩展节点N的坐标为(xn，yn)；起始点的坐标为(xstart，ystart)；目标点的坐标为(xend，yend)。两个矢量的坐标分别为：

本文采用八邻域节点扩展，当D(n) ≥0时，则保留这些节点，将其加入OPEN 表中进行后续计算；当D(n) ＜0 时，则忽略掉这些节点，加快搜索速度。

1.3 改进的蚁群算法

传统蚁群算法通过信息素的引导来进行搜索［19］。本文在传统蚁群算法的转移概率基础上引入随机选择机制来增加解的多样性。设q0为随机选择因子，q0∈(0，1)，q1为［0，1］的常数，当q0≤q1，则在排除障碍物节点和已走节点后，随机选取当前节点周围任意一个节点作为可行节点；否则按照概率转移公式来选择可行节点。具体如下：

式中：α为信息素启发因子；β为启发信息因子；τij(t)为连接顶点i，j 的边上第t 次迭代开始时的信息素浓度；ηij(t)为启发信息；rand(allowedk)表示在允许选择的栅格集合中随机选择下一步节点。

为避免蚁群算法受到非最优路径信息素的干扰而陷入局部最优，本文对信息素更新策略引入奖惩因子，即对当前迭代后的最优路径Lb增强其信息素浓度，对当前迭代后的最差路径Lw减小其信息素浓度，并且在迭代初期更应跳出局部最优，在迭代后期应逐步减少奖惩因子的影响，故引入三角函数作为系数。改进后的更新公式如下：

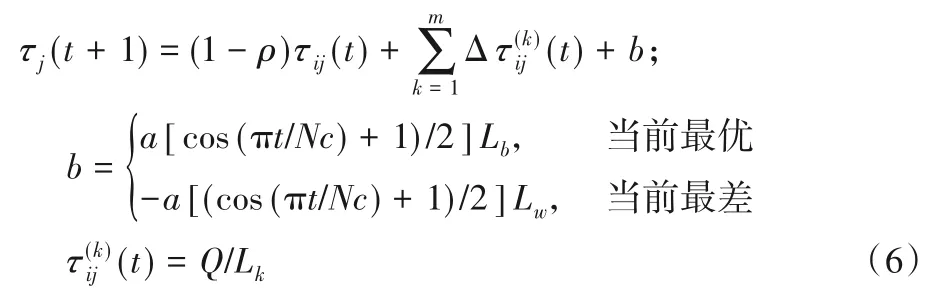
2 局部规划算法

2.1 路径评价函数

机器人路径优劣的评价函数如下所示：

式中：f 表示评价函数；f1表示威胁评价函数；f2表示路径评价函数；0 ≤k ≤1，为f1与f2之间的权重比。

f1为机器人受到的威胁评价函数，将路段分为10份，取路段上标志性的五个点来表示该段路径受到的威胁代价，则路段i受到的威胁代价［20］为：

式中：Li为路段的长度；tk为威胁因子，表示障碍物的影响程度；N 为障碍物的个数；d0.5，k为5Li/10 处的点距离第k 个障碍物的距离。

f2为移动机器人受到的路径评价函数，借鉴A*算法中的评价函数对其改进表示如下：

式中：di，i+1表示节点i 与节点i+1 之间的距离，di+1，e表示节点i+1与目标点e之间的距离。

2.2 鸽群算法的初始化

基于鸽群在归巢过程中的特殊导航行为，Duan 等［21］提出了一种仿生群体智能优化算法——鸽群优化算法。鸽群算法主要应用于无人机航路规划等领域，但是现有的鸽群算法在进行航路规划时，没有对初始路径进行初始化操作，这样导致最终的算法执行效率较低［22］。基于鸽群算法优秀的寻优能力，本文将改进的鸽群算法应用到机器人的路径规划中。静态规划阶段得出的路径可视为一个较为优秀的解集，可以将此解集作为鸽群算法的初始种群，提高算法的执行效率。

当检测到动态障碍物时，通过静态阶段设置的局部起始点和局部目标点之间的静态路径来进行鸽群算法的初始化操作。具体如图2所示。

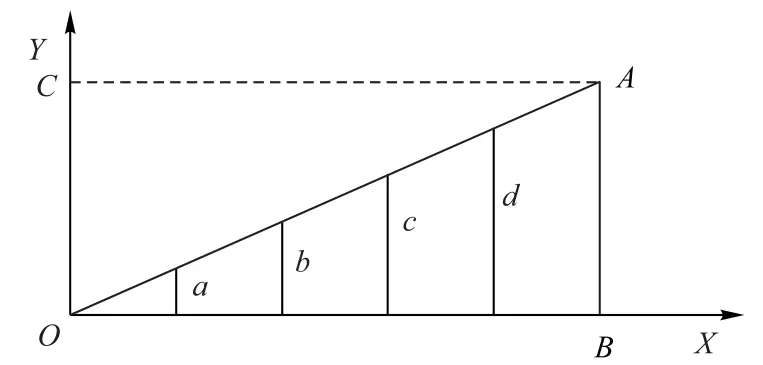
图2 初始化示意图Fig.2 Schematic diagram of initialization

在实际计算中，本文通过固定横坐标的方式来简化计算。图2 中O 点和A 点分别为局部起始点和局部目标点，将OA 沿横向作n 等分，图中的a～d 表示n -1 条等分线，路径OA 则由这样的等分线构成。本文以正态分布的形式取这些等分线上下一定数量的初始数据形成鸽群算法的初始种群。

通过上述操作，鸽群算法的初始种群由以静态路径为中心的正态分布的初始数据组成。初始种群不失随机性，同时整体质量提高，能加快寻优速度。

2.3 引入模拟退火准则的全局最优位置

鸽群算法的起始阶段使用地图算子进行搜索，每次迭代鸽子都会得到新的位置和速度。在地图算子的速度迭代公式中，e-Rt是一个递减的指数函数，在迭代后期将趋近于零，因此，地图算子十分依赖全局最优位置x'g，本文对全局最优位置进行改进，改进后的地磁算子更新公式如下所示：

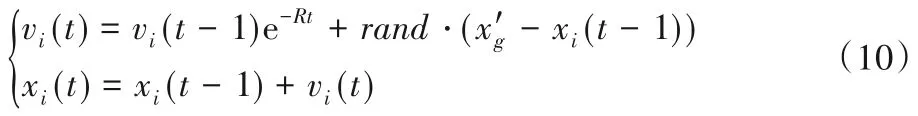
式中：vi(t)为第i 只鸽子在第t 次迭代后的速度；xi(t)为第i 只鸽子在第t次迭代后的位置；R 是地图因子；rand 是［0，1］的随机数；x'g为迭代中改进的全局最优位置。

本文对原全局最优位置引入高斯扰动，避免鸽群算法陷入局部最优，提高整个种群的多样性，具体如下：

式中：xg(t)为原全局最优位置；xG(t)为全局最优位置受到高斯扰动后的位置；r1为［0，1］的控制参数；G 是服从均值为0、方差为1的高斯分布，其概率密度函数［23］如下：

另外，在搜索过程中，应以一定的概率接受较差解，可以有效避免在迭代搜索过程中陷入局部最优，本文引入模拟退火算法来解决此问题。设扰动前的原全局最优位置xg的适应度值为f(xg)，受到高斯扰动后的全局最优位置xG的适应度值为f(xG)。如果f(xG)优于f(xg)或者下面的式（13）成立，则将受到扰动后的位置xG作为改进后的全局最优位置xg'；否则，仍使用扰动前的全局最优位置xg作为改进后的全局最优位置xg'，具体如下：

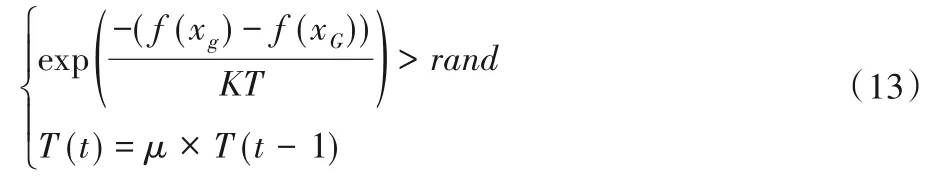
式中：K 为玻尔兹曼常数；μ 是衰减因子；T(t)为当前迭代退火温度，随着迭代进行逐渐下降。

2.4 引入自适应步长的鸽群数量

在地标算子中，迭代后期种群数量过少，影响算法寻优。地标算子阶段中，在迭代初期种群规模可以稍大一些，但随着迭代次数逐渐增大，种群规模应逐渐减小。logsig函数具有从1 到0 非线性减少的特性，故本文中引入logsig 函数作为鸽群数量的自适应步长，改进后的地标算子更新公式如下所示：

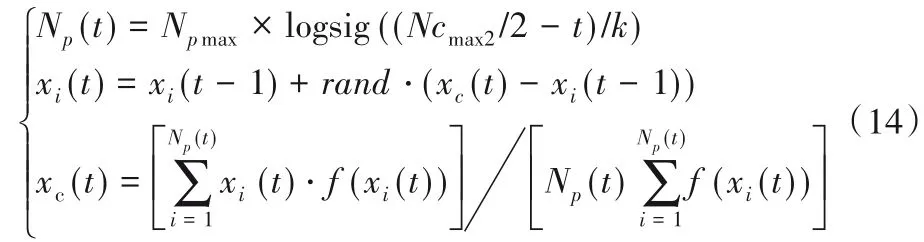
式中：Np(t)为当前迭代次数的鸽群数量；Npmax表示种群规模的数量最大值；Ncmax2为地标算子阶段的最大迭代次数；k 为logsig 函数的斜率；xc(t)代表第t 代鸽群的中心；f(xi(t))是第i只鸽子的适应度函数。改进后的种群数量呈非线性递减的变化趋势，其值逐渐减少，保证了种群多样性。

3 路径平滑化及重规划

3.1 三次B样条平滑化

实际运动过程中，要让路径尽量平滑。本文使用三次B样条曲线对路径平滑化处理［24］。B 样条曲线是Bezier 曲线的一般化形式，通过逼近多边形而获得曲线［25］。曲线平滑化的示意图如图3所示。

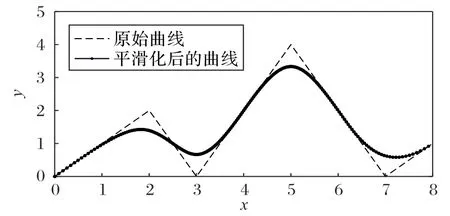
图3 平滑化示意图Fig.3 Schematic diagram of smoothing

3.2 平滑化后重规划

平滑化后若有部分路径进入障碍物内部，那么可以对该段路径中相交的碰撞部分进行重规划使路径更贴近原曲线。

具体操作为：如图4 所示，当平滑化后的路径进入障碍物内部，而原路径并未进入障碍物内部时，通过选取相交的碰撞部分的4个路径点，在4个点形成的三条边的中点取新路径点进行平滑化，并重复上述过程直至消除碰撞。

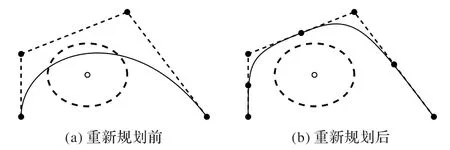
图4 重规划示意图Fig.4 Schematic diagram of replanning

4 本文算法流程

根据上述改进方案，本文整体步骤如下：

1）用栅格法建立地图模型，设置全局静态阶段的参数，包含蚁群数量m、信息素启发因子α、启发信息因子β、信息素挥发因子ρ、信息素强度系数Q、迭代次数Nc等。

2）利用改进的A*蚁群算法规划出一条静态离线路径，并对路径进行平滑化处理。

3）利用静态路径的节点，以正态分布的形式对改进的鸽群算法进行初始化，并设置局部动态避障阶段的参数，包含鸽群数量Npmax，地图和地标算子的迭代次数Ncmax1和Ncmax2，地图因子R，初始退火温度T(0)和衰减因子μ 以及logsig 函数的斜率k。

4）移动机器人通过自带传感器检测到动态障碍物时，以检测到障碍物的前一个栅格点为局部起始点，利用改进的鸽群算法进行局部动态避障，并对局部路径进行平滑化处理；否则沿原静态路径到达目标点。

5）判断移动机器人是否到达目标点，若到达，则结束整个路径规划过程；否则返回步骤4）。整体流程如图5所示。

图5 整体流程Fig.5 Overall flowchart

5 仿真与分析

从静态和动态两个方面对本文算法的性能进行仿真分析。基于栅格法并借助Matlab 2017b 平台在Windows 10 系统下进行建模仿真分析。

5.1 全局静态避障

为了验证本文算法在全局静态避障过程中的性能，在不同环境下进行仿真对比，要求路径不能与障碍物的边缘发生任何碰撞。全局静态避障阶段的蚁群数量m=20，迭代次数Nc=30，信息素启发因子α=1，启发信息因子β=12，信息素挥发因子设置为ρ=0.2，信息素强度系数Q=10。

5.1.1 环境1中仿真比较

在环境1 下对传统蚁群算法和本文算法进行对比分析，起始点坐标为（1.5，1.5），目标点坐标为（33.5，33.5）。其中，图6（a）为传统蚁群算法规划出的最优路径，图6（b）为本文算法规划出的最优路径。

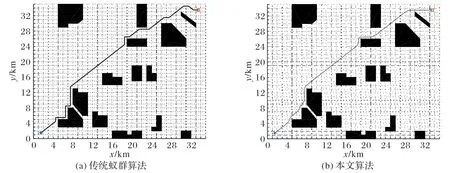
图6 静态环境1下传统蚁群算法和本文算法对比Fig.6 Comparison of traditional ant colony algorithm and the proposed algorithm under static environment 1

5.1.2 环境2中仿真比较

在环境2 下对传统蚁群算法和本文算法进行对比分析，起始点坐标为（0.5，39.5），目标点坐标为（39.5，0.5），其中，图7（a）为传统蚁群算法规划出的最优路径，图7（b）为本文算法规划出的最优路径。

5.1.3 性能指标对比

在静态环境下，对环境1和环境2下的本文算法与传统蚁群算法的性能指标对比分析。

表1给出传统蚁群算法和本文算法在两种环境下进行10次路径规划的结果。可以看出，传统蚁群算法在环境1中有3次找到了最优路径52.527 km，在环境2 中有3 次找到了最优路径71.456 km；本文算法在环境1中有10次找到了最优路径49.941 km，在环境2 中有4 次找到了最优路径66.284 km，在两种环境中的平均值分别比传统蚁群算法缩短了2.977 km和5.078 km。本文算法在环境1 下的平均执行时间2.503 s比传统蚁群算法的执行时间2.712 s，缩短了7.71%；本文算法在环境2 下的平均执行时间4.872 s 比传统蚁群算法的执行时间5.204 s缩短了6.38%。综合来看，本文算法性能更优。

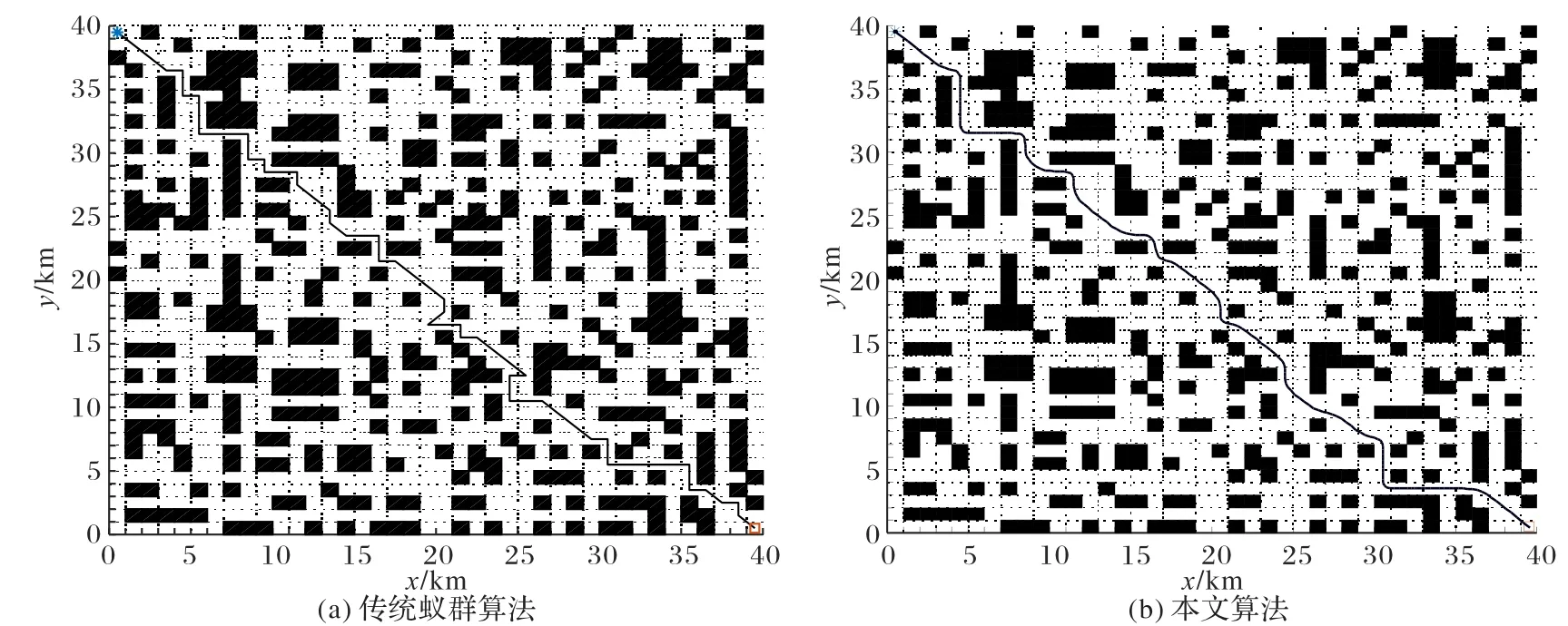
图7 静态环境2下传统蚁群算法和本文算法对比Fig.7 Comparison of traditional ant colony algorithm and the proposed algorithm under static environment 2

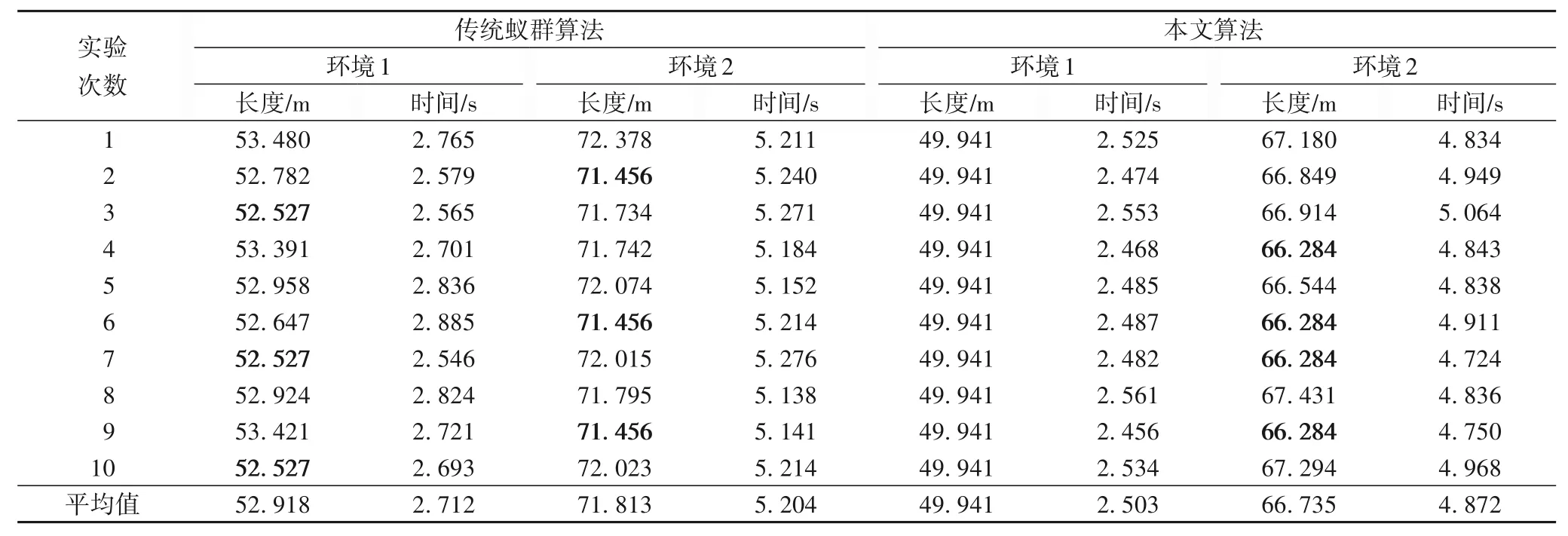
表1 传统蚁群算法和本文算法性能对比Tab.1 Performance comparison between traditional ant colony algorithm and the proposed algorithm

5.2 局部动态避障

为了验证本文算法在局部动态避障过程中的性能，在不同环境下进行仿真对比。局部动态避障阶段的鸽群数量Npmax=150，迭代次数Ncmax1=150，Ncmax2=100，初始退火温度T(0)=100，衰减因子μ=0.99，logsig函数的斜率k=5。

5.2.1 环境1中仿真比较

在环境1 中，障碍物与移动机器人的路径有部分重叠，如图8所示。图中的P点为检测到碰撞点的前一个栅格点，M点为障碍物离开移动机器人轨迹后的下一个栅格点，即此时的障碍物仅在P点和M点之间运动，P点和M点分别为局部起始点和局部目标点，其坐标分别为（9.5，15.5）和（17.5，23.5）。

图8 动态环境1下传统蚁群算法和本文算法对比Fig.8 Comparison of traditional ant colony algorithm and the proposed algorithm under dynamic environment 1

可以看出，图8（a）传统鸽群算法得出的路径性能较劣，并不能完全躲避障碍物，与障碍物的边缘仍会发生碰撞。图8（b）本文算法得出的路径与障碍物保持一定距离，且路径长度更短、更平滑化。

5.2.2 环境2中仿真比较

为了进一步验证本文算法在动态避障阶段的性能，在环境2 中，即在规划空间中随机生成大量突发动态障碍物的复杂环境下进行仿真对比，如图9所示。图中的S点表示规划起始点，E 点表示规划目标点，圆形区域表示膨胀化后的动态障碍物。从图9 可以看出，传统鸽群算法在面临数量众多突发障碍物时不能完全避障，本文算法得出的路径具有更短的路径长度且更平滑，能实现完全避障。

图9 动态环境2下传统蚁群算法和本文算法对比Fig.9 Comparison of traditional ant colony algorithm and the proposed algorithm under dynamic environment 2

5.2.3 性能指标对比

在动态环境下，对环境1和环境2下本文算法与传统鸽群算法的性能指标对比分析。表2 是传统鸽群算法和本文算法在环境1 和环境2 中进行10 次实验的性能指标对比表。可以看出，在环境1 下，本文算法在10 次实验的平均路径长度51.273 km 比传统鸽群算法平均路径长度51.406 km 要短0.133 km，并且本文算法评价函数的平均值2.621 比传统鸽群算法评价函数的平均值2.792 减小了0.171。在环境2 的复杂环境下，本文算法在10 次实验的平均路径长度62.566 km 比传统鸽群算法的70.006 km 缩短了10.62%，并且本文算法评价函数的平均值72.734 比传统鸽群算法评价函数的平均值89.841减小了19.04%。

表2 传统鸽群算法和本文算法性能对比Tab.2 Performance comparison between traditional pigeon inspired optimization algorithm and the proposed algorithm

综合上述结果来看，在相同的环境下，本文算法能规划出路径长度更短、评价函数值更小、性能更优的路径，具有更强的寻优能力。

6 结语

传统蚁群算法收敛速度较慢、易陷入局部最优解，应用到机器人路径规划时不易寻得全局最优解。本文对传统蚁群算法引入改进的双向A*算法，并对蚁群算法的转移概率和信息素更新机制进行改进。与传统蚁群算法相比，本文的全局静态路径算法可以得出更为优秀的静态路径；并且针对运动过程中出现动态障碍物的情况，本文提出一种改进的鸽群算法来实现局部动态避障。通过对传统鸽群算法的地图和地标算子进行改进，与传统鸽群算法相比，本文改进后的局部动态避障算法能更好地实现避障。最后，本文对整体路径引入三次B样条曲线进行路径平滑化处理，使路径更符合实际。

改进后的算法仍存在一些不足之处，如没有将算法放到实际场景中进行实验比较，没有在三维环境下对算法进行推广，今后将尝试研究将本文方法应用到实际场景以及三维环境下的机器人路径规划问题中。