不同缺陷下钢圆柱拱壳的稳定极限承载力

周呈祥

【摘要】本文以某钢圆柱壳屋盖为研究背景，对钢圆柱壳屋盖结构建立ansys有限元模型进行分析，通过使用大型通用有限元分析软件ansys，建立钢圆柱壳屋盖结构的有限元模型，分析探讨了不同的初始几何缺陷值对于钢圆柱壳屋盖结构稳定极限承载力的影响，并从理论层面探讨了钢圆柱壳屋盖的稳定极限承载力随着结构初始几何缺陷的变化规律，为设计制作人员提供参考。

【关键词】钢圆柱壳屋盖;初始几何缺陷;稳定极限承载力;变化规律

1.钢圆柱拱壳数值模型

钢圆柱拱壳两侧底端支座之间的水平跨度L取为20m，拱壳的轴线长度取为35m;圆柱拱壳的半径为20m，圆心角为60°，拱壳的厚度取为100mm，单元类型选用shell181壳类单元，左右两侧底边采用固定铰支座，即约束其三向线位移[1]。拱壳上部顶面承受均匀外荷载1KN/m2（即外部压强为1Kpa）。材料选用Q235钢材，弹性模量E为206Gpa，屈服强度为235Mpa，泊松比为0.3，切变模量为80Gpa。钢材的密度为7850kg/m3，重力加速度取9.8N/kg。选用理想弹塑性材料模型对钢圆柱拱壳进行弹塑性稳定分析。

2.钢圆柱拱壳特征值屈曲分析

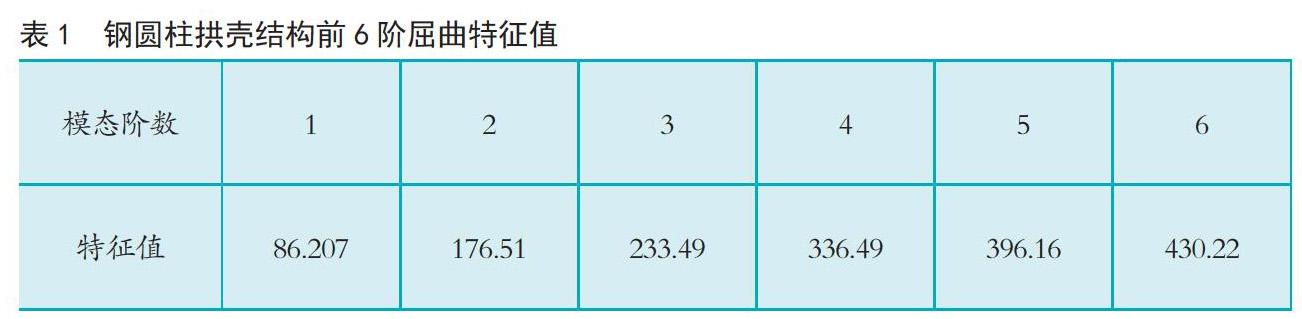
线性特征值屈曲分析可以用来初步地预测结构的理论屈曲强度，不需要进行复杂的非线性分析，就能够获得结构基于理想线弹性假定下的临界荷载及屈曲模态，并且可以为后面进行非线性屈曲分析提供参考荷载值[2]。将上文钢圆柱拱壳结构通过ansys软件分析运算并提取前6阶屈曲特征值如表1所示。

3.不同初始几何缺陷下钢圆柱拱壳的非线性稳定分析

为了考虑初始缺陷对结构理论屈曲强度的影响，必须对结构进行基于大挠度理论的非线性屈曲分析[2]。结构初始几何缺陷的施加方式可采用结构线性特征值屈曲分析时得到的最低阶屈曲模态作为初始缺陷的分布模态[3]。这是因为结构的最低阶屈曲模态是结构屈曲时的位移倾向，是潜在的变形趋势，如果结构的缺陷分布恰好与结构的最低阶屈曲模态吻合，此时势必对结构的稳定性产生最不利的影响[2]。因此本文采用一致缺陷模态法对结构进行缺陷影响分析。

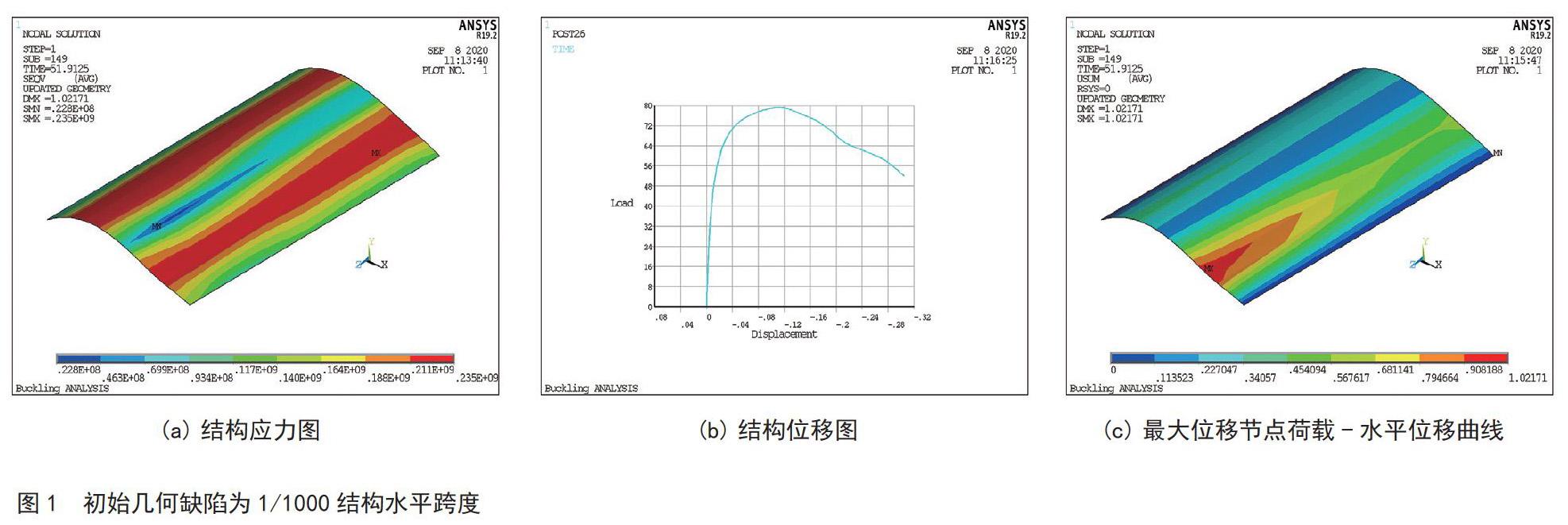
首先对初始几何缺陷为1/1000结构水平跨度的情况进行分析探讨，通过弧长法进行弹塑性全过程分析，并设置分析的终止条件为跨中拱顶节点的水平位移达到0.15m时停止运算，读取最后一个子步对应的结果，可分别得到钢圆柱拱壳结构的应力云图、位移云图以及最大位移节点的荷载位移曲线[1]。

由图1（a）结构应力云图可知，此时钢圆柱壳结构已有大片区域的应力达到屈服强度235Mpa，即结构已经进入了弹塑性工作状态;由图1（b）可见结构位移最大的地方并不在跨中拱顶节点，而是位于拱顶偏右侧的位置，其水平位移甚至达到了0.3m左右[1];由图1（c）可提取荷载位移曲线上第一个临界极值点处的荷载系数为79.17。即初始几何缺陷为1/1000结构水平跨度时，钢圆柱拱壳的稳定极限承载力为79.17KN/m2（即79.17Kpa）。

按照类似的分析方法分别对初始几何缺陷为L/5000、L/2000、L/500、L/300、L/200、L/150（L为结构两侧底端支座间水平跨度距离）的钢圆柱拱壳进行分析，可分别得到不同缺陷下结构的应力图、位移图、荷载-位移曲线图。从以上弹塑性全过程分析荷载-位移曲线图上可分别提取得到第一个极值点处的临界荷载系数，这里的临界荷载系数即为结构的稳定极限承载力。将提取的临界荷载系数汇总于表2。

观察表2，可以发现该钢圆柱拱壳对初始几何缺陷较为敏感，随着初始几何缺陷的不断增大，钢圆柱拱壳的稳定极限承载力系数单调下降。初始几何缺陷从L/5000增大到L/150的时候，承载能力从最初的84.16KN/m2到56.52 KN/m2下降了整整28.09 KN/m2。

若以L/5000初始几何缺陷算出来的结果为参考基准，可求得其余情况下承载力的下降百分比。值得注意的是，当初始几何缺陷达到L/300的时候，稳定极限承载力已经下降了20.23%;当缺陷达到L/150的时候，稳定极限承载力甚至下降了33.2%。可见初始几何缺陷的存在使得结构自身的承载能力大打折扣。

4.结论

通过上述研究分析，可以得出如下结论：

（1）线性稳定分析算出来的承載力普遍高于非线性分析算出来的结果。实际上，前者未考虑几何非线性、材料弹塑性及初始几何缺陷，是较为理想化的。而后者算出来的结果更有工程参考价值。

（2）该钢圆柱拱壳屋盖结构对缺陷比较敏感。在一定的范围内，随着初始几何缺陷值的不断增大，结构的稳定极限承载力单调下降。以初始几何缺陷为L/5000算出来的稳定极限承载力结果为基准，当初始几何缺陷值达到L/300的时候，结构的稳定极限承载力已经下降了20.23%。当初始几何缺陷值达到L/150的时候，结构的稳定极限承载力甚至下降了33.2% 。

（3）鉴于结构的初始几何缺陷会显著地降低结构的稳定极限承载力，因此在制作安装的过程中需要严格控制误差，保证精度。在设计时也应给予结构一定的安全储备。

参考文献

[1] 熊令芳.ANSYS工程结构数值分析方法与计算实例[M].北京：中国铁道出版社，2015.

[2] 韩庆华.大跨建筑结构[M].天津：天津大学出版社，2014.

[3] 赵鹏飞.空间网格结构技术规程理解与应用[M].北京：中国建筑工业出版社，2012.

（作者单位：广西大学土木建筑工程学院）

【中图分类号】TU378.3

【文献标识码】B

【文章编号】1671-3362（2020）10-0056-02