重视例题教学中的思维启迪

蔺红帅

笔者认为，在目前的课堂教学中，如何充分运用例题教学进行思维启迪并未引起广大教者的足够重视，结果是例题天天讲，有些题还反复讲，但学生水平仍难见长进，导致老师讲得愈多，学生厌学情绪愈浓。我们在教学实践中体会到，激发学生的内生动力，重视思维启迪是提高例题教学质量的重要举措。今举一例，介绍我们的做法，仅供参考。

以下我们分三个层次进行思维启迪，引导学生探究证题思路。

一、一般性启迪

给出例题后，如果教师仅仅给出一种证法，而忽略思维启迪，就会使学生误以为解题就是获取结果（答案），面对具体问题盲目下手，急于求成，结果欲速不达，甚至半途夭折。教学中，我们首先要求学生回忆常用的数学方法（如推理证明法、计算证明法），这是一种方法论水平上的启迪，它提示学生注意运用一般性的思考原则和方法总览全局，其目的是帮助学生把握解题方向，扩大思维通道，提高思维层次。

二、功能性启迪

功能性启迪是基本数学方法水平上的启发，它引导学生充分挖掘题设条件所蕴含的数量关系和图形属性，挑选其中的事实和性质来使问题获解。这里教师应恰当地提示学生思考的序列，使学生从新到旧、由近及远地展开思维活动。

在运用推理证明法时，我们提示学生遵循“欲证线线垂直，需证线面垂直”这个原则进行思考。学生就会在“证A1M垂直于过AB1的平面”或“证AB1垂直于过A1M的平面”这两种途径之中作出选择。这种选择往往带有偶然性，或许两种途径都行得通，或许只有一种途径可行，如果其中一种途径不易实现时，应迅速更换途径，从而使解题有的放矢，少走弯路。

在运用计算法证明A1M⊥AB1时，我们提示学生遵循“平移直线，构造三角形”這个原则探究证题途径，特别提醒学生利用特殊点：线段的端点或线段的中点构造三角形，这样的思维活动围绕“运用条件，解决问题”这个中心展开，促使学生全方位、多角度地审视命题，充分运用所学知识和掌握的数学方法，各显神通探究思路，从而有效地拓宽了证题的路子。

三、特殊性启迪

特殊性启迪是启发学生运用具体的解题方法和步骤。此时，应按照一般性启迪和功能性启迪中的思考原则，多角度地探究证题方法。

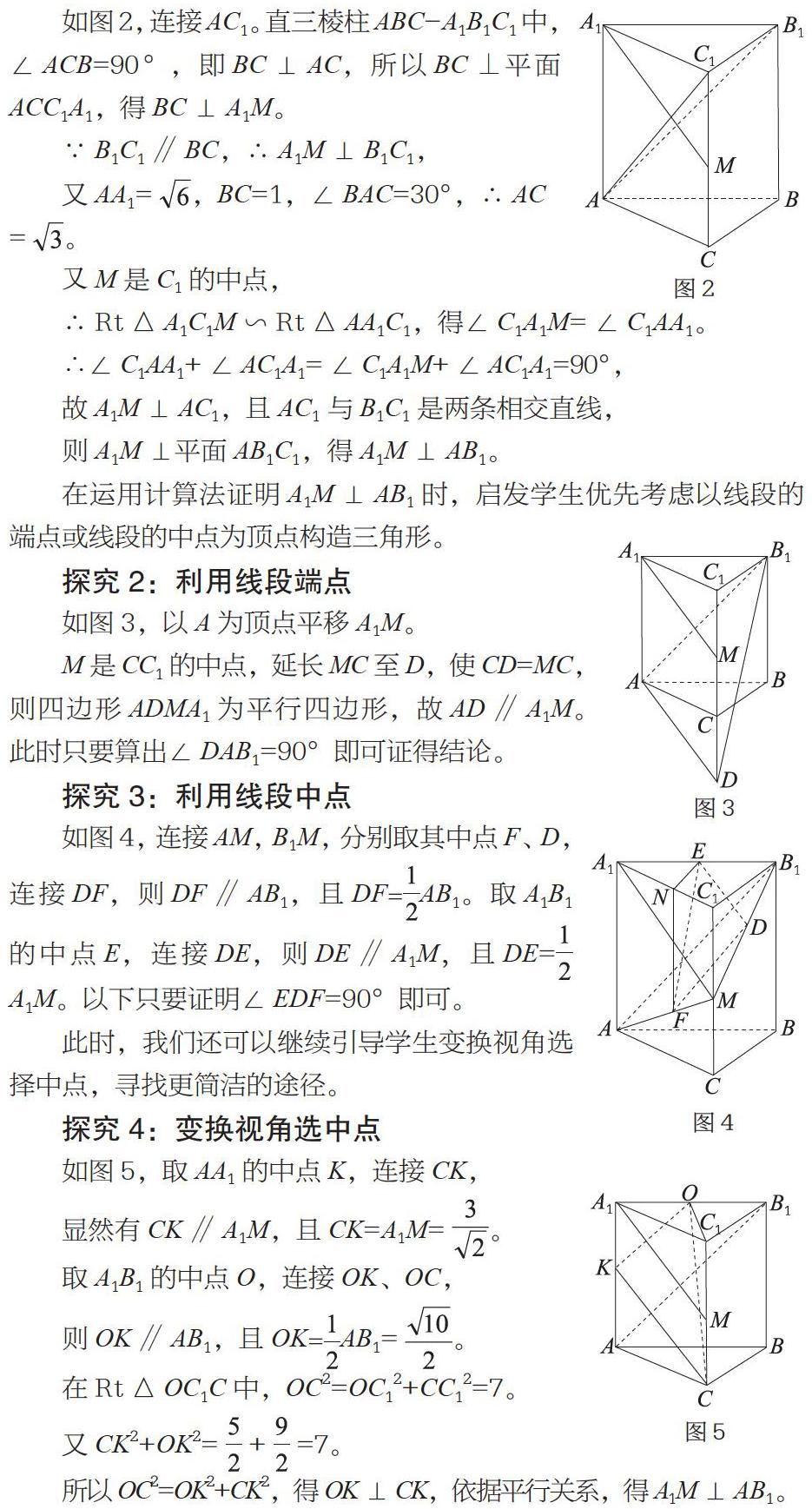
探究1：利用线面垂直

首先，引领学生借助直觉判断不易证AB1垂直于过A1M的平面，迅速调整方案，改证A1M垂直于过AB1的平面，并利用图形特征先易后难地寻找线线垂直关系。学生容易给出具体证法如下：

在运用计算法证明A1M⊥AB1时，启发学生优先考虑以线段的端点或线段的中点为顶点构造三角形。

探究2：利用线段端点

如图3，以A为顶点平移A1M。

M是CC1的中点，延长MC至D，使CD=MC，则四边形ADMA1为平行四边形，故AD∥A1M。此时只要算出∠DAB1=90°即可证得结论。

探究3：利用线段中点

如图4，连接AM，B1M，分别取其中点F、D，连接DF，则DF∥AB1，且DF=AB1。取A1B1的中点E，连接DE，则DE∥A1M，且DE=A1M。以下只要证明∠EDF=90°即可。

此时，我们还可以继续引导学生变换视角选择中点，寻找更简洁的途径。

探究4：变换视角选中点

多角度探究解题路子，就容易在比较中获取最佳途径，使解题收到事半功倍的效果。

我们在长期的教学实践中体会到，例题教学中，例题并非多多益善，而应重视思维启迪，引导学生在积极的心智活动中开阔思维通道，灵活调控思维，优化解题途径，才是切实提高学生独立分析问题、解决问题能力的有效举措。