履带起重机细长桁架臂稳定性系数探讨
2020-11-27高顺德马晨旭徐金帅
高顺德,马晨旭,徐金帅,朱 磊
(1.大连理工大学 机械工程学院,辽宁 大连116024;2.大连理工大学 运载工程与力学学部,辽宁 大连116024)
0 引言
随着科学技术的发展,起重机广泛应用于各种领域行业。在起重机臂架结构中,桁架臂因自重、迎风面积和抗弯性能等良好的特点,得到了广泛的应用。随着制造技术的提高和高强材料的引进,起重机桁架臂柔性和高耸性的特点,使得臂架越来越细长,其起重能力和工作空间也得到了较大的改善。对长细比桁架臂而言,由于几何非线性因素的影响,臂架在结构失稳后会引起较大的几何变形,造成的破坏程度远大于强度破坏。因此,臂架的非线性稳定性分析对臂架稳定性能有着不可缺少的重要影响。
目前,非线性问题的研究主要分为几何非线性。随着臂架这种桁架结构越来越细长,在施加轴向和自重载荷时,臂架的刚度会在原有的基础上减小,臂架结构进一步产生二次变形,产生较大的位移变形,这属于大位移几何非线性范畴。
几何非线性屈曲用于分析大变形或大转角结构的稳定性。通过对非线性平衡方程,得到高精度的载荷-位移曲线,可以反映结构屈曲时的状态变化。
起重机工作时受水平倾斜,臂架、吊载受风载荷及回转惯性载荷的影响,保证臂架结构在工作过程中的侧向稳定性是臂架设计过程中所面临的关键问题。根据臂架在作业系统中的受力和约束情况[1],本文分析了受几何非线性影响的臂架稳定性,并对不同工况下的稳定性系数作了对比,得出了在不同侧载情况下的稳定性系数近似值,为起升载荷的选取提供参考。
1 稳定性理论
结构稳定性是指结构在载荷的作用下保持其原有平衡状态的能力。在外界载荷的作用下,结构能够维持平衡状态,所施加的载荷增加到一定数值时,结构的应变和应力由于外界微小的扰动而不成比例的变化,内部阻力突然崩溃以致结构完全失去抵抗,从平衡稳定状态转变为到不平衡状态,结构因此失去稳定性,或称为屈曲,失稳对应的载荷又称为屈曲临界载荷或失稳载荷[2,3]。
工程中有一类结构在施加载荷后会有相对明显的变形,如履带起重机纤细的桁架臂结构,横截面积较小,严重存在刚度不足的问题,负载的重量将出现较大的初始挠度变形,在受到轴向荷载和水平荷载时,容易出现“软化”现象[4]。因此,不能忽视几何非线性效应对臂架结构应力和变形的影响。
在研究几何非线性问题时,结构会产生大位移、大转度或大应变,因此需要考虑平衡方程和几何运动方程,几何方程中还需要考虑单元大小和形状的变化。对于柔性臂结构,也存在大变形、小应变,应变虽小,但结构受力后会产生较大的位移,大变形对平衡状态影响较大。
由于臂架结构复杂,几何非线性研究中需要考虑的方程自由度的数目较多,常采用数值方法求解。由于失稳临界点附近的刚度矩阵接近奇异点,因此对于非线性稳定问题,采用弧长法来跟踪载荷-位移曲线[5]。
2 起重机臂架有限元模型
2.1 臂架简化模型
本文的研究对象是650 t 的履带起重机,选取84 m 和96 m 两种不同长度的主臂,每种臂长同时考虑12 m、14 m 和16 m 三种不同起升幅度并进行加载不同侧载的几何非线性有限元稳定性分析研究。主臂臂架由底节、标准节和顶节构成。
为了臂架结构的受力条件符合实际作业情况,保证有限元计算的正确性,建模时,臂架弦杆与腹杆均采用Beam188 梁单元,拉板采用Link180 杆单元,模型尺寸按臂架实际结构尺寸建立。为了更有效的研究臂架几何非线性产生的影响,在建模时认为变幅拉板具有良好的刚度,始终处于弹性阶段不受材料非线性的影响,拉板面积选定为5 500 mm2。臂架结构的有限元模型如图1 所示。

图1 主臂有限元模型
2.2 模型加载方式与边界条件
变幅拉板末端限制全位移约束三个自由度,在主臂根部铰点处施加ROTX、ROTY 旋转约束和UX、UY、UZ 位移约束。起升载荷施加在臂头处。表1 为不同计算工况的,加约束条件后的模型如图2 所示。

图2 主臂施加约束

表1 650 t 模型载荷工况
3 载荷-位移曲线分析
以96m 长主臂为例进行分析。图3 是该模型在主臂臂头节点观测点的载荷-位移曲线图。
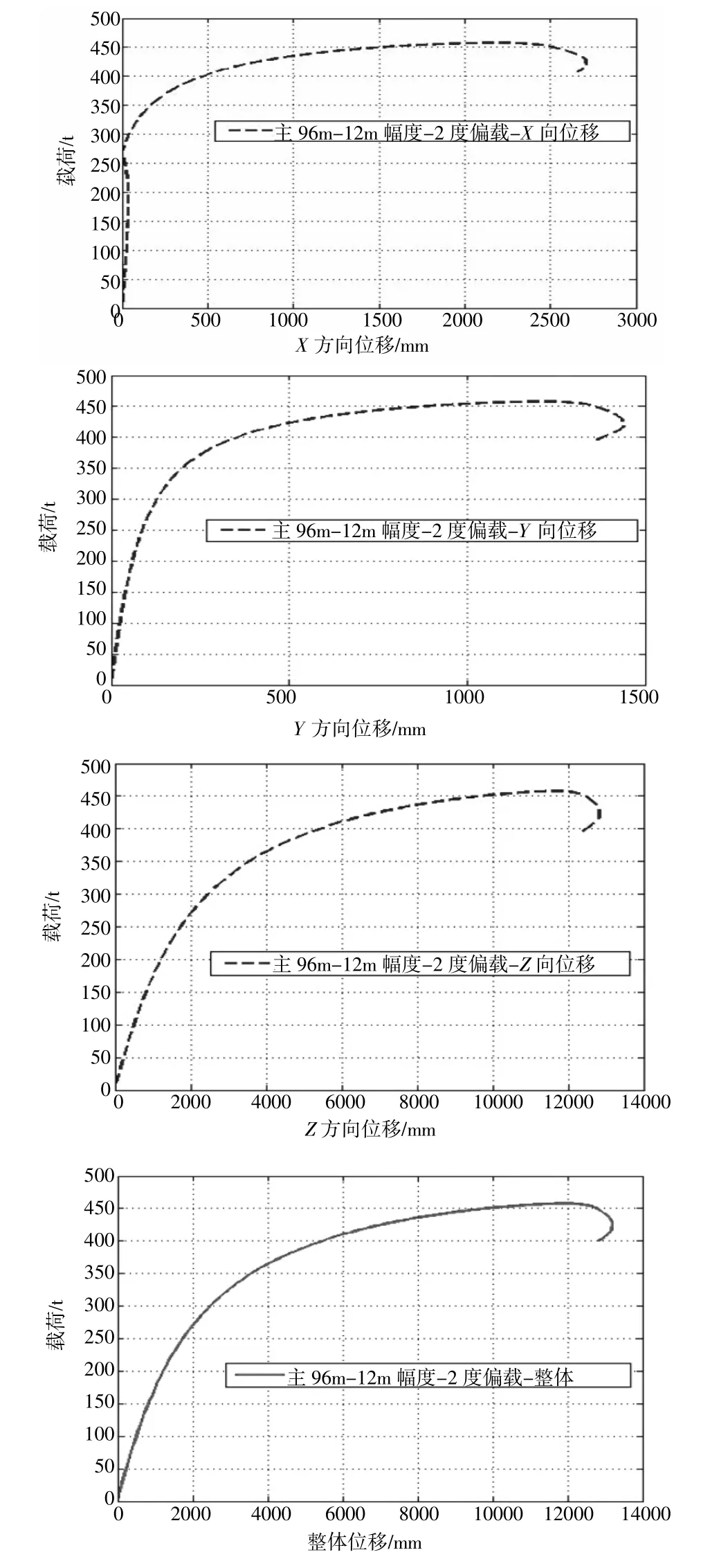
图3 主臂96 m~12 m 幅度单方向与整体方向载荷-位移曲线
单方向的载荷-位移曲线表明,X 方向的载荷-位移曲线在加载力到达300 t 之前,斜率梯度变化很小,而Y 方向和Z 方向的曲线变化趋势和X 方向的变化趋势明显不同。载荷在300 t 至到达失稳点之前,曲线斜率逐渐逐渐发生变化,呈现出减小的趋势,越过失稳载荷后,X 方向位移继续增大,直到臂架失去承载能力。Y 方向的载荷-位移在载荷达到300 t 之前,其位移与载荷基本保持线性关系,体现了线性的结果;在载荷到达300 t 后和失稳前,曲线斜率逐渐减小,结构呈非线性,臂架体现了非线性带来的影响。而Z 方向的曲线于整体载荷-位移曲线最为接近,结构非线性明显。
从载荷-位移综合曲线来看,在施加侧载的情况下,曲线起初阶段,随着位移的增大,载荷也随之增大,载荷位移曲线接近直线,结构的非线性关系不明显,体现了线性的影响。当载荷增加到250 t 左右时,曲线的斜率开始减小。载荷幅值的变化远小于位移的变化,在达到失稳极值点之前,表现出明显的非线性。在荷载达到失稳载荷之前,该阶段刚度矩阵为正,结构处于稳定状态。在极值处,结构处于临界状态,此时的载荷称为临界荷载。当曲线达到各自的极值后,结构开始失稳。
从三个载荷-单向位移曲线可以看出,Z 方向位移变化主导了综合位移的趋势。这是因为在变幅平面内,主臂头部受变幅拉板的约束作用,而回转平面内,臂架头部不受约束,施加侧载就会导致较大的侧向位移。因此在臂架失稳后,臂头侧向位移急剧增大,承载能力迅速下降,结构被完全破坏,直到失去承载能力。
4 载荷-位移结果对比分析
4.1 改变起升幅度的稳定性结果对比
图4 是主臂长度相同,施加同一侧载情况下,不同起升幅度的载荷-位移曲线对比结果,从图中可以看出,在主臂相同、侧向载荷相同的情况下,随主臂起升幅度的增大,臂架的失稳载荷增大,臂架的承载能力变强,且跃过失稳点后,臂架的承载能力下降得越加迅速,位移大小的变化越加反复与剧烈,这是因为随着幅度增加,由于拉板与吊载与臂架角度的变化,相同载荷时臂架的轴向力变小,因此其极限载荷会增加。
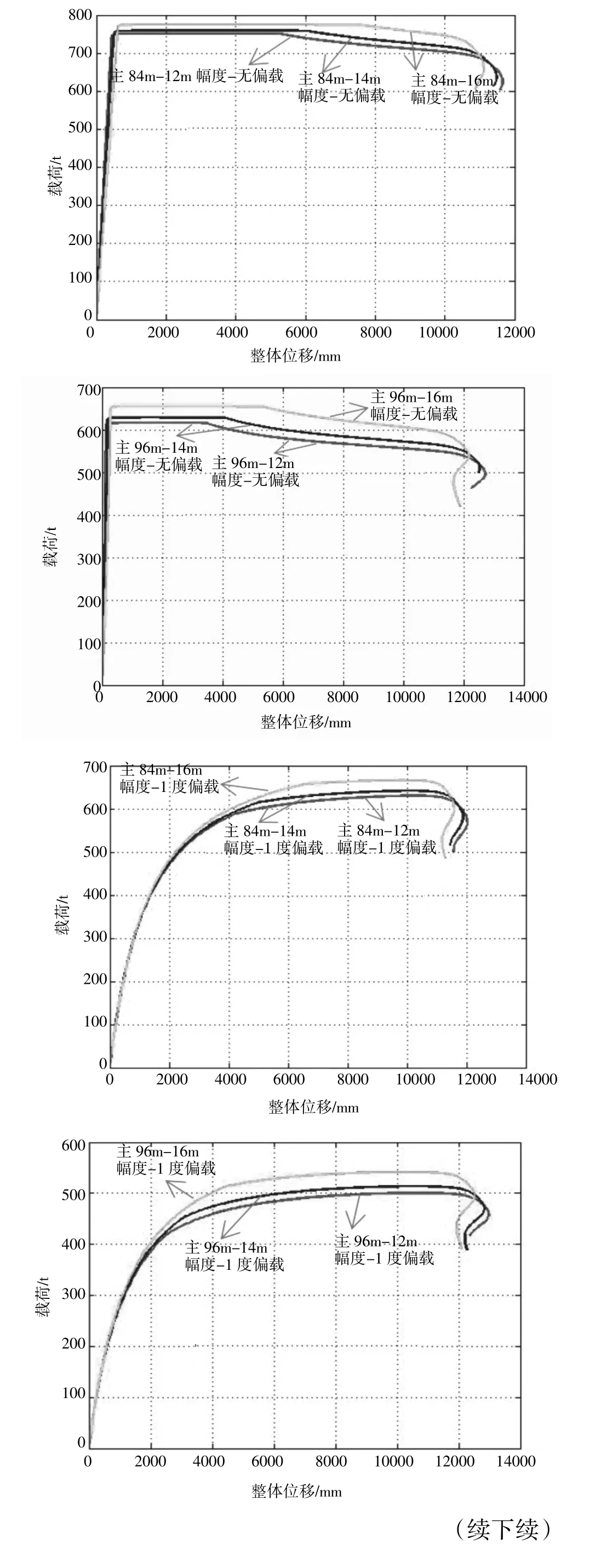
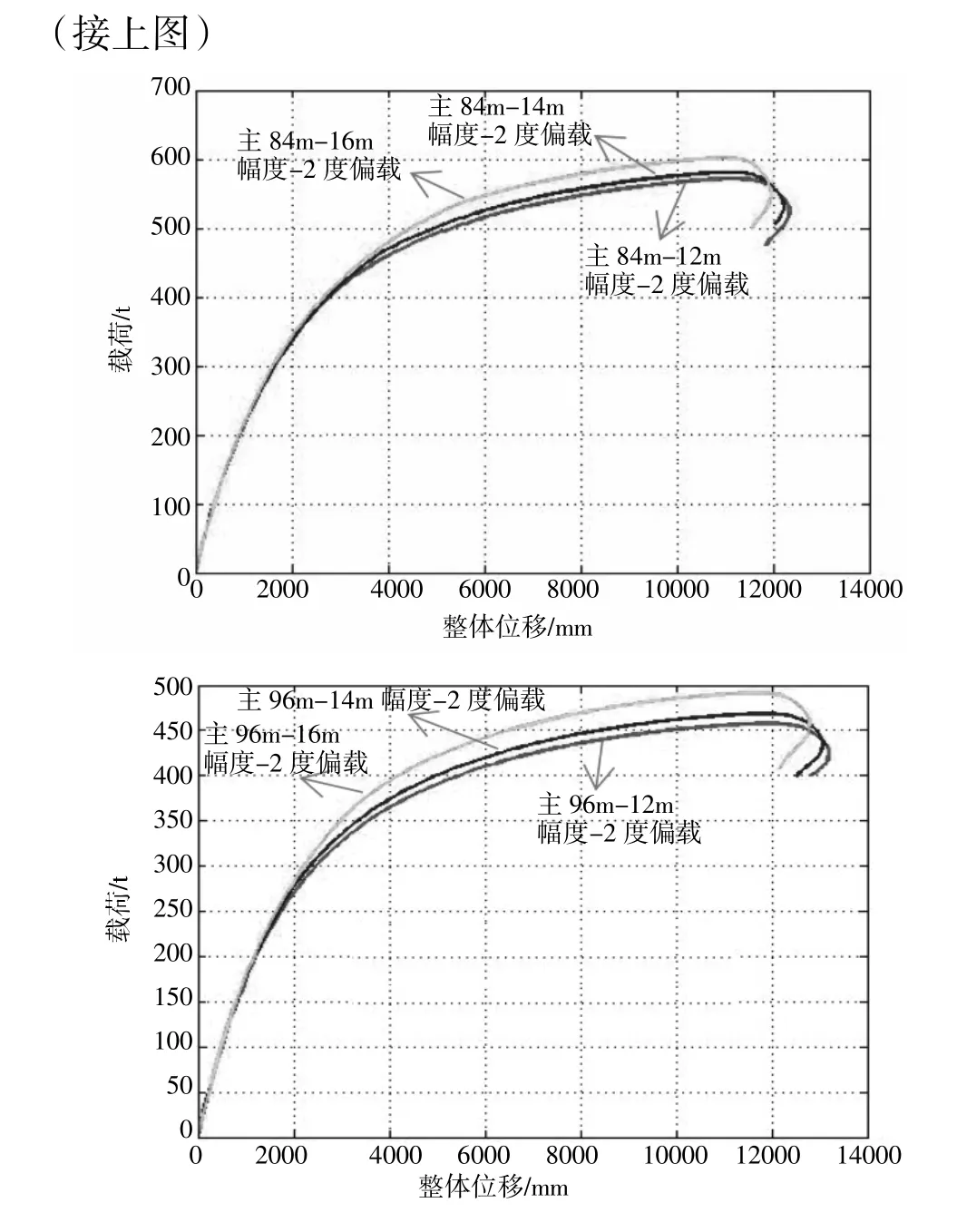
图4 相同主臂同一侧载不同起升幅度载荷-位移曲线
4.2 改变侧向载荷稳定性分析
图5 是相同臂长同一起升幅度不同侧载载荷-位移曲线对比图。在主臂长度相同、起升幅度一致的情况下,不施加侧载的时,臂架在起始阶段,曲线载荷急剧增大,此时成线性关系,到达极值点后,载荷位移曲线保持平稳,承载能力最强,之后成下降趋势,位移增加,载荷减小,承载能力降低。当施加侧向载荷时,载荷位移曲线成非线性关系缓慢增加,到极值点以后,臂架结构的承载能力迅速下降。由此可见,随着侧向载荷的增大,主臂臂架的承载能力显著下降,位移也会增大。即施加侧载相对于无侧载结构的刚度有所降低,臂架变形偏大。
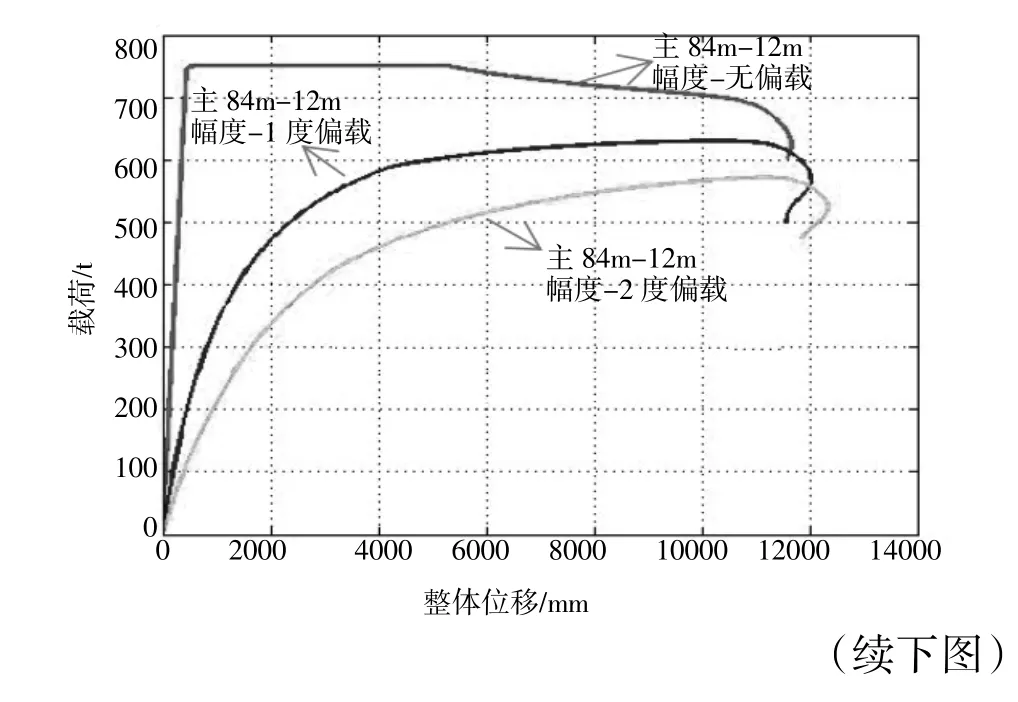
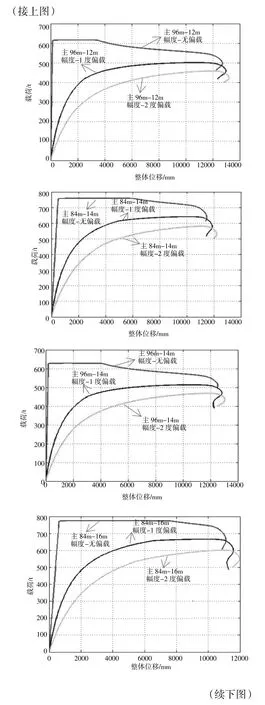
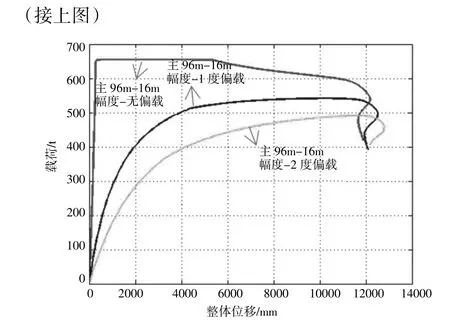
图5 相同臂长同一起升幅度不同侧载载荷-位移曲线对比
4.3 稳定性系数对比
图6 和表2 为84 m 和96 m 臂长在不同工况下稳定性系数,可以看出,在同一工况下,随着臂长的增加,稳定性系数也随之增加;在同一臂长下,随着侧向载荷的增加,稳定性系数随之减小,呈负相关关系。这是因为,大型起重机臂架是一种重载、柔性、细长结构,在重载条件下,细长的臂架结构在侧向载荷以及重载的双重作用下会产生大位移,使失稳载荷减小,稳定性系数降低。
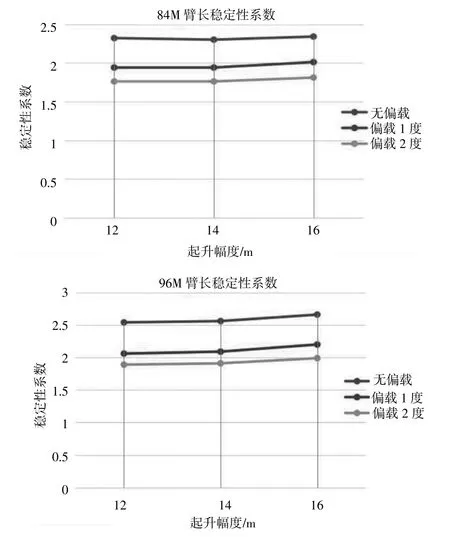
图6 84m 和96m 臂长在不同工况下稳定性系数对比结果
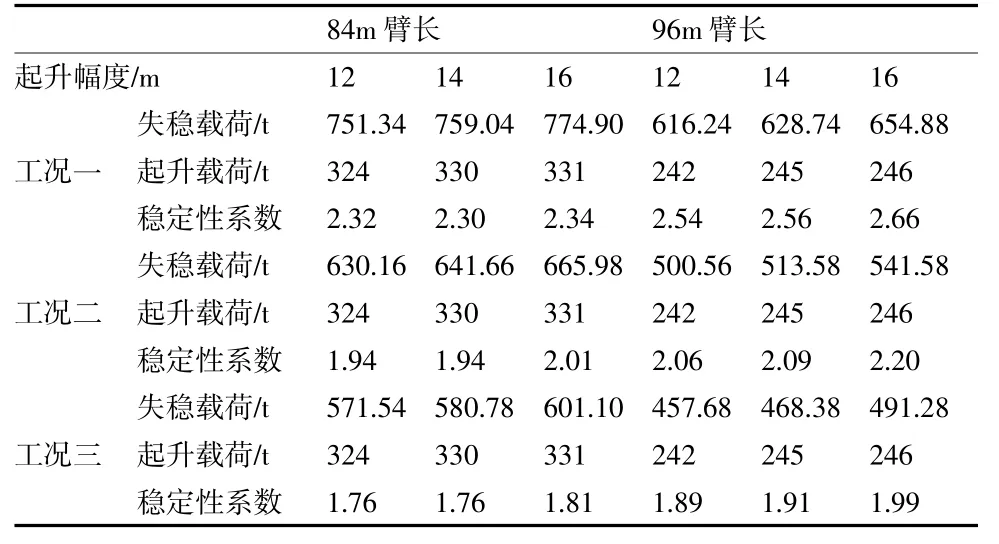
表2 84m 和96m 臂长在不同工况下稳定性系数
5 结束语
本文计算工况均为超起工况,在小幅度工况,长臂架主要是由臂架稳定性决定,因此得出以下结论:
(1)臂架在侧向载荷作用下其几何非线性效应更加明显,施加侧载,主臂会导致更大的侧向位移,更容易失稳,且失稳载荷要比不施加侧向载荷时小。
(2)在不施加侧载情况下,主臂的稳定性系数可选2.3 左右,在施加一度侧载时,稳定性系数可选2.0左右,在施加两度侧载时,稳定性系数可选1.8 左右。考虑起重机水平倾斜,臂架、吊载受风载荷及回转惯性载荷的影响,臂架为稳定性系数并不是不变的,本文的计算可为起重机起升载荷的选取提供参考。
