故障加强超立方体中的边泛圈

张艳娟,刘红美

(三峡大学理学院,湖北 宜昌 443002)

1 引言

基于VLSI技术的迅猛发展,一个多处理机系统含有大量的节点.在系统实现过程中,无论节点还是链接发生故障的可能性都是不可避免的,因此对系统作容错性能分析是非常重要的课题.当故障发生时,一个系统能保持一定的功能,则称该系统是容错的.判断一个系统是否保持一定功能的标准之一就是看系统是否含有某种拓扑结构,这种问题经常表现为把一种结构嵌入到另一种结构中.本文主要关注在节点发生故障时,系统中每条链接是否在各种长度的圈型结构中.通常用G=(V,E)来表示一个图,图的顶点集V表示网络节点集合(或称点集),图的边集E表示网络链接集合(或称边集).网络G中最小圈长,称为G的围长,用g(G)表示.若图G含有长为l的圈,其中g(G)≤l≤v(G),v(G)=|V|是G的节点数（或称阶）,则称G是泛圈的(pancyclic).网络是否具有泛圈性可以度量该网络是否可以嵌入任意长度的圈.若G中每条边均位于长从g(G)到v(G)的圈上,则称G是边泛圈的(edge-pancyclic)．若含有从g(G)到v(G)的所有偶数长度的圈(简称偶圈),称G是偶泛圈的(bipancyclic)；若对G中的每条边,均存在长度从g(G)到v(G)的所有偶圈经过该边,则称G是边偶泛圈的(edge-bipancyclic)．如果G的点集可以划分为两个非空不交子集X、Y,使得G中每条边的端点分别属于X、Y,则称G为二部图.二部图不含长度为奇数的圈（简称奇圈）.因此二部图仅研究其偶泛圈性和边偶泛圈性.以超立方体为拓扑结构的网络简称超立方体网络,它是典型的二部图,由于其结构正则,对称,具有点边传递性、相对小的传输延迟、路可嵌入性、圈可嵌入性、树能以膨胀系数1嵌入等优良性质而受到广泛关注(见文献[1–3]),在高性能计算机中,尤其在大型工业计算和研究中,超立方体结构有着非常重要的作用.n-维超立方体,记为Qn.随着可靠性容错性要求的越来越高,许多改进的超立方体拓扑结构相继提出,比如折叠超立方体FQn,加强超立方体Qn,k,可扩超立方体AQn,交叉超立方体CQn,广义超立方体等等[3].

超立方体及其变形结构的泛圈性以及容错泛圈性的研究近来得到了许多好的结果.文献[4]证明了Qn,k为二部图当且仅当n和k有相同奇偶性．因此,当n和k有相同奇偶性时,对Qn,k需要考虑偶泛圈的嵌入;当n和k有不同奇偶性时,要同时考虑奇圈和偶圈的嵌入．文献[5]证明了当|Fv|=1时,若n和k有相同奇偶性,则Qn,k中存在长度从4到2n−2的偶圈；若n和k奇偶性不同,则Qn,k中不仅存在长度从4到2n−2的偶圈,而且还存在长度从n−k+2到2n−1的所有奇圈.在此基础上,文献[6]进一步证明了当|Fv|=2,若n和k有相同奇偶性,则Qn,k中存在长度从4到2n−4的偶圈；若n和k有不同奇偶性,则在Qn,k中不仅存在长度从4到2n−4的偶圈,而且还存在长度从n−k+2到2n−3的奇圈．同时文献[6]还证明了当|Fv|≤n−2时,若n和k奇偶性相同,则Qn,k存在长度2n−2|Fv|的偶圈;若n和k奇偶性不同,则Qn,k存在长度2n−2|Fv|的偶圈,同时存在长度从2n−2|Fv|+1的奇圈.折叠超立方体是加强超立方体中k=1时的一种特殊情形,关于折叠立方体的容错性能也有很多好的结果.文献[7]证明了在折叠超立方体FQn(n≥4)中,当|Fv|=2n−3,FQn−Fv中存在一个长度至少为2n−2|Fv|的圈．文献[8]进一步推广上述结论,证明了在折叠超立方体FQn(n≥3)中,若|Fe|+|Fv|≤2n−3,|Fe|≥1,且FQn中每个点至少关联两条无故障边,则在FQn−Fv−Fe中存在一个长度至少为2n−2|Fv|的圈．文献[9]证明了当|Fe|+|Fv|≤2n−4和|Fe|≤n−1时,Qn,k(n≥4)中能找到一条长为2n−2|Fv|的容错圈.文献[10]证明了当|Fe|≤2n−3且Qn,k中每个点至少关联两条无故障边时,若n和k有相同奇偶性,则Qn,k是偶泛圈的；若n和k有不同奇偶性,则在Qn,k中不仅可以构造长度从4到2n的偶圈,而且还存在长度从n−k+2到2n−1的奇圈．[11]证明当n和k有相同的奇偶性时,Qn,k(n≥3,1≤k≤n−1)是n−2-边容错超哈密顿脆弱的,也就是说,若|Fe|≤n−2,FQn−Fe中任意两个奇偶性不同的点之间存在一条长为2n−1的路．文献[4]研究了Qn,k的边泛圈问题,证明了在无故障加强超立方体Qn,k中,当n和k有相同奇偶性时,Qn,k中每一条边均在长度从4到2n−2的偶圈（即Qn,k是边偶泛圈的）；当n和k有不同奇偶性时,Qn,k中每一条边不仅均在长度从4到2n−2的偶圈上,而且还均在长度从n−k+2到2n−1的奇圈上．然而关于故障加强超立方体中容错边泛圈的嵌入问题目前还没有相关研究结果,本文对Qn,k的结构性质作了进一步探讨,并证明当|Fv|=1时,若n和k有相同奇偶性,则Qn,k中每一条边均在长度从4到2n−2的偶圈上；当n和k有不同奇偶性时,Qn,k中每一条边不仅均在长度从4到2n−2的偶圈上,而且还均在长度从n−k+4到2n−3的奇圈上.特别的,对于Qn,k中每一条j∈{k,k+1,···,n,c}−维边,它们还均在长度为n−k+2的奇圈上．同时还证明了当|Fv|≤n−2时,Qn,k(1≤k≤n−2)中每一条边均在长度从4到2n−2|Fv|的偶圈上．

2 定义和概念

文中没有说明的符号和定义参看文献[3].由于系统可以用图表示,我们经常用图的概念来表示网络的概念.G=(V,E)表示一个简单无向图,其中V为点集,E为边集.设x和y是图G中两顶点,连接x和y长度为k的xy路(path),记为xy路或是P[x,y],是指点和边交替出现的序列P=v0(=x)e1v1e2v2···vi−1eivi···ekvk(=y),且除点x和y外,其余的顶点互不相同,边ei的端点是vi−1和vi,x和y称为P的端点(end-vertices),其余的顶点称为内部点(internal vertices).P中边的数目k称为P的长度.两个端点相同的路称为圈(cycle).在简单图中,路P可以表示为P[v0,vk]=(v0,v1,v2,···,vk)．若v0=vk,则称P为圈(cycle)．包含图中所有顶点的路称为哈密顿路(hamiltonian path).包含图中所有顶点的圈称为哈密顿圈(hamiltonian cycle).图G中最短圈的长度称为G的围长(girth),记为g(G).图G中连接点u和v之间的最短路的长度称为两点间的距离(distance),记为dG(u,v).对于已知的图G,简记为d(u,v).图中任意两顶点u和v之间距离的最大值,称为图的直径(diameter),记为D(G).

如果图G含有长为l的圈,其中g(G)≤l≤v(G),g(G)是图G的围长,v(G)是图G的阶,称图G是泛圈的.如果图G是泛圈的,则一定是哈密顿的.网络是否具有泛圈性可以度量该网络是否可以嵌入任意长度的圈.泛圈性的概念被推广到点泛圈性和边泛圈性.如果图G的每个顶点位于长从g(G)到v(G)的圈上,则称G是点泛圈的(vertex-pancyclic).如果图的每条边位于长从g(G)到v(G)的圈上,则称G是边泛圈的(edge-pancyclic).显然,边泛圈的图一定是点泛圈的.因为二部图不含奇圈,故对二部图提出了偶泛圈的概念.如果图G含有长为l的偶圈,其中g(G)≤l≤v(G),称图G是偶泛圈的(even-pancyclic).如果图G中的任意两个顶点x与y之间长为l的路,其中dG(x,y)≤l≤v(G)−1且2|l−dG(x,y),则称G是偶泛连通的(even-panconnected).

n维超立方体Qn是一个简单图,其每个点x都可以用一个长为n的二元位串表示.即点集V(Qn)={x1x2···xn:xi={0,1},i=1,2,···,n}. 两个顶点相邻当且仅当它们对应的字符串中有且只有一位不同,即点x=x1x2···xn和y之间有边相连当且仅当y满足：中两个顶点x=x1x2···xn和y=y1y2···yn之间的Hamming距离定义为即表示两顶点的二元字符串中对应的不同分量的个数（或表示为dH(x,y)）．由定义可知,在Qn中dQn(x,y)=dH(x,y)．称连接u,ui之间的边(u,ui)为Qn中的i-维边,记Ei={(u,ui)|h(u,ui)=1,i∈{1,2,···,n}},因此

Qn,k作为超立方体的一种简单变型,它的顶点集和Qn的顶点集一样,只不过是通过在Qn中添加一些补边所得到的.它是这样定义的：

定义1加强超立方体Qn,k=(V,E)(1≤k≤n−1)是一个简单无向图.它和超立方体有一样的顶点集即V={x1x2···xn:xi=0 or 1,1≤i≤n}.两顶点x=x1x2···xn和y有一条边相连当且仅当y满足下列两个条件之一

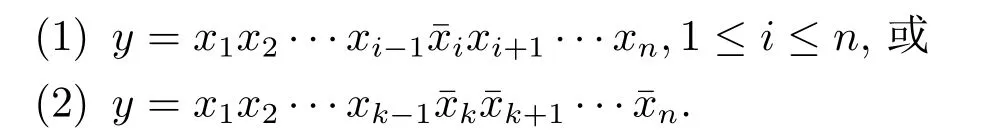
由加强超立方体Qn,k的定义可以看出加强超立方体Qn,k包含超立方体Qn作为它的子图.加强超立方体Qn,k是在超立方体Qn中添加2n−1条补边（the complementary edge）后得到的,即E(Qn,k)=Ec∪E(Qn),其中为补边集．边(u,ui)为Qn,k中的i-维超立方体的边,于是E(Qn,k)=Ec∪E1∪E2∪···∪En．

下面给出主要证明很重要的一些引理.

引理1(见文献[12]) 在超立方体Qn(n≥3)中,若fv≤n−2,则Qn中每一条无故障边均在长度从4到2n−2fv的圈上.

引理2(见文献[13]) 加强立方体Qn,k(1≤k≤n−1)能够沿着顶点的第i(1≤i≤n)个坐标将其分成两个子图.我们用分别来表示这两部分.一个点x=x1x2...xn属于当且仅当该点的第i位xi=0.同样地,一个点x=x1x2...xn属于当且仅当该点的第i位xi=1.当i

引理3(见文献[14]) 若fv≤n−2,则Qn中任意两相邻节点之间均存在长度从3到2n−2fv−1的奇长的路．

引理4(见文献[15])Qn(n≥3)中,任意两点u和v之间均存在长度为l的路,且dH(u,v)≤l≤2n−1,且l与dH(u,v)同奇偶.

引理5(见文献[16]) 如果|Fe|+|Fv|≤n−2,则Qn中任意两点u和v之间均存在长度为l的路,dH(u,v)+2≤l≤2n−2fv−1,且l与dH(u,v)同奇偶,其中fe表示Qn中故障边的数目,fv表示Qn中故障顶点的数目.

引理6(见文献[1]) 设u和v是Qn中任意两点,且dQn(u,v)=d,则在Qn中存在n条内点不交的路,其中d条长度为d,n−d条长度为d+2.

引理7(见文献[17]) 超立方体Qn(n≥4)中,当fv=n−1且Qn中每个点至少关联两个无故障点时,Qn中每一条边均在长度从6到2n−2fv的偶圈上．

引理8(见文献[15]) 超立方体Qn(n≥3)中每一条边均在长度从4到2n的偶圈上．

3 点容错下加强超立方体中边泛圈的嵌入

首先讨论当|Fv|=1时,若n和k有相同奇偶性,则Qn,k(n≥4)中每一条边均在长度从4到2n−2的偶圈上；若n和k有不同奇偶性,则Qn,k中每一条边不仅均在长度从4到2n−2的偶圈上,而且还均在长度从n−k+4到2n−3的奇圈上,特别的对于Qn,k中每一条j∈{k,k+1,···,n,c}-维边它们还均在长度为n−k+2的奇圈上,而对于Qn,k中每一条j∈{1,2,···,k−1}-维边则不能保证它们均在长度为n−k+2的奇圈上,例如Q4,3中的1-维边(0001,1001)就不在长度为n−k+2=3的圈上,2-维边(0101,0001)也不在长度为n−k+2=3的圈上,但长在为5的奇圈上,即0001→1001→1000→0000→0010→0001.

3.1 边偶泛圈嵌入加强超立方体

3.2 边奇泛圈嵌入加强超立方体

4 (n−2)-点容错下加强超立方体中边偶泛圈的嵌入

5 小结

网络是否具有泛圈性可以度量该网络是否可以嵌入任意长度的圈.加强超立方体是超立方体的变形结构,其连通性、安全性、可靠性以及传输延迟等性质都优于超立方体,对其性能和容错性的研究是非常重要的.本文主要探讨含有故障点的加强超立方体的边泛圈性.得到了如下结论

(1)当|Fv|=1时,若n和k有相同奇偶性,则Qn,k中每一条边均在长度从4到2n−2的圈上；当n和k有不同奇偶性时,Qn,k中每一条边不仅均在长度从4到2n−2的偶圈上,而且还均在长度从n−k+4到2n−3的奇圈上,特别的对于Qn,k中每一条j(∈{k,k+1,···,n,c})-维边它们还均在长度为n−k+2的奇圈上.

(2)当|Fv|≤n−2时,Qn,k中每一条边均在长度从4到 2n−2|Fv|的偶圈上．当n和k有不同奇偶性时,对含有更多故障节点和故障边的加强超立方体Qn,k的边奇泛圈性质的研究是下一步的工作.