嵌岩桩端部约束问题的辛弹性分析

姜忠宇，江 莉，赵 创

(1.安徽工程大学 建筑工程学院，安徽 芜湖 241000；2.安徽工程大学 力学重点实验室，安徽 芜湖 241000)

嵌岩桩以其低沉降、高承载力、工程适应性强等优点，在高层建筑、重型厂房及桥梁工程中得到了广泛的应用[1]。但由于其承载力大，试验耗费高，难以进行破坏性试验，制约了人们对嵌岩桩破坏模式的认识。而且桩基的性质多种多样，桩基强度取决于岩体强度、嵌岩深度与桩径等，因而桩基的破坏模式与承载力也有所不同，对不同桩基应有不同破坏模式[2]。张建新[3]等对嵌岩桩的荷载试验研究表明，嵌岩桩的破坏特性和桩身与桩周岩体的相对强度与刚度有关；当桩身承载力比基岩承载力低时，破坏发生在桩体；当桩身承载力比基岩高时，破坏发生在桩底基岩及桩与周围岩土界面上。因而，探究桩端处的应力与端部约束间的关系，对提高桩的承载力，改善端部应力分布有至关重要的影响。以往参考资料多从实验或数值模拟的角度分析端部约束效应，没有从理论上揭示其本质规律，给出合理的解释[4-6]。

目前尽管有许多精确且易于使用的有限元计算程序，使得嵌岩桩应力变形分析变得更加容易；但追求基本理论解依旧是工程技术人员坚持不懈努力的目标[7]。这是因为理论解可以为设计工程师提供一个宝贵的手段对数值分析结果进行评估，而且理论解可以更直观地揭示各变量之间的关系[8]。辛弹性力学通过将原来的位移变量与其对偶变量组成的状态空间引入弹性力学，完成了拉格朗日体系向哈密顿体系的过渡，从传统的欧几里得空间进入到了辛空间，使得对偶的混合变量方法进入到应用力学的广大领域[9]。应用辛弹性力学方法可以进行理性的推导求解，而不必采用传统的应力函数；针对端部复杂边界，只用圣维南原理予以覆盖的部分，也能推导出理论解[10]。

1 基本力学原理

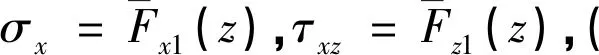
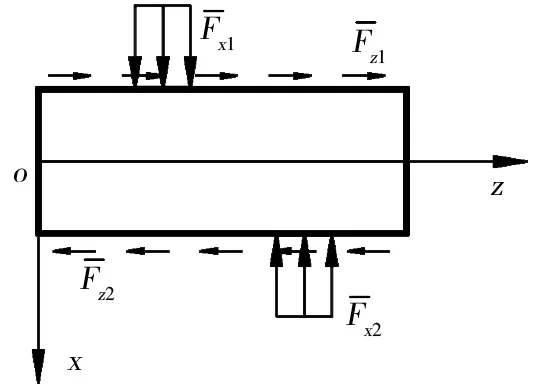
图1 平面矩形区域

根据平面弹性力学的静力平衡方程、几何方程和物理方程，得到哈密顿对偶方程组：

(1)

引入相空间向量v=(q,p)T，式(1)可以表示为

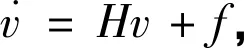
(2)

式中，H为哈密顿矩阵;f为非齐次项。

2 辛弹性力学求解

2.1 齐次方程的分离变量法

讨论算子的性质与外荷载无关，即先讨论式(2)的齐次线性微分方程

(3)

及齐次侧边界条件

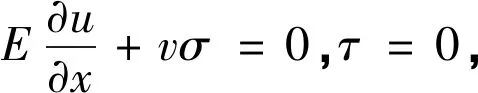
(4)

采用分离变量法求解，即令v(z,x)=ξ(z)ψ(x)，并将其代入齐次方程，可得ξ(z)=eμz和本征方程

Hψ(x)=μψ(x),

(5)

式中，μ表示沿z的本征值；ψ(x)表示本征向量。

该方程的本征解可分为两类，一类为零本征值的本征解(全局解)，它们不随坐标z的变化而衰减，是问题的基本本征解，对应的是圣维南问题的解(即边界条件通过等效形式提出)；另一类为非零本征值的本征解(局部解)，它们随坐标z的变化而衰减，对应的是圣维南原理所覆盖的部分(即严格满足边界条件下的解)。

2.2 零本征值的本征向量

由于哈密顿矩阵H不是对称阵，因此可能出现重本征值，而且还可以有约当型的本征向量。μ=0零本征解是一类特殊的解，有特殊的物理意义，代表了圣维南问题的解。约当型零本征值存在两条本征解链。

Hψ(x)=0,

(6)

基本本征向量和约当型本征向量

(7)

约当解并不是本征向量，对应原本征问题的本征向量实际上是

(8)

这6个零本征值的本征向量组成了一组共轭辛正交的向量组，每个本征向量都有相应的物理含义，这些本征解就是二维圣维南问题的基本解，可以张成一个完备的零本征值辛子空间。

2.3 非零本征值的本征向量

在讨论边界上的局部效应或域内有荷载突变时，零本征解就不能有效地描述问题了，这时需要更精确的解来描述边界效应，这就是非零本征解μ≠0。满足齐次方程和齐次侧边界条件的通解可直接求出[11]：

(9)

从结果中可以看出，A组、C组的解是对于z轴为对称变形的解，而B组、D组的解对于z轴为反对称变形的解。再根据方程存在非平凡解以及齐次侧边界条件，可以确定出A、B、C、D各组的系数。

(10)

非零本征值μn一般是复数，对于每个μn可以构造对应的本征函数，这些本征函数随着离开边界的距离而衰减，符合圣维南原理。解的构造如下：

vn=eμnzψn,

(11)

式中，μn是本征值；ψn是对应的本征向量。根据μ实部符号的不同，划分为两类：符号为正的α类解沿z轴的负方向衰减；符号为负的β类解沿z轴的正方向衰减，它们反映了不同端部的分布情况。

2.4 非齐次方程的特解

由于本征解之间存在辛正交归一关系，根据本征向量展开定理，将非齐次方程的非齐次项按本征解展开可得：

(12)

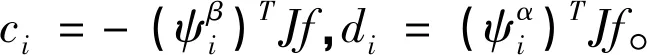
非齐次方程特解为

(13)

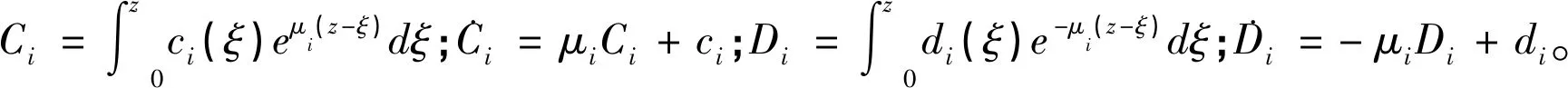
2.5 边值问题

方程的广义解由零本征解、非零本征解以及非齐次特解三部分构成[12]。

(14)

用Hamilton混合能变分原理求解待定参数ai。Hamilton混合能变分式为:

(15)

(16)

与圣维南原理不同的是，变分式从能量的角度给出了一个更加合理的边界条件。特别地，通过非零本征向量的引入，在固定端附近的位移和应力分布可以得到更加精确的分析结果。

将式(14)代入式(16)，可以得到关于δai的变分方程，对于任意的δai都成立，由此得到一个关于ai的N维线性方程组[13]：

(17)

表达式中的矩阵元素为

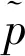
3 模型计算及实例

嵌岩桩的直径1 m、长度10 m，桩底进入持力层深度0.8 m，土层与持力层的交界面即为岩-土交界面。桩身材料选用C30混凝土，其弹性模量30 GPa，泊松比0.2；粘土层的容重γ=18.4 kN/m3，泊松比vr=0.38。

嵌岩桩受力简图如图2所示。桩侧压力沿桩长按线性变化。静止水平侧压力系数K0=0.45，荷载集度qz=K0γh=82.8 kN/m，桩侧摩阻力荷载集度qt=25 kN/m。桩顶竖向线荷载Pd=4×103kN/m。

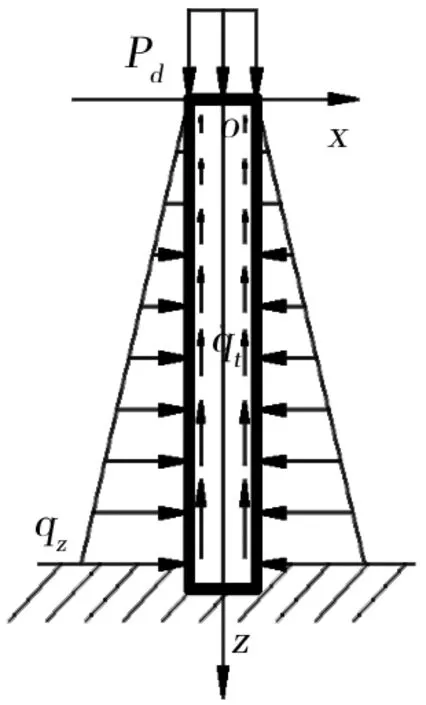
图2 嵌岩桩的受力图

依据计算参数分别采用有限元ANSYS软件和辛弹性力学方法在Matlab中进行求解。用辛弹性力学方法计算的嵌岩桩位移场和应力场云图如图3所示。为作比较给出了ANSYS计算的有限元结果如图4所示。通过对比可以看出，两种方法均能对嵌岩桩力学问题进行全面的分析，且计算结果基本一致，云图分布大体相同(桩身处云图的差异是由于两种方法色带选取不同造成的，不影响计算数值)，保证了辛算法计算结果的可靠性。

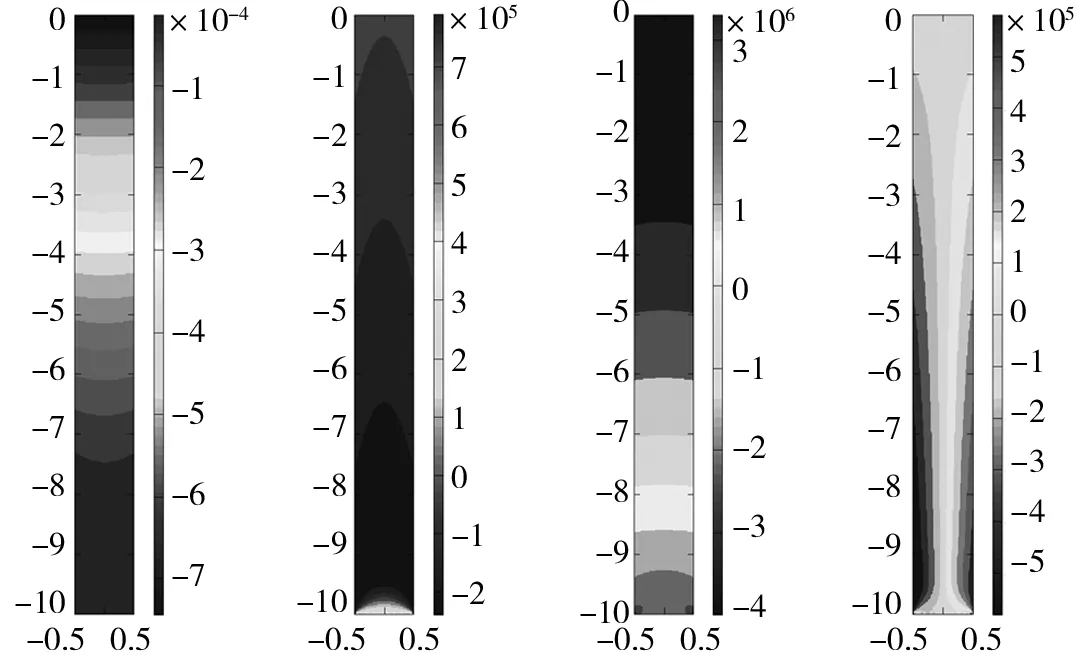
图3 辛弹性力学计算的嵌岩桩位移场和应力场

图4 有限元方法计算的嵌岩桩位移场和应力场

进一步详细地绘制了两种方法在嵌岩桩岩-土交界面处的应力值如图5、图6、图7所示。由图5、图6、图7比较可以看出，两种方法的变化趋势一致，在边角处应力值都有较大突变，这正与工程实际中的角点处应力集中现象相吻合。图5～图7中辛弹性力学解答的波动主要是截取非零本征向量数目造成的，随非零本征向量数目的增加，曲线将趋于平滑。辛算法不仅能准确地计算出问题的全局解，也能合理有效地处理边界条件得到问题的局部解，在全场范围内对问题进行精确、可靠的分析。

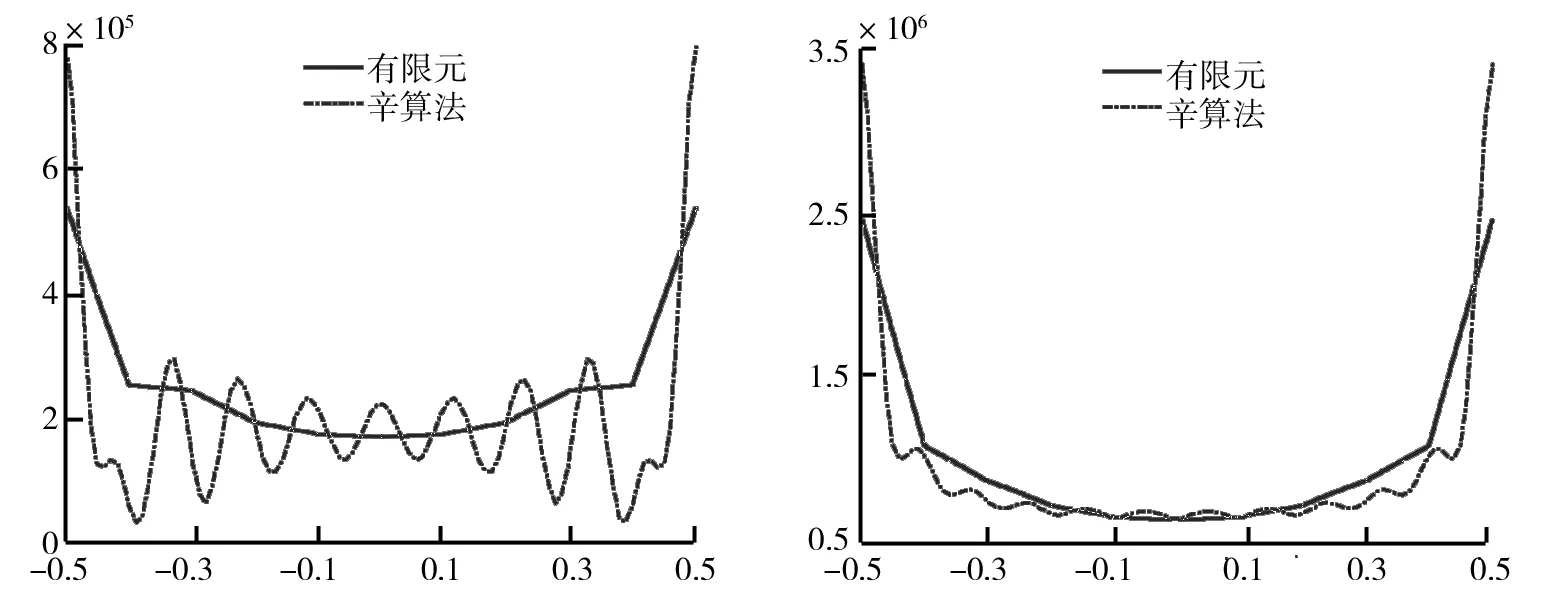
图5 比较两种算法在岩-土交界面处的σx 图6 比较两种算法在岩-土交界面处的σy

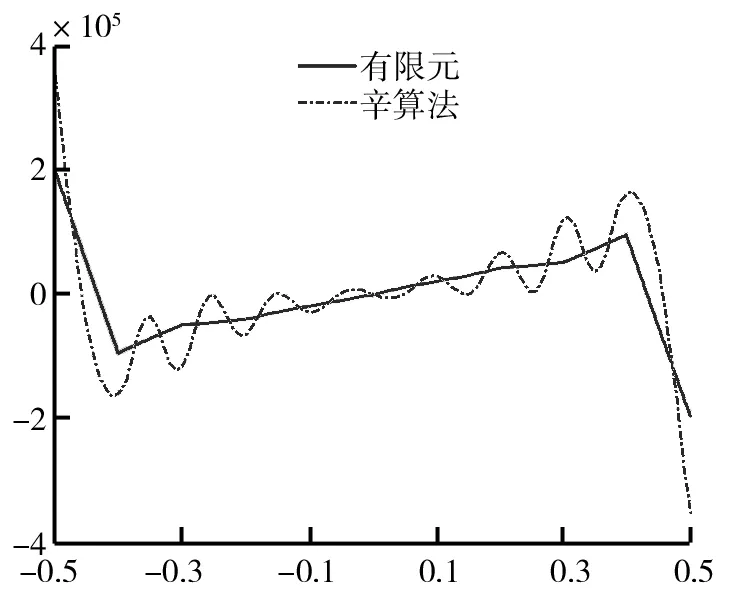
图7 比较两种算法在岩-土交界面处的τxy

4 结论

传统弹性力学解析法通常采用圣维南原理，将复杂边界条件通过静力等效形式提出，虽然可以准确地计算出弹性体的全局解，却无法计算出严格满足边界条件的局部解，这使得弹性体在边角处的应力数值与工程实际不相符。辛弹性力学有别于传统的逆解法和半逆解法，它能够在严格满足边界条件的基础上，计算出圣维南原理所覆盖部分的解(这部分解正是传统方法所缺失的解)，通过一步步地理论推导得到最终结果，它更加深刻地揭示弹性问题的本质。通过算例证实了辛方法是一种合理、有效的解析方法，为解决平面矩形域问题提供了一套新的理论方法。

利用辛算法可以计算出平面矩形域的基本本征向量，这些基本本征向量张成一个完备的零本征值辛子空间，再根据具体的两端边界条件，确定零本征向量和非零本征向量的待定系数，最后叠加上非齐次问题的特解，即可求出嵌岩桩端部约束问题的精确解。算例中辛算法精确地描绘出嵌岩桩在土-岩交界面处的应力分布情况，其计算结果与有限元软件模拟结果一致。这为深入研究嵌岩桩的破坏模式、提升承载力等，提供了新理论、新思路。

辛算法的不足之处在于计算推导过程繁琐，仅能计算一些规则区域、简单边界的特殊问题，对于一般工程问题适用性差。有限元法是一种数值算法，适用性强，它把复杂的整体结构离散为有限个单元体，在单元内用形函数插值近似表达单元内部任意一点的结果，缺点是无法准确找出各个变量之间的相互关系，两种方法如能有机结合，则对解决工程实际问题大有帮助。