加热卷烟加热元件温度场分析及试验研究

时春鑫，郑绪东，吴建德，李志强，王程娅，王 汝，马 军

1. 昆明理工大学信息工程与自动化学院，昆明市呈贡区景明南路727 号 650500

2. 云南中烟工业有限责任公司技术中心，昆明市五华区红锦路367 号 650231

加热元件作为加热卷烟加热装置的核心部件，其性能的优劣决定了加热装置能否最大化利用热能，充分加热烟支，提高电池的使用效率。因此，研制高性能的加热元件和小型化电池具有重要意义。目前加热卷烟的研究主要集中在卷烟制备及烟气释放物等方面，有关加热装置特别是加热元件的研究报道较少［1-3］。加热元件主要有周向（环绕）加热、中心加热和环绕-中心组合加热等模式［4-6］，根据材质的不同又可分为金属加热元件和非金属加热元件两种。金属加热元件包括镍铬丝（Ni-Cr）、铁铬铝丝（Fe-Cr-Al）和镍铁丝（Ni-Fe）等材质，非金属加热元件包括PTC（Positive Temperature Coefficient）电热元件，碳化硅、硅钼棒和厚膜加热元件等，其中厚膜加热元件是加热卷烟最常用的加热方式。加热装置的工作状态包括预热和恒温两种模式，预热模式下加热元件迅速升温至目标值，烘烤发烟基质使其产生可供抽吸的烟气；恒温模式下加热元件保持恒定的温度烘烤发烟基质，使其产生稳定的烟气。

菲利浦·莫里斯烟草国际公司的代表性产品IQOS 是目前世界上销售范围最广的加热卷烟，其工作温度不超过350 ℃［7-9］。英美烟草公司的代表性产品GLO，采用“FPC（Flexible Printed Circuit）+薄不锈钢管”周向加热方式，整个加热体分为上下两段，工作温度基本保持在200～250 ℃之间。而目前国内加热装置加热元件的开发多以经验为主，缺乏基础性理论研究，导致加热装置存在温度波动大、烘烤烟支口感差等问题。研究发现，加热卷烟的加热温度在250～350 ℃之间［8-10］，根据现有发烟基质的属性，预热模式下加热元件需要快速升温至300～350 ℃，恒温阶段则保持在300～320 ℃。为此，根据加热装置温度控制需求，结合加热元件基本电学性能，设计了一种温度控制电路，并建立了热-电耦合作用下加热元件的数学模型，利用有限元方法对加热元件的温度场分布进行分析，通过搭建试验平台验证仿真结果，以期为加热元件的研发提供技术支撑，进一步提升加热卷烟加热装置的整体性能。

1 试验电路

1.1 温度控制原理

使用陶瓷加热元件电阻温度特性测试系统（MRT-10），选取4 片以氧化铝陶瓷为基底材料、铂基电阻浆料为导电轨迹、金属银为焊盘和引脚材料的加热元件，进行加热元件RL阻值与温度关系测试，结果见表1。可见，25 ℃时，加热元件RL阻值相对误差＜3%；320 ℃时，加热元件RL阻值相对误差＜5%，表明加热元件RL阻值稳定性较好。由公式V=I×R 可知，在恒温过程中，加热元件两端电压V 恒定，电流I 自稳定到固定值，实现加热元件温度恒定。由公式P=I2× R 可知，当加热元件温度大于设定值时，通过加热元件的电流I 会减小，加热元件两端功率P 降低，加热元件温度降低；当加热元件温度小于设定值时，则通过加热元件的电流I 增大，加热元件两端功率P 增大，加热元件温度升高。根据表1 中数据进行验证可得到电压规律：在3.4 V 电压下，加热元件从25 ℃预热到300 ℃以上时，预热时间约为10 s，电流从约2.8 A 降低至约1.4 A；在2.5 V 电压下，当恒温至310 ℃时，电流约为1.05 A。

表1 25 ℃和320 ℃条件下RL阻值Tab.1 Resistance of RL at 25 ℃ and 320 ℃

根据以上控制参数，在设计温控电路时，先采用电压值高的恒压源模块使加热元件快速升温到预期温度，当温度达到预期值后采用电压值低的恒压源模块稳定加热温度［11］。图1 中，模块1 为启动感应模块，用于启动系统上电（K1 闭合）。模块2 为输出控制模块，当系统上电时，K2 与上端接通，红色指示灯亮，1#恒压源输出3.4 V 电压为加热元件RL供电；当加热元件快速加热升温至设定值时，4#比较器输出信号使K2 切换至与下端接通，2#恒压源输出约2.5 V 电压为加热元件RL供电，绿色指示灯亮，此时加热元件两端电压稳定，达到温控要求。模块3 为运算及显示控制模块，通过4#比较器控制3#切换开关的切换及6#指示灯电路的显示。

图1 温度控制原理框图Fig.1 Block diagram of temperature control principle

1.2 温度控制电路设计

如图2 所示，温度控制电路可以通过调节R1～R4 阻值各提供 1 个 3.4 V 和 2.5 V 恒压源，分别用于预热模式和恒温模式。加热装置的工作模式分为休眠、预热和恒温3 种。休眠模式中，当微控制器 IO1=0、IO2=0 时，三极管Q3、Q4 均不工作，MOS 管 Q1、Q2 关断，此时加热元件 RL上的电压恒定为0。预热模式中，当微控制器IO1=1、IO2=0时，三极管 Q3 导通、Q4 断开，MOS 管 Q1 闭合、Q2断开，3.4 V 恒压源为加热元件供电，加热元件快速升温，加热元件RL的阻值从1.2 Ω上升至2.4 Ω。恒温模式中，当微控制器IO1=0、IO2=1 时，三极管Q3 断开、Q4 导通，MOS 管 Q1 断开、Q2 闭合，2.5 V 恒压源为加热元件供电，保持加热元件温度稳定。

图2 温度控制电路图Fig.2 Temperature control circuit diagram

2 加热元件温度场仿真分析

2.1 几何模型

加热元件一般由基底和发热电路（包括丝印层、焊盘、引线）组成。发热线路在电压的激励下产生焦耳热，瞬态情况下可用方程（1）和方程（2）描述，式中的电导率σ是随温度变化的函数；加热元件的瞬态传热过程可用方程（3）描述，将方程（2）代入方程（3）的热源项Q，即可得到加热元件的温度分布。

式中：Δ为哈密顿算子；σ为电导率，1/(Ω·m)；T 为温度，K；Je为外部电流密度，A/m2；∂D/∂t 为位移电流密度，A/m2；J 为电流密度，A/m2；E 为电势，V，Qj为初始存在的体电流；ρ为工件密度，kg/m3；C为材料恒压热容，J/(kg·K)；k为热传导系数，W/(m·K)。

由图3 可见，加热元件的基底材料为氧化铝陶瓷，丝印层材料为铂基电阻浆料，焊盘及引脚材料均为金属银；基底长度20 mm，前端宽度5 mm，后端宽度7.5 mm，厚度0.5 mm，丝印层厚度30 μm。为便于表征加热元件温度场分布特性，本研究中将加热元件分为前中后3 段。

加热元件相关材料热力学参数见表2。可见，各参数随着温度变化均呈非线性变化。此外，金属银的恒压热容为230 J/(kg·K)，密度为10 500 kg/m3，导热系数为420 W/(m·K)。

图3 加热元件模型及其几何尺寸图Fig.3 Heating element model and its geometric dimensions

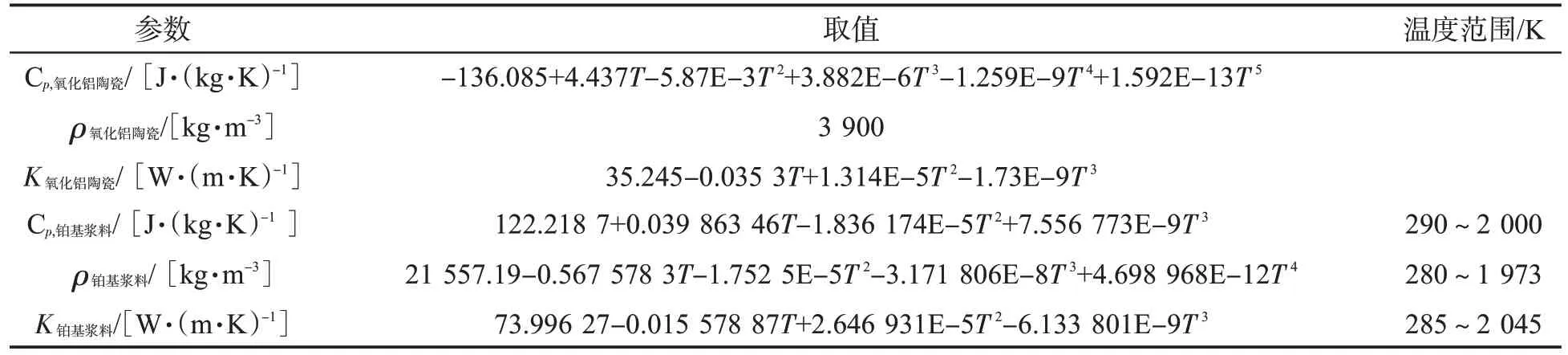
表2 加热元件相关材料热力学参数Tab.2 Thermodynamic parameters of materials related to heating elements

2.2 边界条件及载荷

将上述模拟电路的输出电压通过内插函数的方式加载在负载两端，电流经过加热元件时产生焦耳热，一部分通过热对流、热辐射的方式传递到空气中，另一部分用于加热升温加热元件。运用多物理场有限元仿真软件COMSOL Multiphysics模拟加热元件内部的热-电耦合作用，电流经过加热元件时产生的焦耳热使加热元件温度升高，进而引起材料参数发生变化［12］，并改变发热电路内部电场，具体形式见图4。设置环境温度为25 ℃，湿度为59%，加热元件引脚处的热传导可通过傅里叶传热方程描述［13］，引脚处的温度响应曲线见图5。

2.3 结果分析

图4 多物理场耦合求解Fig.4 Multi-physics coupling solution

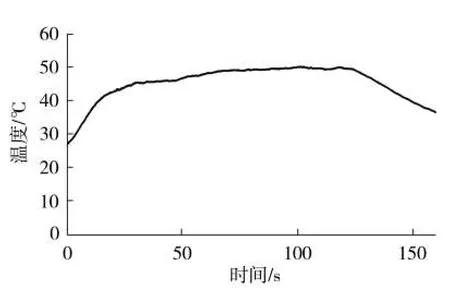
图5 加热元件引脚处温度响应曲线Fig.5 Temperature response curve at the pin

由图6 可见，预热模式下，温度控制电路的3.4 V 恒压源工作10 s，加热元件温度迅速上升至343 ℃；恒温模式下，温度控制电路的2.5 V 恒压源工作110 s，加热元件温度下降一定幅度后最终稳定在312 ℃；休眠模式下，加热元件温度迅速下降。结果表明，该模型能够较好地模拟加热元件整个工作过程且满足控制需求。

图6 加热元件温度最大值响应曲线Fig.6 Maximum temperature response curve of heating element

由图7 可见，预热模式下，加热元件温度随加热时间的延长呈非线性变化，且自前段至后段呈梯度分布，高温区域集中于前段，低温区域集中于后段。总体上，加热元件温度增加速度随加热时间的延长而逐渐缓慢，但前段温度增加速度始终大于后段增加速度。由图8 可见，恒温模式下，加热元件温度自前段至后段亦呈梯度分布，前段温度＞280 ℃，中段温度＞180 ℃，后段温度＞120 ℃。

图7 预热模式下加热元件温度分布云图Fig.7 Cloud diagram of heating element temperature distribution in preheating mode

图8 恒温模式下加热元件温度分布图Fig.8 Temperature distribution diagram of heating element in constant temperature mode

由图9 可见，加热元件温度最大值、平均值和最小值的变化趋势相同，均为在预热模式下快速增加，在恒温模式下趋于恒定。恒温模式下，加热元件温度最大值为312 ℃，平均值为223 ℃，最小值为128 ℃。此外，加热元件温度最大值与最小值的差值亦呈现先增加后减小趋势，最大差值为229 ℃且最终稳定在184 ℃。

为进一步了解加热元件温度分布，对加热元件前中后3 段的中心点（分别简称FSC、MSC、BSC）温度以及各点之间的温度差进行分析。由图10 可见，预热模式下，各点之间的温度差均随加热时间的增加而增大；恒温模式下，各点之间的温度差均随加热时间的增加而减小，并最终分别稳定在 301、237 和 147 ℃。MCS 与 BCS 之间的温度差比FCS 与MCS 之间的温度差大，表明加热元件在中后段的温度梯度较大。

图9 加热元件温度最大值、平均值、最小值温度响应曲线以及最大值与最小值差值Fig.9 Maximum, average and minimum temperature response curves of heating element and the difference between maximum and minimum temperatures

图10 加热元件FCS、MCS、BCS 温度响应曲线以及FCS、MCS、BCS 温度差Fig.10 Temperature response curve of FCS, MCS and BCS of heating element and temperature difference between FCS, MCS and BCS

3 试验测试

3.1 试验设计

由图11 可见，试验平台包括FLIR T420 红外热成像测试仪（精度±2%，分辨率320 PPI×240 PPI，热灵敏度＜0.045 ℃，美国菲力尔公司）；多功能测温装置（云南中烟工业有限责任公司技术中心深圳研创平台自制）；DK-601 型多功能电子温湿度计（分辨率0.1 ℃/1%，温度误差≤±0.8 ℃，相对湿度误差≤±5%，北京思创远洋科技有限公司）；计算机（操作系统Windows10，处理器Inter(R) Core(TM) i5-7500，内存8G DDR4）。

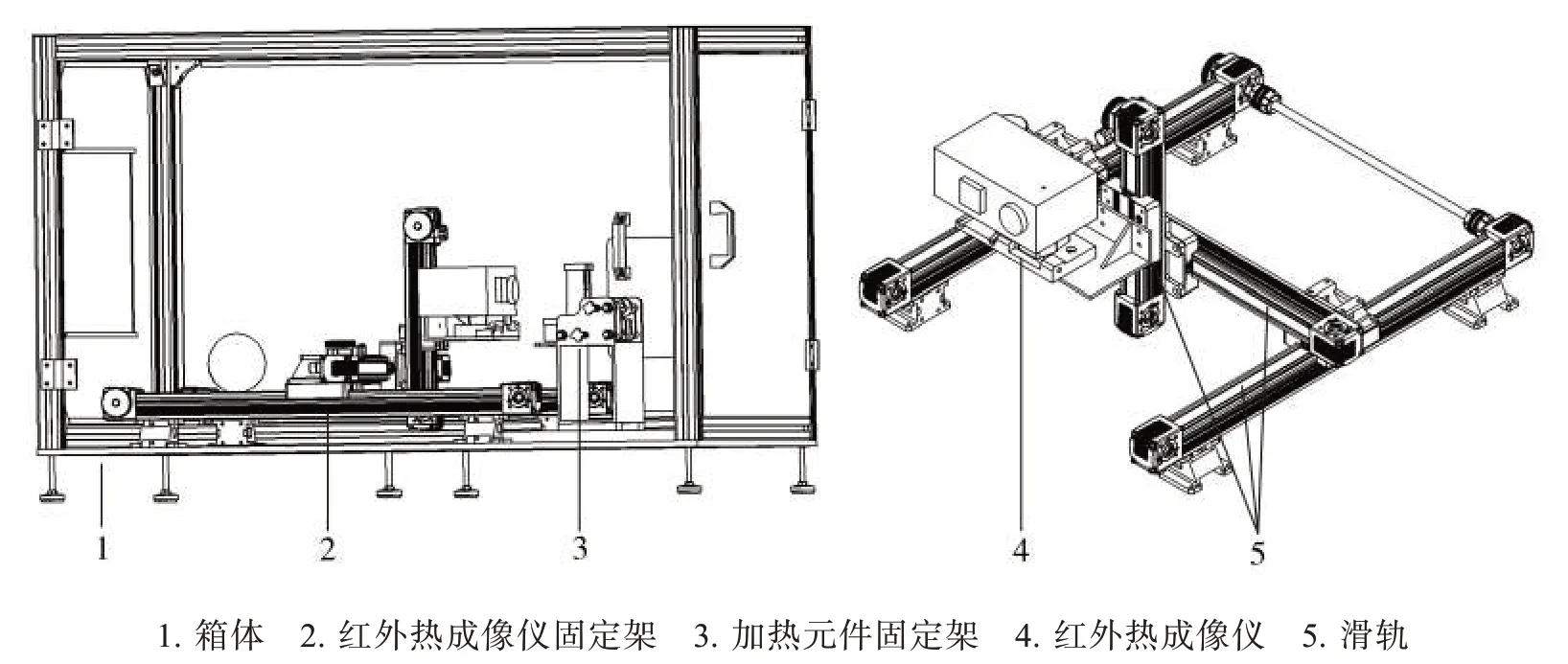
图11 测试平台结构示意图Fig.11 Test platform structure diagram

将红外热成像仪安装于多功能测试箱内部的红外热成像仪固定架上，通过数据线将其与计算机连接；将加热元件垂直放置于红外热成像仪正前方的加热元件固定架上，并通过滑轨对红外热成像仪的焦距进行调节，启动加热装置；记录加热元件温度最大值、前中后段中心点温度并绘制温度响应曲线。红外热成像仪温度设置范围为0～650 ℃，辐射率设置为0.9，环境温度为（25±2）℃，相对湿度为（56±5）%。

3.2 数据分析

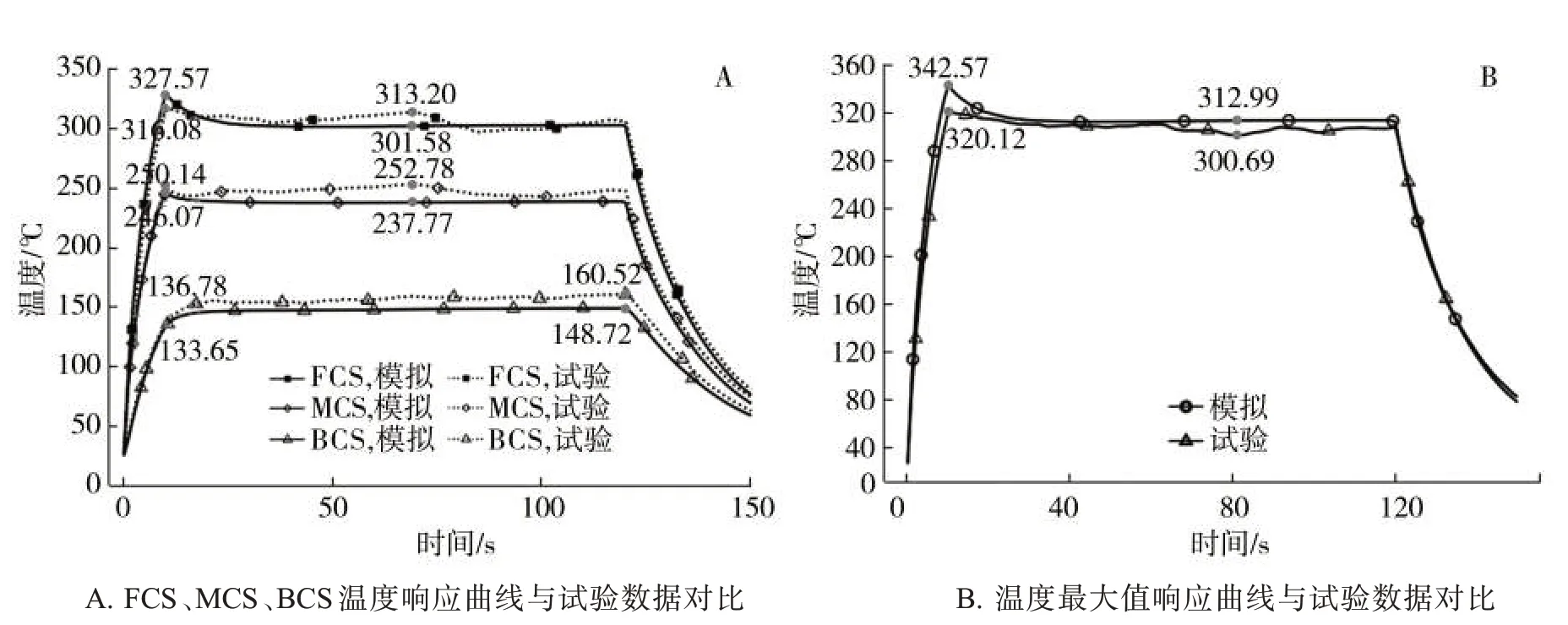
图12 FCS、MCS、BCS 温度及温度最大值响应曲线与试验数据对比Fig.12 Comparison of response curves of FCS, MCS, BCS and maximum temperature with test data

由图 12 可见，预热模式下，FCS、MCS、BCS 温度响应曲线与试验数据对比的最大误差分别为4.0%、1.7%和2.4%；恒温模式下，FCS、MCS、BCS温度响应曲线与试验数据对比的最大误差分别为3.9%、6.4%和8.3%。此外，预热模式下，加热元件最高温度试验值与模拟值最大误差为4.8%；恒温模式下，加热元件最高温度试验值与模拟值最大误差为7.1%。可见，模拟结果与试验结果具有较高一致性，验证了加热元件有限元仿真模型的正确性。

4 结论

根据加热卷烟加热元件的温度控制要求设计了一种温控电路，并建立了加热元件在热-电耦合作用下的三维模型，通过模拟仿真获得加热元件温度随加热时间呈非线性变化，且前段至后段呈梯度分布的变化特性。利用搭建的试验平台对该模型进行验证，结果表明：预热模式下，加热元件最高温度模拟值与试验值的最大误差为7.1%；恒温模式下，加热元件最高温度模拟值与试验值的最大误差为4.8%。模拟结果与试验结果具有良好一致性，且误差在可接受范围内，验证了该模型及仿真方法的有效性。后续将继续对不同加热元件（棒式、杯式、电磁式等）的温度场分布进行研究，进一步优化加热元件的尺寸、结构和材料属性，解决现有温控系统存在控制延迟、精度低等问题，以提升加热卷烟加热装置的整体性能。