特征定量识别的航天精密伺服机构轴承运行可靠性评估方法及应用

袁 静，李 昕，魏 颖，蒋会明，赵 倩，刘海江

（1.上海理工大学 机械工程学院，上海 200093；2.上海无线电设备研究所，上海 201109；3.同济大学 机械与能源工程学院，上海 201804）

0 引言

精密伺服机构广泛应用于卫星通信、相对导航、深空探测、遥感遥测等航天领域，以实现天线结构支撑与姿态变换驱动。航天精密伺服机构的性能要求日趋精密化、轻量化、智能化，使得伺服机构的机械可靠性问题日益突出，呈现出故障多样化，失效模式与破坏机理均异于传统机械等［1］。同时，航天产品复杂载荷和极端环境使得精密伺服机构的可靠性评估更具挑战性。滚动轴承是精密伺服机构中的关键运动副，其可靠性常作为表征航天精密伺服机构寿命的重要指标。由于受到润滑可靠性与异常冲击等影响，滚动轴承容易发生磨损、疲劳、压痕、胶合，甚至断裂等，导致机构传动系统性能降低或功能丧失。因此，精密伺服机构的轴承动态可靠性关系到服役产品综合性能与质量可靠性。

传统的可靠性评估方法以概率与数理统计为数学基础，以获得同批次设备共性的平均可靠性。航天精密伺服机构等单台精密设备的可靠性，大多采用样机在模拟工况下的1∶1 实时寿命试验或加速寿命试验来验证考核。其中，美国多家研究单位在航天机构轴承可靠性评价中，以威布尔分布为理论基础并依据任务时间考核验证试验进行轴承寿命定性评估［2］。这样的单机寿命试验价格昂贵，费时费力［3］，却难以精确评估所关心的正样产品真实可靠性。

为弥补传统可靠性评估方法不足，学者们开始从设备性能退化监测［4-5］、模糊可靠性［6］、故障预测［7-8］等方向提出小样本条件下的可靠性评估新方法。然而，这些可靠度建模手段依旧依赖历史样本数据和先验知识。相比设计可靠性、制造可靠性等固有属性，人们往往更关心当下具体设备的真实运行的可靠性，它受到服役工况、运行时间、零件性能退化与故障失效等诸多客观因素影响。因此，针对某台具体设备运行可靠性评估的个性问题，基于状态信息的运行可靠性评估方法［9］孕育而生，并在工程实践中取得了良好的应用效果。针对航天精密伺服机构轴承运行工况复杂且缺乏合理可靠性研究方法，本文将基于状态信息的运行可靠性评估方法引入到航天机构轴承服役寿命研究中。以某航天产品精密伺服机构轴承为研究对象，综合利用表征设备运行品质的动态信号，采用自适应标准多小波包解调分析［10］与冲击脉冲法定量识别机构关键轴承运行状态特征，并基于降半正态分布隶属函数构建关键轴承运行状态特征与运行可靠度的归一化区间［0，1］的关联映射模型［11］，从而实现航天精密伺服机构轴承的运行可靠性评估，确保航天产品局部核心机械可靠性，为精密伺服机构轴承可靠性评估缺乏大样本数据和当下产品可靠度难以真实评价的工程难题开辟新途径。最后，通过轴承试验台和某型精密伺服机构轴承可靠性研究的应用案例，验证该方法的有效性与实用性。

1 基于自适应标准多小波的滚动轴承特征定量识别技术

新兴多小波变换是小波理论新的发展方向。多小波兼备多种优良性质与多个时频特性差异的基函数，通过矢量内积实现故障特征提取与识别，工程应用效果明显优于经典小波、二代小波等［12-13］。由于受到基函数构造和能量误差传播等因素影响，传统多小波变换存在明显的故障特征幅值失真现象，无法实现精密伺服机构轴承状态特征定量识别。为提高轴承运行可靠性评估精度，将自适应标准多小波基函数引入到滚动轴承特征定量识别中。标准多小波继承传统多小波变换的优点，兼备正交性、对称性、高阶消失矩与能量守恒等优良特性，为精密伺服机构轴承状态特征提取的准确性、全面性和定量性提供基础。以对称正交多小波构造条件为约束，标准多小波基函数中低通滤波器{Gk，k=0，1，2，3}和高通滤波器{Hk，k=0，1，2，3}可构造［10］为

式中：自由参数a∈[-1，1]且b=±1；转换矩阵。

在自适应多小波优选中，采用融合归一化能量熵指标、归一化奇异熵指标和峭度指标的多目标优选技术［10］，优选出与轴承动态信号相匹配的最佳标准多小波基函数。

冲击脉冲法是一种有效的滚动轴承状态监测与损伤评价手段，采用只与轴承工作状态有关的标准分贝值dB 表征轴承不同故障状态下的冲击值增加率，以评价滚动轴承正常状态、早期故障、严重故障和失效4 种运行状态［14］。本文结合自适应标准多小波包解调分析，获得精密伺服机构轴承特征频率所对应的真实幅值，再利用脉冲冲击法对解调结果进行量化评价，为后续机构轴承运行可靠性评估提供准确的运行状态定量信息。具体方法归纳为如下步骤：

步骤1根据式（1）和式（2）构造标准多小波库{Gk}和{Hk}。

步骤2对待测信号s进行严格采样的预处理以获得矢量输入信号u0。

步骤3采用式（3）的多小波包变换进行l层分解，并后处理{uj，1≤j≤2l}获得标准多小波分解系数{uj，1≤j≤2l}，

步骤4采用多目标优选技术［10］获得与待测信号s相匹配的最佳标准多小波{Hk}opt和{Gk}opt，其中最佳参数为aopt和bopt。

步骤5以最佳标准多小波重复步骤3～步骤4获得最佳标准多小波分析结果{uj，1≤j≤2l}opt，并进行Hilbert 包络解调分析获得不同频带的包络谱。

步骤6根据精密伺服机构转频与轴承尺寸等信息，分别计算得到轴承内圈、外圈、滚动体与保持架特征频率fi、fo、fb、fc［15］。

步骤7采用式（4）分别计算自适应标准多小波包解调分析中fi、fo、fb、fc处轴承内圈、外圈、滚动体与保持架特征指标Fi、Fo、Fb、Fc，并将其中最大值作为轴承特征定量识别指标F，

式中：n为转速；d为轴承内径；Ht为自适应标准多小波包解调分析结果的冲击值。

步骤8依据自适应标准多小波包解调分析结果的标准分贝值，按照如下的冲击脉冲法评判准则［14］量化评估轴承运行状态：

2 基于特征定量识别的精密伺服机构轴承运行可靠度建模

为将自适应标准多小波包解调分析与脉冲冲击法定量提取精密伺服机构轴承运行状态信息映射至运行可靠度的归一化区间［0，1］之间，利用隶属度函数构建了轴承运行隶属可靠度。本文应用基于尾部修正的降半正态分布隶属函数映射到归一化区间［0，1］之间，获得基于轴承特征定量识别指标F的轴承运行可靠度模型R(F)［11］：

式中：FA、FB和FC为子集范围；参数m为常数。

依据式（5）设定隶属可靠度判定标准，首先在正常状态和失效模式下，轴承运行可靠度分别为1和0，即获得FA=0 dB，FB=21 dB，FC=60 dB；其次，在早期故障和严重故障状态下，轴承运行可靠性退化呈现为降半正态分布曲线。其中，以早期和严重故障的临界值F=35 dB 作为隶属可靠度0.5的临界状态［11］，即，获得参数m=0.003 5。因此，基于特征定量识别的精密伺服机构轴承运行可靠度建模可定义为

3 轴承试验台数据分析

某轴承试验台由转速控制箱、交流伺服电机、传动轮、联轴器、转轴、动平衡质量盘与加载装置等组成。同时，采用电火花加工技术在滚动轴承N205外圈表面预置模拟故障，如图1 所示。加速度传感器安装于故障轴承支承座上，试验中轴承转速为470.3 r/min，即7.84 Hz，信号采样频率为12.8 kHz。根据滚动轴承N205 尺寸参数与转速计算得到外圈特征频率fo=39.24 Hz，对应特征周期0.025 s。

图1 滚动轴承N205 外圈故障Fig.1 Outer-ring fault of rolling bearing N205

所采集到的时域信号及其频谱如图2 所示。从图中可以看到，时域信号存在明显的以0.025 1 s 为间隔的周期性冲击（部分标记为红色三角形），且频域信号中高频部分也出现边频带特征，可判断该轴承外圈故障处于中晚期较为明显的损伤阶段。为评估该轴承的运行可靠性，采用自适应标准多小波的滚动轴承特征定量识别技术对图2 信号进行分析，多小波包分解层数l=3，优化得到的自适应标准多小波基中最佳参数为aopt=0.986 8 和bopt=1，轴承外圈特征频率最大分贝值所对应的Hilbert 包络解调结果如图3 所示。图中轴承外圈特征频率fo及其倍频格外清晰，根据式（4）计算得到轴承外圈特征定量识别指标Fo=35.06 dB。依据式（5）的评判准则，该轴承外圈故障处于早期和严重之间，与图1 所示的明显外圈损伤符合。将该指标代入轴承运行可靠度模型中，计算得到该轴承运行可靠度指标R（35.06）=0.500 5。

图2 轴承试验台振动信号Fig.2 Vibration signals of the bearing test-bed

图3 图2 信号的自适应标准多小波包解调结果Fig.3 Envelope demodulation result of the adaptive standard multiwavelets for signals in Fig.2

4 工程应用

将本文方法应用到某型航天精密伺服机构的轴承测试与评估中。该机构传动链末级采用686 微型滚动轴承。在末级传动链轴承座上安装加速度传感器采集该轴承振动信号，测试中伺服机构驱动天线以转频fr=2 Hz 在转角+40°～-40°范围内进行近似匀速摆动，采样频率2 000 Hz。根据轴承尺寸参数与转频计算得到fi=9.68，fo=6.32，fb=4.54，fc=0.79。

所采集到的一组轴承振动信号及其频谱如图4所示。其时域信号表现为典型周期性冲击信号，根据冲击时间间隔可推知该冲击为伺服机构摆动中瞬时换向所产生的撞击，且频谱中无明显轴承特征相关频率。采用本文方法对该轴承进行运行可靠性评估，多小波包分解层数l=2，优化得到的自适应标准多小波基中最佳参数为aopt=0.696 8 和bopt=1，4 个频带的自适应标准多小波包解调分析结果如图5 所示。从图5 中可以看到，轴承转频fr格外清晰，而轴承特征频率fi、fo、fb和fc并不明显。根据式（4）计算得到轴承内圈、外圈、滚动体和保持架特征指标Fi=7.18 dB，Fo=7.89 dB，Fb=8.15 dB，Fc=5.73 dB，如图6 所示。这些指标均低于21 dB，说明轴承无故障。将上述指标最大值作为轴承特征定量识别指标F=8.15 dB，并代入轴承运行可靠度模型，计算得到该轴承运行可靠度R（8.15）=1，说明该航天精密伺服机构滚动轴承运行安全可靠。

图4 某航天精密伺服机构轴承振动信号Fig.4 Vibration signals of the bearing of an aerospace precision servo mechanism

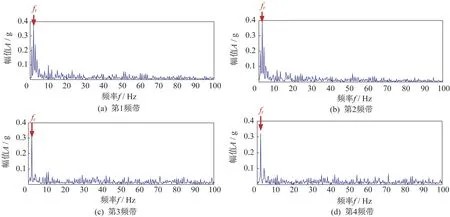
图5 图4 信号的自适应标准多小波包解调结果Fig.5 Envelope demodulation results of the adaptive standard multiwavelets for signals in Fig.4

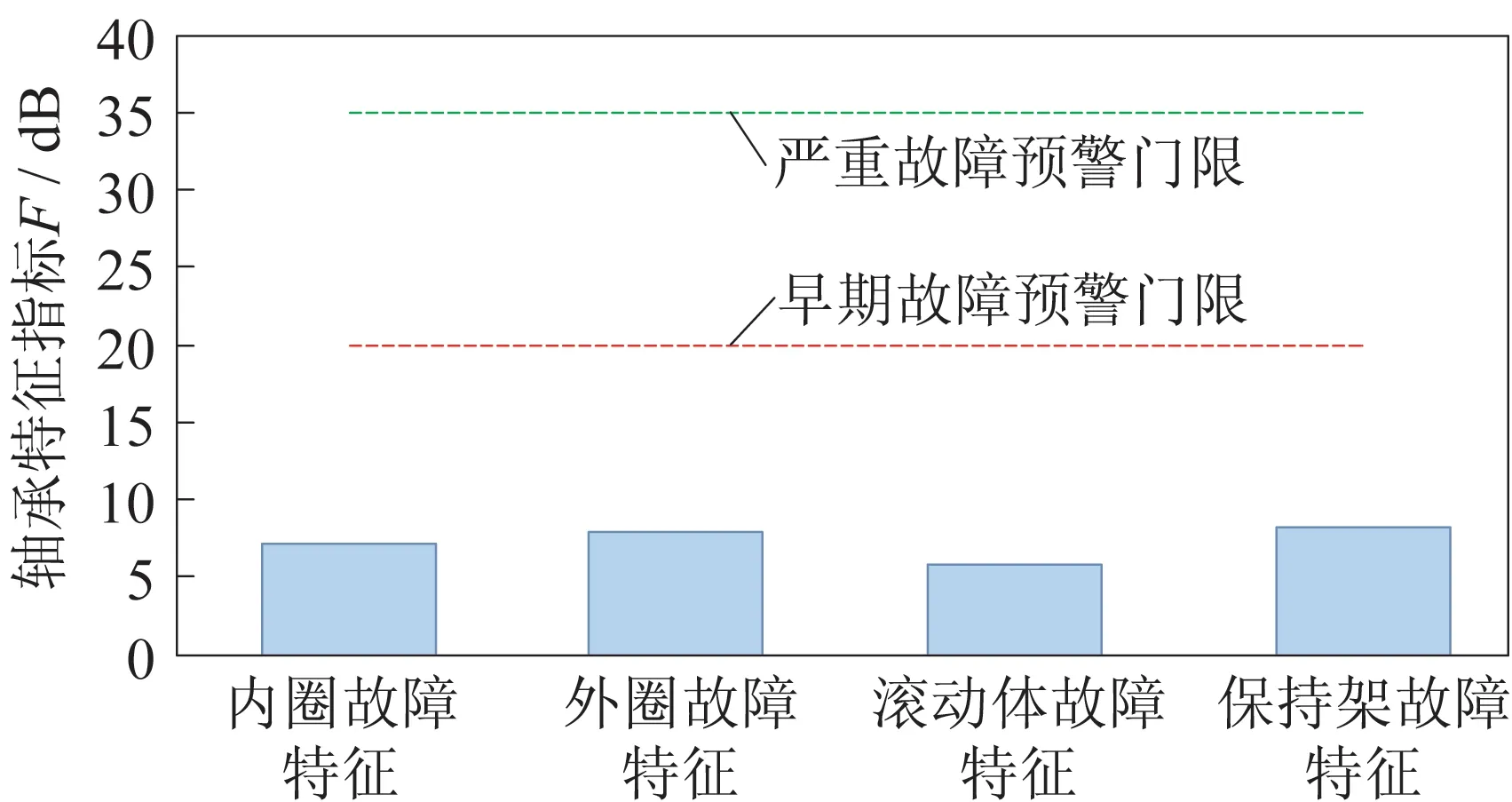
图6 轴承内圈、外圈、滚动体和保持架特征指标Fig.6 Feature indices of the bearing inner-ring，outerring，roller，and cage

5 结束语

针对航天精密伺服机构轴承运行工况复杂、样本数少且缺乏合理评估手段，本文开展基于特征定量识别的精密伺服机构轴承运行可靠性评估应用研究。以自适应标准多小波包解调分析准确提取表征精密伺服机构轴承运行品质的动态特征信息，再以脉冲冲击法对其进行量化识别与评价，采用尾部修正的降半正态分布隶属函数构建轴承运行可靠度模型，将轴承运行状态定量识别结果映射至运行可靠度的归一化区间［0，1］，从而实现航天精密伺服机构轴承的运行可靠性评估。工程实例表明：该方法可以有效揭示试验台轴承外圈损伤所引起的运行可靠性降低，并成功评估某型航天精密伺服机构轴承运行状态。