半刚性T型连接节点有限元分析

孙雨欣 （安徽省建筑科学研究设计院，安徽 合肥 230031）

1 引言

梁柱连接节点是钢框架内力传递过程中的重要部件。多次震害调查均显示，采用栓焊连接的梁柱刚性连接节点在大震下容易出现连接处焊缝撕裂等脆性破坏，导致框架结构丧失承载力[1]。因此，从20世纪末期开始，各国针对半刚性梁柱节点开展了大量研究工作。王燕等[2]提出了半刚性节点初始刚度计算公式，进行了半刚性梁内力分析，并且讨论了半刚性节点对框架内力的影响。石文龙[3]进行了2个平端板半刚性组合节点模拟动力试验，研究了此类节点的工作性能。石永久[4]等通过建立非线性有限元模型，深入探讨了钢框架端板连接半刚性节点的受力性能。宗周红[5]等进行了半刚性连接节点的拟静力试验，探究了此类节点的滞回性能。依照构造形式不同，半刚性节点可以分为T型钢连接节点，外伸端板节点，平齐端板节点，顶底角钢节点和双腹板角钢节点，此类节点均是依靠螺栓进行节点连接。其中T型钢节点采用螺栓连接将钢梁与钢柱或组合结构柱之间通过T型连接件组装而成。研究表明，T型钢连接节点具有较强的节点刚度和良好的变形能力。

虽然国内外学者针对半刚性T型连接节点已有部分研究成果，但由于影响此类节点受力性能的参数较多，因此需要进一步研究此类节点在静力荷载作用下的力学性能。本文采用有限元法对半刚性T型连接节点弯矩-转角关系曲线进行模拟。在验证数值模型准确性后，利用所建立的数值模型针对影响半刚性T型连接节点受力性能的关键参数进行分析，为以后工程结构设计提供有效参考。

2 有限元计算模型

2.1 钢材本构关系

钢材采用二次塑流模型，模型应力-应变关系的数额表达式如下：

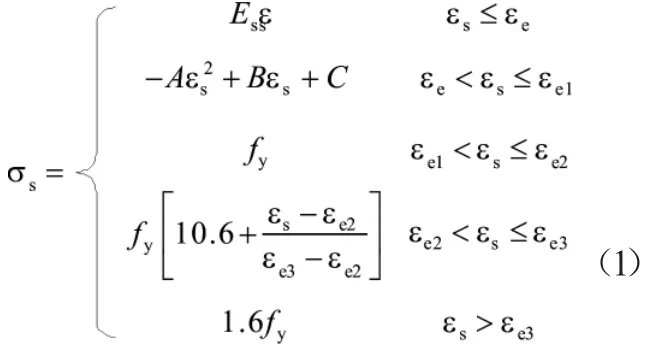
式中εe=0.8fy/Es，εe1=1.5εe，εe2=100εe1，，，；Es为钢材弹性模量；fp、fy、fu分别为钢材的比例极限、屈服极限和抗拉极限强度。如图1（a）所示。

高强螺栓采用双线性随动强化模型，如图1（b）所示。在模型的应力（σ）-应变（ε）关系曲线中，当钢材应力达到屈服应力fy之前，钢材的弹性模量为Es，当钢材应力达到超过屈服应力fy之后材料塑性模量变为0.01Es。钢材弹性模量Es为206000MPa，弹性阶段泊松比ν为0.3。

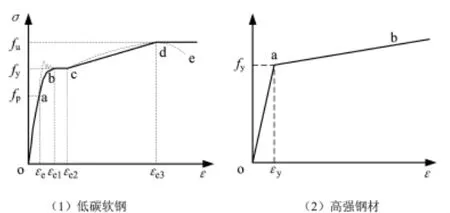
图1 钢材的应力(σ)-应变(ε)关系曲线

2.2 有限元模型

模型采用三维实体单元C3D8R，钢材与钢材之间法向采用硬接触，切向采用罚函数，截面间摩擦系数取为0.25。采用牛顿法进行迭代计算。在模型端部截面型心处建立参考点，对参考点与模型端部截面施加耦合约束。采用模拟柱端加载的方式对节点进行加载，对两侧梁端施加能够产生平动滑移的铰接约束，对节点下部柱端施加无滑移的铰接约束，对节点上部柱端施加竖向荷载和水平位移荷载，有限元模型见图2。

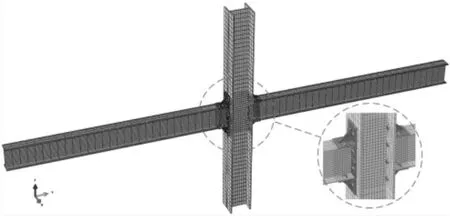
图2 有限元计算模型

2.3 有限元计算结果验证

为了验证有限元模型的准确性，对黄海棠[6]进行的半刚性T型连接节点试验进行模拟，并将计算结果与试验结果进行对比，如图3所示。通过对比可知，本文有限元模型计算结果与试验吻合较好。

图3 有限元计算结果与试验结果对比

3 有限元计算结果及参数分析

为了进一步研究T型钢尺寸、加劲肋厚度、梁柱截面尺寸、柱顶轴压比等因素对半刚性T型连接节点承载能力的影响，建立有限元计算模型，采用柱端加载模式，并对半刚性T型连接节点进行全过程受力分析。有限元模型典型算例基本计算条件：钢柱长度lc=3000mm；一侧钢梁长度lb=3000mm；T型钢长度lt与梁截面等宽；T型钢外伸端设置一道采用三角形加劲肋，加劲肋尺寸-120×120mm，厚度tt=8mm。其余计算参数见表1。其中lc为钢柱长度，lb为钢梁长度，h为截面高度，b1为截面宽度，tw为截面腹板厚度，tf为截面翼缘厚度，n为钢柱轴压比，t1为加劲肋厚度，fy为钢材屈服强度，Nc为节点极限承载力，ke为节点弹性刚度，表中几何尺寸单位为mm，材料强度单位为MPa，承载力单位为kN，结构刚度单位为kN·m。

3.1 有限元计算结果

当半刚性T型连接节点典型算例达到极限承载力时，节点各部分应力云图如图4所示。由图可知，当节点达到极限承载力时，钢梁大部分区域依旧处在弹性阶段，在靠近节点的梁端部受压翼缘出现局部受压屈曲；钢柱节点核心区钢材进入屈服阶段，并且呈45°向梁端受压翼缘方向发展；节点连接部位高强螺栓群均处在弹性阶段，说明该螺栓连接能够满足节点剪力及弯矩传递要求；T型连接件在节点区承担重要传力作用，与钢梁受压翼缘连接的T型连接件加劲板根部出现局部应力集中现象，T型钢板件连接处钢材进入屈服阶段。

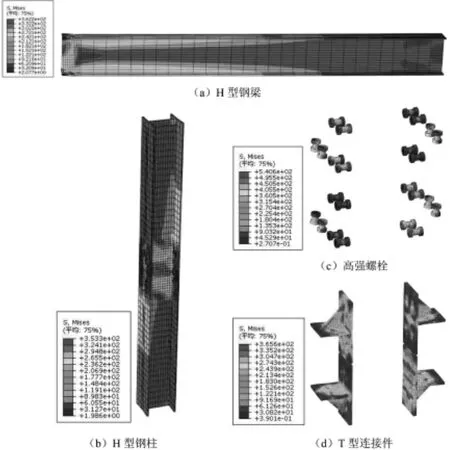
图4 节点应力云图

3.2 参数分析

3.2.1 T型钢尺寸

T型钢外伸长度分别为150mm、200mm和250mm时，半刚性T型连接节点柱顶水平反力（P）-柱顶位移（Δ）关系曲线如图5（a）所示，节点极限承载力和节点弹性刚度见表1。

计算表明，与T型钢外伸长度为150mm的试件相比，外伸长度为200mm和250mm的试件，节点极限承载力分别增大了1.21%和1.87%，节点弹性刚度分别提高了1.20%和1.80%。适当增加T型钢外伸长度能够使节点受力性能略有提高，但影响幅度不大。

3.2.2 加劲肋厚度

半刚性T型节点外伸段设置厚度分别为4mm、8mm的三角形加劲肋以及不设置加劲肋时，半刚性T型连接节点柱顶水平反力（P）-柱顶位移（Δ）关系曲线如图5（b）所示，节点极限承载力和节点弹性刚度见表1。

计算表明，与外伸段设置8mm厚的三角形加劲肋相比，加劲肋厚度为4mm的试件和不设置加劲肋的试件，节点极限承载力分别减小了5.9%和10.9%，节点弹性刚度分别降低了6.0%和11.0%。结果表明，在T型钢外伸段设置适当的加劲肋能够改善此类节点受力性能。

3.2.3 柱截面高度

保持其他几何尺寸不变，分别计算柱截面高度为 250mm、300mm和350mm时试件的受力全过程分析，半刚性T型连接节点柱顶水平反力（P）-柱顶位移（Δ）关系曲线如图 5（c）所示，节点极限承载力和节点弹性刚度见表1。

计算表明，与柱截面高度为300mm的试件相比，柱截面高度为250mm试件的极限承载力减小了11.7%，弹性刚度降低了18.9%；而柱截面高度为350mm试件的极限承载力增大了10.6%，弹性刚度提高了8.2%。结果表明，适当增加柱截面高度能够有效改善此类节点受力性能。

3.2.4 梁截面高度

保持其他几何尺寸不变，分别计算梁截面高度为 250mm、300mm和350mm时试件的受力全过程分析，半刚性T型连接节点柱顶水平反力（P）-柱顶位移（Δ）关系曲线如图 5（d）所示，节点极限承载力和节点弹性刚度见表1。

计算表明，与梁截面高度为300mm的试件相比，梁截面高度为250mm试件的极限承载力减小了14.0%，弹性刚度降低了35.9%；而梁截面高度为350mm试件的极限承载力增大了20%，弹性刚度提高了20.0%。结果表明，适当增加梁截面高度，不但能增大节点极限承载力，也能显著提高节点弹性刚度。

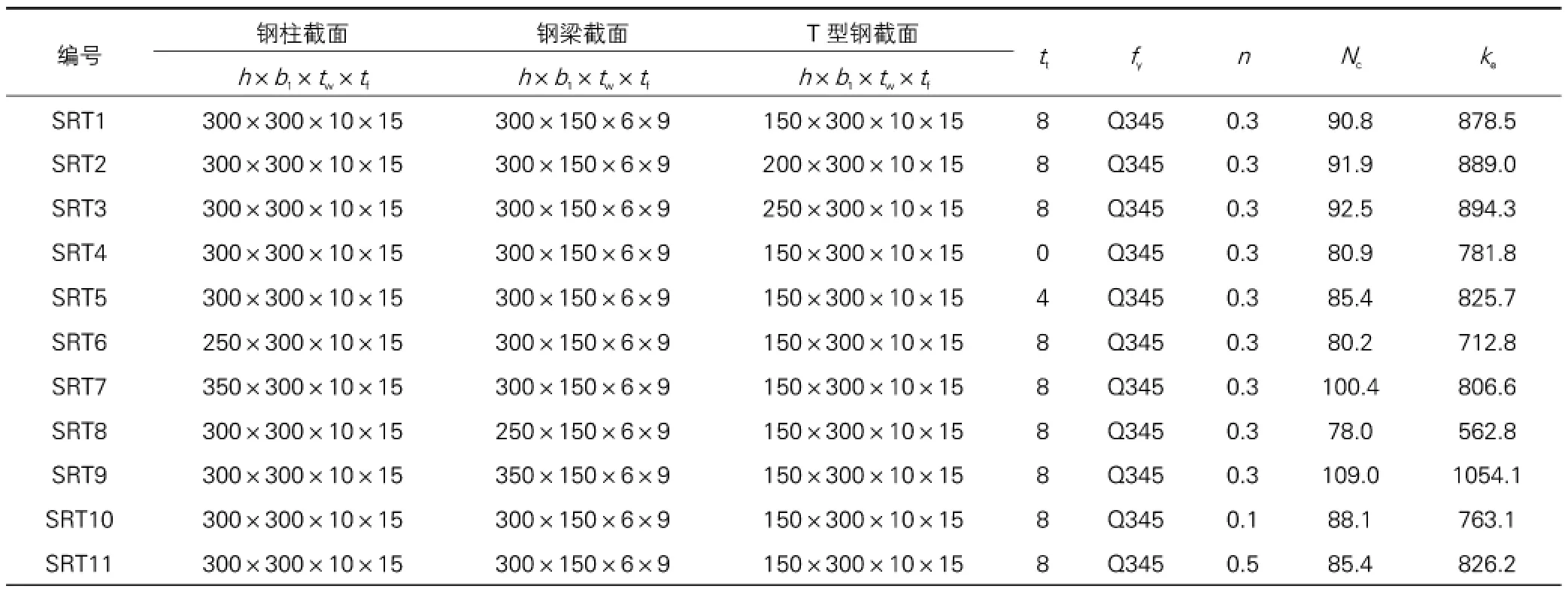
有限元模型计算参数 表1

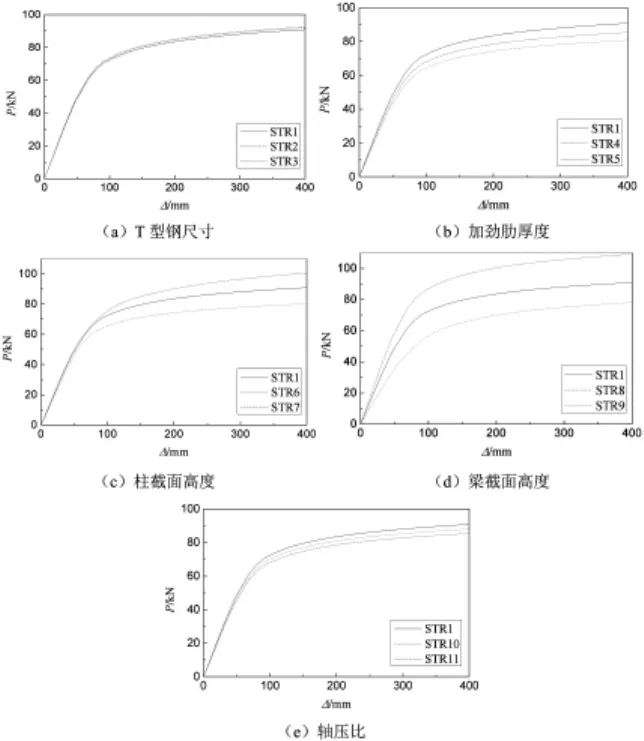
图5 节点柱顶水平反力-柱顶位移关系曲线

3.2.5 柱顶轴压比

保持其他计算条件不变，分别计算柱顶轴压比为0.1、0.3和0.5时试件的受力全过程分析，半刚性T型连接节点柱顶水平反力（P）-柱顶位移（Δ）关系曲线如图5（e）所示，节点极限承载力和节点弹性刚度见表1。

计算表明，与柱顶轴压比为0.3的试件相比，柱顶轴压比为0.1试件的极限承载力减小了3.0%，弹性刚度降低了13.1%；而柱顶轴压比为0.5件的极限承载力减小了5.9%，弹性刚度降低了6.0%。结果表明，当轴压比较小时，随着柱顶轴压比增加，半刚性T型连接节点的极限承载力和弹性刚度均略有增加；而当轴压比较大时，增大轴向荷载会削弱节点受力性能。

4 结论

本文建立了半刚性T型连接节点的有限元计算模型，考虑了连接节点界面接触问题、材料非线性、结构大变形下几何非线性以及加载过程中的边界非线性，在此基础上，将其他文献试验结果与本文所建立有限元模型计算结果进行对比，验证了有限元模型的准确性。采用单调加载的方式，重点研究了此类节点的受力性能。

影响半刚性T型连接节点受力性能的主要因素包括加劲肋厚度、梁柱截面尺寸、柱顶轴压比等，其中增大梁柱截面高度不但能提高节点极限承载力，也能显著提高节点弹性刚度。而在有限范围内修改T型钢外伸长度对节点受力性能没有明显影响。