探究本质 追根溯源 延展应用 提升素养——以一道质检试题为例

广东 闫 伟

直线与抛物线交汇问题是高考和模考中的重点考查对象，其内涵丰富，灵活多变，具有较高的研究价值.本文对武汉市2020届高中毕业生质量检测试题中的第19题进行深入研究，探究试题本质，并对结论进行拓展及延伸应用，以此指导高三复习备考，实现高效复习.

1. 试题呈现与分析

(1)求抛物线Γ的方程；

(2)已知经过点A(3,-2)的直线交抛物线Γ于M,N两点，经过定点B(3,-6)和M点的直线与抛物线Γ交于另一点L，问直线NL是否恒过定点，如果过定点，求出该定点，否则说明理由.

试题分析：试题表面常规、内涵深刻，给人以“题在书外，根在书内”的感觉，从知识层面看主要考查抛物线的标准方程、几何性质、直线和抛物线的位置关系及直线过定点问题，均是解析几何中的热点和难点；从能力层面看主要考查学生运算求解、推理论证等能力，试题较好地检测了学生的数学素养和学习潜能.

2. 解法探究

(1) 抛物线Γ的方程为y2=4x，过程略；

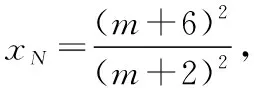
评注：本解法通过设M点坐标表示直线MA,ML的方程，进而与抛物线方程联立得N,L两点坐标，并求得直线NL的方程，从而得到定点坐标，解题思路清晰明了，但是运算极其繁杂，对学生的运算能力要求较高.

评注：本解法相对于解法1，运算量就小很多，通过求设M,N,L坐标并表示出直线MN，ML的方程，结合已知点A,B坐标求得N,L两点纵坐标之积，这是突破本题的关键，虽说变量较多，只要牢牢把握N,L两点坐标这一本质就不难得到结果，学生应重视相关结论的积累.

3 .基于GeoGebra的探究及反思

通过以上的分析和解答，得知直线NL恒过定点(-3,0)，那么该定点和题目中的抛物线参数p以及点A,B的坐标有关系吗？如果将参数p以及点A,B的坐标一般化，定点又会是什么呢？由于涉及的运算和直线NL的直线方程较为复杂，探寻定点有一定的难度，因此笔者借助于GeoGebra平台进行探究，通过实验演示找到与上述参数相关的定点，同时为后面的代数证明提供更加直观形象的思路支持.

图1

图2

通过实验探究可知：只有当A,B两点的纵坐标乘积等于参数p与横坐标m的乘积的2倍，即ns=2pm时，直线NL恒过定点(-m,0). 于是我们可以将试题结论一般化.

4. 推广结论，揭示本质

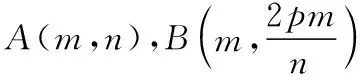
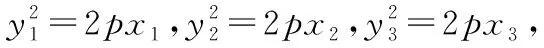
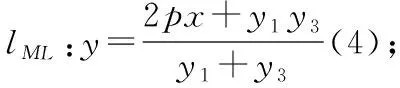
通过以上证明可知，试题条件中的A,B点似乎有些多余，因为直线NL恒过的定点(-m,0)仅仅和N,L两点的纵坐标之积以及参数p相关，即yNyL=2pm；于是上述结论可以继续优化.

结论2：已知抛物线Γ:y2=2px(p>0)，N(x1,y1),L(x2,y2)是抛物线上异于原点的两个点，若满足y1y2=2pm，则直线NL恒过定点(-m,0).

结论2的证明过程与结论1一样，此处不再赘述. 由结论2可知，要想解决试题中直线NL过定点问题必须先要求解N,L两点纵坐标的积，这才是试题的本质；相对于试题中先给出两个定点A,B，再过A,B的直线与抛物线相交产生M,N,L三点，条件繁冗，干扰性较大，很多学生对于条件中诸多参变量之间的转化关系较陌生，其根源在于没有把握好试题的本质，对于隐藏在题目背后的意图没有理解到位，这就需要学生在平时重视常用结论和方法的积累，善于钻研和思考问题的本质规律，从而提高复习备考效率.

我们在探究一个问题时应该从多角度分析，充分挖掘其潜在的价值，现对结论2进行逆向探究可以得到：

结论3：已知抛物线Γ:y2=2px(p>0)，若过点M(m,0)的直线交抛物线于N(x1,y1),L(x2,y2)两点，则有y1y2=-2pm，且x1x2=m2.

5. 追根溯源，总结提升

苏教版普通高中课程标准实验教科书《数学(选修2-1)》第54页习题2.4第12题如下：

设过抛物线y2=2px的焦点的一条直线和抛物线有两个交点，且两个交点的纵坐标为y1,y2，求证：y1y2=-p2.

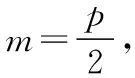
本题实质是上述质检试题的源头，茫茫题海，问解何处觅，课本寻根、课本探源.因此在平时的教学过程中，要学会对问题的深入探究以及对同根同源同宗问题的延续及推理.

直线与抛物线、椭圆的位置关系一直是高考和模拟考中的热点和难点，在很多圆锥曲线题目中都是探求一些特殊结论(如定点、定值问题)，这些结论看似特殊，实则都具有普遍性，它们的背景往往是某种圆锥曲线的一个特定性质，由这些性质可以衍生出许多形式不同但本质相同的试题，研究这类试题不仅能够更好地把握解析几何的本质，还能扩展视野、提升解题能力以及核心素养.在平时的学习过程中，不仅要学会推理，寻找联系，还要学会对一些结论进行整理、推广及应用.

6. 延展应用，拾级而上

上述结论虽说不难求证，但是若能合理地运用在解决一些直线与抛物线相交的问题上，则可以减少大量的运算过程，避免繁冗的推理，实现高效解题，下面举例说明.

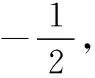
评注：本题的解题关键在于由斜率结果转化到A，B两点纵坐标的乘积为定值，再结合上述结论2锁定直线AB恒过的定点，从而可知当直线AB与定点和原点的连线垂直时，距离最大；借助结论我们可以迅速找到问题的突破口，抓住本质，有效地降低了试题难度.

【例2】若抛物线C:y2=4x的焦点为F，过点P(2,0)的直线交抛物线于A(x1,y1),B(x2,y2)两点，直线AF,BF与抛物线交于M,N两点.

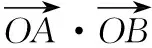
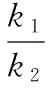
评注：由于直线AM,BN都过焦点，解题的关键在于借助结论3将M,N坐标关系转化为A,B的坐标关系，从而得到两直线斜率的等量关系式；在解题时合理使用结论能简化推理和运算过程，具有简洁、直观的特点，极大地提高了解题效率.

7. 结束语

高考和模拟考中的试题大部分都是源于课本但又高于课本，结论虽然陌生，但又有据可依.因此在平时的课堂教学中，要多把教材上的知识点、例题以及练习题作为学习的第一资源，多加探究、联想、类比、拓展,串联一些相关的知识,让考试回归课本，让解决问题变成水到渠成的事情，这样我们的数学课堂才会更高效.