基于小波-高阶矩模型的投资组合策略
——以国际原油市场为例
2020-11-21朱鹏飞
朱鹏飞,唐 勇,钟 莉
(1. 福州大学经济与管理学院,福建 福州 350116;2. 金融数学福建省高校重点实验室(莆田学院),福建 莆田 351100;3. 福建省金融科技创新重点实验室,福建 福州 350116)
1 引言
石油作为当今世界上最重要的能源之一,已经渗透到各个工业部门,在国民经济发展过程中扮演不可替代的角色,被称为“工业之血”[1-2]。作为最大发展中国家的中国,近年来对于石油的需求与日俱增,2013年9月超越美国,成为世界上最大的原油进口国家,同时中国石油对外依存度也提升到了61.7%,引起了社会各界的关注[3]。
国际原油价格的波动将会影响一国经济的发展,社会的稳定以及民众的福祉[4],但是由于全球政治经济形势的不明朗以及诸多因素的影响,导致国际原油价格波动剧烈,暴涨暴跌现象屡见不鲜。早在2003年到2008年期间,受益于新兴经济体的蓬勃发展,国际原油价格一直处于上涨通道,纽约油价一度创下了每桶147.27美元的历史最高价。但是随后受美国次贷危机的冲击,纽约油价一泻千里,跌幅高达75%。在经历了数年牛市后,脆弱的供需平衡再次被打破,2014年10月国际原油价格“历史重现”,纽约油价跌幅甚至达到67%。大量的已有研究表明,构建跨市场的投资组合能有效的减少乃至规避风险,为投资者带来稳定的收益[5]。因此,在国际油价变动剧烈的背景下,构建跨多个原油市场的投资组合将会具有一定的理论与现实意义。
由Markowitz提出的均值-方差模型(Mean-Variance,M-V)[6]奠定了现代投资组合理论的框架,并得到不断的改善[7-8]。《巴塞尔协议》将VaR作为风险度量的工具,使得传统投资组合研究转化为如何实现VaR最小化问题[9-10],但是均值-VaR投资组合模型存在非一致性的缺陷[11],而CVaR的使用恰好解决此问题。Krokhmal等[11]对均值-VaR和均值-CVaR投资组合模型的优劣进行了比较,证明了均值-CVaR模型的优势性。张翼等[12]实证结果证明了均值-CVaR模型纳入Copula函数后,能够更为有效且准确地预测投资组合的CVaR。Liu等[13]构建GARCH-Copula-CVaR投资组合模型,结果表明该方案的效果明显优于对照组,在降低组合风险同时提升了组合的收益。
在传统的均值-方差投资组合框架中,金融资产的回报和风险分别以其均值来和方差来描述。该模型成立的假设条件是投资者具有二次效用函数或收益服从正态分布,然而这两种情况实际上却难以存在,同时大量的实证结果已表明收益率序列往往表现出尖峰肥尾特征[14]。虽然VaR和CVaR隐含了一些高阶矩信息,能够在一定程度上反映收益的尖峰肥尾分布[15],但不同风险偏好投资者对于高阶矩风险偏好不同,例如非绝对厌恶风险的投资者往往偏好收益率右偏分布以及较低的峰度[16],这些都是传统均值-VaR和均值-CVaR投资组合模型难以满足的。一些学者将高阶矩估计引入到均值-方差模型中,扩展为均值-方差-偏度-峰度模型(Mean-Variance- Skewness- Kurtosis, M-V-S-K),该模型通过放松收益率服从正态分布的假设扩展了其适用性和有效性,例如:蒋翠侠等[17]考虑到高阶矩风险的时变特征,构建高阶矩动态组合投资模型,从理论和实证两个方面证实高阶矩模型的有效性和可行性。Martellini和Ziemann[18]引入高阶矩思想到协方差矩阵和余弦参数的估计过程中,结果表明使用新的包含高阶矩估计产生的投资组合将会明显改善投资者的福利。Nguyen[19]提出了一种新的模糊集合投资组合选择模型,利用资产的边际效应对投资组合的高阶矩进行模糊多目标线性规划,实证结果表明该方法较以前的投资组合模型更为有效。Chen Wei等[20]基于不确定性理论,在考虑投资者对于不同阶矩风险偏好的基础上,提出了一种不确定多目标投资组合优化模型,并用花朵授粉算法进行求解,实证结果表明其可行性和优势性。
金融市场投资者往往具有异质特征,金融市场在同一时期交易是由不同频率(周期)构成,由此产生的金融时间序列兼有时域和频域双重特征,采用单一时域模型并不能准确刻画金融时间序列间的相依结构[21-22]。以上的投资组合模型恰恰忽略了多时间尺度的价值,并不能刻画频域上的复杂特征,实际上也难以满足投资者多样化的实际需求。小波理论被称为“数学显微镜”,其优势在于可以根据异质性时间层次对市场划分,在时频分辨率上分解时间序列,充分挖掘多时间尺度的丰富信息。然而诸如Wang Gangjin等[23]、Jena等[24]以及王莹[25]基于小波视角,虽然研究方法、内容及对象不同,但都只是对金融市场复杂机理和特征进行检验和分析,并没有同投资组合、套期保值等金融实践活动形成有效衔接,制约了小波理论的应用范畴。
鉴于此,本文的创新点和主要贡献在于:(1)将极大重叠离散小波变换研究方法引入到高阶矩投资组合框架中,提出小波-高阶矩投资组合模型。该框架一方面能够处理具有不连续、非平稳、尖峰肥尾等复杂特征的金融时间序列。另外一方面针对金融时间序列兼有时-频域双重特征,其能够充分利用多时间尺度价值,挖掘高频部分和低频部分的各阶矩特征,为不同交易周期投资者提供差异化的投资组合方案。(2)借鉴Zhang等[26]、Li Fangfang等[27]基于EMD方法提出的“分解-预测-集成”思想,本文将分解后各个时间尺度上的高阶矩投资组合进行重构,得到频域视角下的高频尺度集成方案和时-频域视角下的全尺度集成方案,该重构方案充分挖掘和利用高频部分和低频部分的信息,兼顾不同交易周期的需求,将会为投资者提供更优的资产配置策略。(3)考虑到投资者除了异质性特征外,还具有不同的风险偏好特征[20]。本文将这些风险特征纳入到小波-高阶矩投资组合模型中,通过对比国际原油投资者97种不同风险特征在各个时间尺度上的投资效果,遴选出恰当风险偏好特征来构建更高效的资产配置方案,并经过不同市场环境的稳健性检验,证明其可靠性。以上这些研究内容都是以往文献鲜有涉及到的。
2 研究方法
2.1 极大重叠离散小波变换方法
极大重叠离散小波变换方法(Maximal Overlap Discrete Wavelet Transform,MODWT)凭借着适合任何样本容量、平移不变性等优势,已得到广泛地使用[28-30]。参照文献[28-30],鉴于LA(Daubechies Least Asymmetric)小波函数的优势,本文在此采用滤波器宽度为8的LA小波函数。MODWT方法具体步骤如下:

(1)
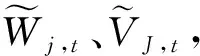
(2)
便可以得到J个向量小波系数和一个向量尺度系数分别为:
(3)
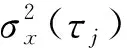
(4)

时间序列{xt}和{yt}在尺度τj=2j-1上小波协方差定义为[31]:
(5)
根据文献[31],定义小波偏度S(τj)和峰度k(τj)如下:
(6)
(7)
依据此,也可以推断出对应的协偏度和协峰度公式,例如
x、y分别代表不同变量,sxyy(τj)、kxyyy(τj)、kxxyy(τj)以此类推。
2.2 小波-高阶矩投资组合模型构建
大量文献表明在市场呈现过度峰态和肥尾特征时,高阶矩风险度量更为重要[16]。鉴于此,一些学者将均值-方差模型(Mean-Variance, M-V)扩展为均值-方差-偏度-峰度模型(Mean-Variance- Skewness- Kurtosis, M-V-S-K)[17-20],其谋求实现均值和偏度最大、方差和峰度最小的四目标,具体模型详见公式(8)如下[16]:
(8)
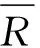
鉴于金融市场存在时域和频域双重特征,以上的四阶投资组合模型无法利用多时间尺度的丰富信息,并不能刻画频域上的复杂特征,实际上难以符合不同交易周期和交易频率的投资者差异化需求。鉴于此,本文将极大重叠离散小波变换方法与均值-方差-偏度-峰度模型结合,提出了小波-四阶矩投资组合模型,如下:
j=1,2…J
(9)

(10)

参考文献[16-17],本文采用多项式目标规划方法(Polynomial Goal Programming,PGP)对公式(9)进行求解。PGP方法是将公式(9)各种目标拆分成四个单目标,接着再将四个单目标合并成一个单目标函数。具体来看:
首先计算各个单目标最优水平,Rj(X)*、Vj(X)*、Sj(X)*、Kj(X)*分别代表在不考虑其他目标情况下单目标最优值,计算步骤详见公式(11)~(14),其中j=1,2…J,如下:
(11)
(12)
(13)
(14)

j=1,2…J
(15)

2.3 集成小波-高阶矩投资组合方案
根据Maharaj[32]的研究,金融时间序列之间的矩风险联动对时间尺度是敏感的,反映出各个频率(周期)投资者的行为特征。Zhang等[26]、Li Fangfang等[27]等基于EMD方法提出了“分解-预测-集成”思想,他们认为模型的综合集成可以最大限度地利用各个模型优势,采用更多的预测信息,是提高预测性能的有效方法。本文借鉴该思想,在小波-高阶矩投资组合模型基础上,分别提出高频尺度集成方案和全尺度集成方案,最大限度的利用各个时间尺度的优点,采用丰富的多时间尺度价值,考虑不同交易周期行为特征。

(16)
其中xij代表第i种资产基于小波-高阶矩投资组合模型在j层上的权重,根据公式(15)可得,gxi则代表第i种资产的高频尺度集成部分的权重。gxi基于频域视角,最大限度的利用高频部分各个时间尺度丰富的细节信息,综合反映了短期和中期的趋势变动。
长期时间尺度(低频部分)表征的是时间序列的总体趋势,对应极大重叠离散小波变换低频部分,虽然信号变换最为粗糙,但是却能基于时域视角刻画和提取金融信号的基本特征[38],基于此,构建以下的全尺度集成方案:
(17)
其中xij定义如上,XiJ代表第i资产基于小波-高阶矩投资组合模型在长期尺度上的权重,根据公式(15)可得,qxi则代表第i种资产的全尺度集成部分的权重。qxi基于时-频域双重视角,最大限度的利用高频部分的细节信息和低频部分的的基本特征,综合反映了短、中、长期的趋势变动。
3 实证分析
3.1 数据描述与处理
美国西德克萨斯轻质原油(简称为WTI)、英国北海布伦特轻质低硫原油(简称为Brent)、迪拜酸性原油(简称为Dubai)并称为国际原油价格三大指数[3]。在此选择WTI原油现货指数、Brent原油现货指数、Dubai原油现货指数的日价格数据作为研究对象,前两者数据来源于EIA(美国能源信息署),后者数据来源于凤凰财经网。总样本数据区间从2006年10月11日到2018年5月16日,删除非共同交易日,各包含2800个交易日,指数均以美元计价。
对三个原油指数采用对数差分处理,得到各自的收益率序列,基于Eviews8.0软件对收益率序列进行统计描述,详见表1。表1显示,三个序列“尖峰肥尾”特征表现显著,并不服从正态分布。同时,Q统计量在滞后20和30阶时,均自相关特征显著。ADF单位根检验结论表明序列均是平稳的。

表1 统计性描述
3.2 样本外检验结果分析
评价一个模型的效果如何,关键取决于样本外预测效果[33]。因此,本文基于滚动窗口方式,进行样本外预测检验和分析,具体来看:以2006年10月11日到2015年10月12日区间即约9年共计2171个数据为第一次估计样本区间,对2015年10月13日最优投资组合权重进行预测,并以此为依据构建投资组合。以此类推,以第i个交易日前2171个交易日作为滚动窗口区间(窗口长度固定为2171),基于此来对第d1个交易日的最优投资组合权重进行预测,持续滚动向前一步预测,共进行629次模型估计,获取样本外629个交易日的最优投资组合权重配置方案。
利用上述的滚动窗口技术,基于本文提出的小波-高阶矩投资组合模型,暂设不考虑投资者风险偏好即假设{λj}={1,1,1,1},根据公式(15)进行各个时间尺度的样本外预测,满足原油市场投资者不同交易周期的实际需求。接着根据公式(16)~(17),构建高频集成和全尺度集成两个资产配置方案,分别从频域视角和时-频域视角进行集成预测。参考文献[34-35]并根据估计样本区间长度,选择最大分解层数J=4即4层高频部分和1层低频部分。以下分别用d1~d4表示高频部分,a4表示低频部分,各个时间尺度含义见表2,如下:

表2 小波时间尺度含义
在此选择单一市场、等权重、M-V-S-K、M-V-S、M-V-K、M-V、Mean-CVaR(90%、95%、99%)、Mean-VaR(90%、95%、99%)14组策略作为对照组进行比较。M-V-S-K、M-V-S、M-V-K、M-V模型建模过程详见文献[16],Mean-CVaR和Mean-VaR模型建模过程详见文献[11],在此不再赘述。全文均采用MATLAB2016a软件进行模型估计和运算。参考以往文献[13]、[17]、[36]做法,选用日均收益率、波动、夏普比率及效用作为评价指标,见表3和表4,如下:

表3 对照组样本外检验结果

表4 小波-高阶矩投资组合模型样本外检验结果
由表3~4可知,与传统对照组相比,小波-高阶矩投资组合策略在绝大部分尺度上表现较好,具体分析如下:
(1)从收益率角度来看,除了长期尺度a4外,高频部分和集成部分的小波-高阶矩投资组合模型均优于所有对照组,这说明较传统模型而言,本文提出的小波-高阶矩投资组合模型能为不同交易周期投资者提供更高的收益。
(2)从波动角度来看,大部分的小波-高阶矩策略依然能够同时优于全部对照组,具有良好的避险能力。但是短中期尺度d1、d2、d3表现较差,未能取得良好的降低风险效果。该现象出现的原因可能与样本外区间范围内市场经历了暴涨暴跌有关,短期极端信息不断冲击投资者的脆弱心理,诱发的“动物精神”[37]将会驱使投资者做出不理智行为,尤其是在短中期交易行为上表现最为明显。
(3)从夏普比率来看,除了低频部分a4外,高频部分和集成部分的小波-高阶矩投资组合模型均同时优于14组对照组。同时,在投资组合模型内部各个部分的表现也存在差异,中期时间尺度d4、高频尺度集成及全尺度集成表现最佳,而长期时间尺度a4表现最差。
(4)从效用来看,投资者在大部分时间尺度上均能从本文提出的小波-高阶矩策略中获得较高的效用,满足投资者多样化的需求,再次验证本文提出的小波-高阶矩模型的优势。
综上所述,无论是何种指标,大部分的小波-高阶矩投资组合策略均能同时优于14组对照组,为不同交易周期的投资者在波谲云诡的原油市场上取得更佳的组合效果,这表明本文提出的小波-高阶矩投资组合模型的有效性和优势性。
同时,小波-高阶矩投资组合模型内部存在明显的差异:中期尺度d4虽然在各个方面表现最佳,但是由于中期尺度d3在风险规避方面的不足,使得中期尺度总体表现并不稳定,稍逊于集成部分。短期尺度次之,而长期尺度a4表现最差。与之形成鲜明对比,集成部分的两个策略综合利用各个时间尺度的丰富信息,表现最为稳定,其中高频尺度集成侧重于谋求更高收益,而全尺度集成侧重于降低组合波动,此结果说明本文构建的高频尺度集成方案和全尺度集成方案将会为投资者提供更加稳健的投资组合结果,证明其可行性和有效性。
3.3 不同风险偏好的样本外检验结果分析
在投资过程中,投资者除了异质性外,还具有不同的风险偏好特征,这些偏好往往会影响投资策略[16-17]。那么在不同时间尺度上,不同风险偏好是否会影响小波-高阶矩投资组合的效果呢?哪种风险偏好配置将会优化各个时间尺度上的资产配置呢?鉴于此,本文依托小波-高阶矩投资组合模型,以时-频域双重视角探究原油市场投资过程中风险偏好对不同时间尺度上的影响,谋求能改善组合效果的风险偏好配置。
在小波-高阶矩投资组合模型中,λj代表的是投资者对于第j阶矩风险的偏好程度,λj越大表示投资者对第j阶矩风险越偏好,参考文献[16-17],假设λj范围为0~3:λj=0代表对第j阶矩风险无偏好,λj=1代表对第j阶矩风险存在偏好,λj=2代表对第j阶矩风险有明显偏好,λj=3代表对第j阶矩风险最为偏好。
为了使得构建的{λj}符合实际情况且能最全面代表不同时间尺度上投资者的风险偏好特征,对{λj}施加以下条件约束:(1)在{λj}(j=1,2,3,4)中,至少有1个λj=3且最多有2个λj=3。(2)在{λj}(j=1,2,3,4)中,至少有1个λj=1。(3)至多有1个λj=0。设置以上约束条件是为了构建投资者对不同阶矩风险有区别的偏好,基于此约束条件,共构建94组不同的风险偏好配置。此外,也考虑{λj}={1,1,0,0}、{1,1,1,0}、{1,1,0,1}这三种情况。综上所述,共对97种风险偏好配置进行小波-高阶矩投资组合模型样本外检验和分析。
利用上述的滚动窗口技术,根据公式(15)进行各个时间尺度的样本外预测,接着根据公式(16)~(17),构建高频尺度集成和全尺度集成两个资产配置方案,检验结果如下:
经过实证检验,在97组风险偏好配置中仅有28组能够比原始模型取得更优的投资组合效果,其他大部分风险偏好特征最终的效果实际上将会对投资者的账户造成负面影响。根据表5,在表现最佳前7组风险偏好配置组合中,大部分对于三阶偏度风险或四阶峰度风险给予3的最大偏好,这说明对于高阶矩风险的重视将会为投资者带来更优的资产配置方案。

表5 优于原始模型的部分风险偏好组合
根据表6,{λj}={2,1,2,3}的风险偏好配置侧重于防范峰度风险,兼顾偏度和收益,也对方差有一定的偏好,最终取得了良好的投资组合效果,最为明显改良了原始小波-高阶矩投资组合模型。对绝大部分的高频部分、低频部分以及集成部分而言,投资组合的盈利能力得到提升,夏普比率得到明显改善,效用得到加强。在样本外区间内,市场经历了一轮暴跌和暴涨,表现出明显的尖峰肥尾特征,正如Maringe和Parpas[14]所言,在数据被扭曲即市场表现出过度偏度和峰态时,高阶矩风险尤为重要,{λj}={2,1,2,3}则恰恰契合了市场实际运行规律和特征,为投资者带来更佳的组合效果。

表6 表现最佳的风险偏好配置检验结果
此外,从表6还可知,该风险偏好配置并非对所有的时间尺度都有效,该偏好明显改善了集成部分和短中期时间尺度d1、d2、d3的投资效果,却并没有改善中期尺度d4,而长期尺度a4虽然在三个指标上得到改善,但是实际投资效果依然不及其他尺度,表现较差。该现象出现可能与过于注重峰度风险即关注于短期极端事件[18-19]有关。与此不同,本文提出的高频尺度集成和全尺度集成策略能综合利用各个时间尺度的丰富信息,考虑不同交易周期投资行为特征,在{λj}={2,1,2,3}风险偏好配置下,集成部分的两个策略在四个指标上均得到了改善,并且实际的投资效果较好,在均衡性和稳定性方面优于其他时间尺度。此外,实证结果也验证了前文高频尺度集成侧重于谋求更高收益,而全尺度集成侧重于降低组合波动的结论。
3.4 稳定性检验
本文所提出的小波-高阶矩投资组合模型在不同市场状态中,尤其是原油市场处于极端波动时,能否具有普适性和稳定有效性呢?鉴于此,依据WTI原油价格走势,对总样本区间进行划分:将2006年10月11号~2008年12月23号作为第一个牛熊周期区间;将2008年12月24号~2016年2月11号作为第二个牛熊周期区间;2016年原油市场引来新一轮的暴涨。因此,将2016年2月12号~2018年5月16号作为上涨阶段。接着进行三个区间样本内外划分。具体划分详见图1和表7,如下:
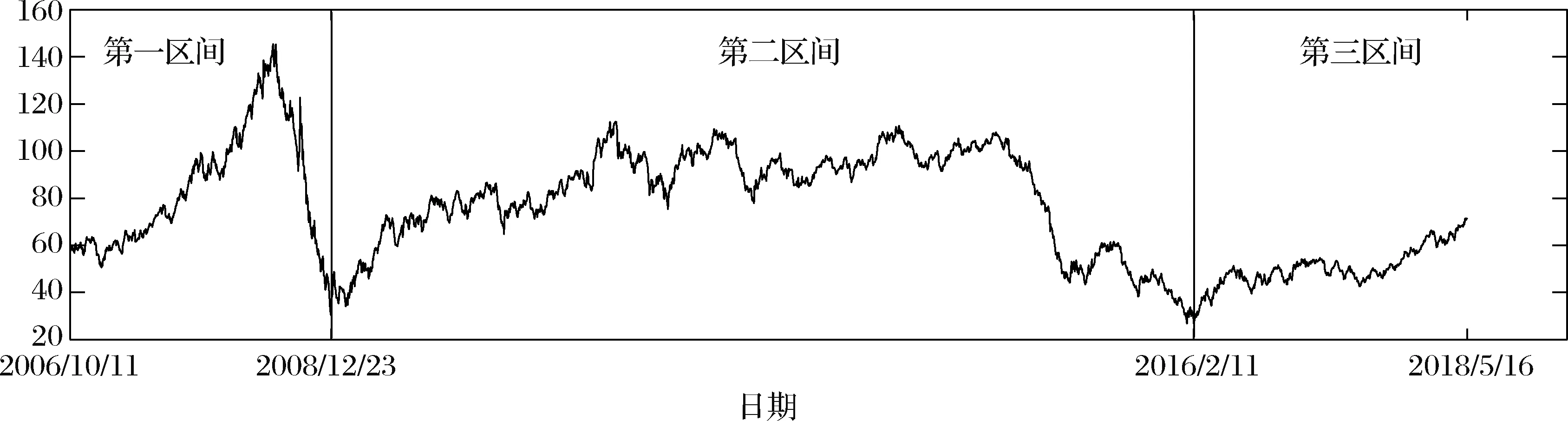
图1 WTI原油现货指数区间划分图

表7 区间划分
利用上述的滚动窗口技术,基于本文提出的小波-高阶矩投资组合模型,首先暂设不考虑投资者风险偏好即{λj}={1,1,1,1},根据公式(15)进行各个时间尺度的样本外预测,满足原油市场投资者不同交易周期的实际需求。然后根据公式(16)~(17),构建高频集成和全尺度集成两个资产配置方案,分别从频域和时-频域视角进行集成预测。接着以时-频域双重视角探究原油市场投资过程中风险偏好在不同时间尺度上的影响,谋求能最大程度改善组合效果的风险偏好配置。三个区间的最终检验结论基本一致,由于文章篇幅限制,本文仅呈现某区间的检验结果。第二区间牛熊周期持续时间最久,并且直接导致了俄罗斯的卢布危机,对世界政治经济格局产生重大影响,故本文在此选择呈现该区间的检验结果。
首先是在不考虑风险偏好特征即{λj}={1,1,1,1}的检验结果,对照组和参考指标与前文一致,样本外检验结果详见表8和表9,如下:
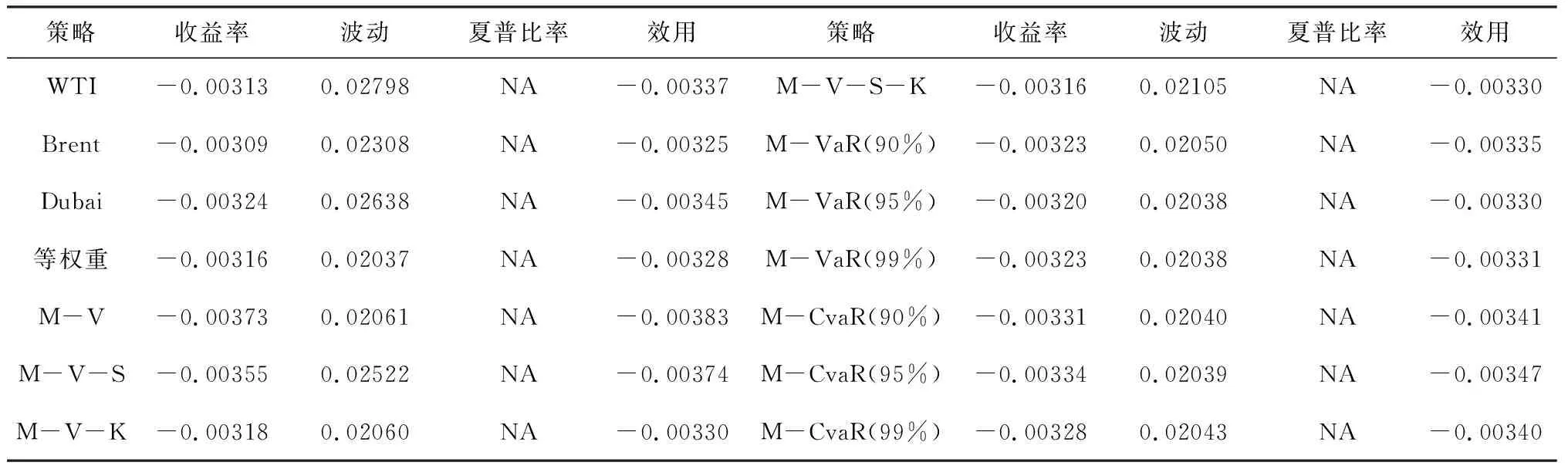
表8 对照组样本外检验结果

表9 小波-高阶矩投资组合模型样本外检验结果
由表8-9可知,相对于对照组而言,小波-高阶矩投资策略取得了更好的投资效果。同时,小波-高阶矩投资组合内部各个尺度差异明显,长期部分和集成部分表现最佳,中期尺度次之,而短期尺度表现最差。与前文不同,此处的长期尺度a4表现最佳,此现象可能与暴跌的市场环境有关:当市场处于极端情况时,注重长期趋势变动的尺度较其他而言更不容易受到短期信息冲击,从而避免了非理性行为的出现。此外,集成部分的两个策略依然表现稳定,高频集成方案侧重于提升收益,而全尺度集成方案侧重于降低波动。
此后对97种风险偏好配置进行小波-高阶矩投资组合模型样本外检验和分析,检验结果详见表10和表11,如下:

表10 优于原始模型的部分风险偏好组合

表11 表现最佳的风险偏好配置检验结果
根据表10,在表现最佳前7组风险偏好配置组合中,大部分对于三阶偏度风险和四阶峰度风险给予3的最大偏好,这说明对于高阶矩风险的重视将会为投资者带来更优的资产配置方案。
根据表11,{λj}={2,1,2,3}的风险偏好配置明显改良了原始小波-高阶矩投资组合模型,稳健性检验与前文基本一致。
4 结语
针对以往研究的不足,本文将极大重叠离散小波研究变换方法与高阶矩投资组合理论框架相结合,提出小波-高阶矩投资组合模型,并基于此构建国际原油投资组合策略。同时,将分解后各个时间尺度上的高阶矩投资组合进行重构,构建基于频域视角的高频尺度集成方案和基于时-频域视角的全尺度集成方案。此外,考虑到投资者具有不同的风险偏好特征,通过对比投资者不同风险偏好特征在各个时间尺度上的投资效果,遴选出恰当风险偏好特征来构建更高效的资产配置方案。最后在不同市场环境中进行稳定性检验。
样本外检验结论如下:(1)相较于14组对照组而言,大部分的小波-高阶矩投资组合模型在为投资者谋求更高收益同时,普遍降低了风险,提升了夏普比率并带来更高的效用。同时,小波-高阶矩模型内部存在明显差异,集成部分表现最为稳定且各项指标均优于14组对照组,中期时间尺度表现较好,短期时间尺度次之,长期时间尺度a4表现最差。(2)只有少部分的风险偏好配置可以优于原始小波-高阶矩投资组合模型,该部分风险偏好特征大部分给予三阶矩偏度或者四阶矩峰度风险3的最大偏好。通过选择合适的风险偏好特征,将会对绝大部分的高频部分、低频部分和集成部分起到改进作用。(3)为了检验本文提出的小波-高阶矩投资组合模型的稳健性和有效性,本文将总样本区间根据牛熊周期进行划分,实证结果表明本文提出的小波-高阶矩投资组合模型无论在牛市还是熊市环境中均能取得优于14组对照组的投资组合效果。并且,部分风险偏好特征能够明显改善小波-高阶矩投资组合模型,取得更佳的样本外预测结果。此外集成部分的两个方案表现最稳定且行之有效,高频集成方案侧重于提升收益,而全尺度集成方案侧重于降低波动。
