基于弹性网—自回归模型的股票价格研究

韩 情 汪子琦 耿文静

(安徽大学经济学院 安徽 合肥 230601)

一、引言

近年来股票投资逐渐成为热门，如何有效提高投资收益成为了学界和业界需要持续探讨和研究的问题。在研究股票价格的众多模型中，时间序列模型最受大家青睐，因为时间序列预测法正迎合股票价格变化发展的随机性及其时变性等特点，可通过建立模型以预测股票未来发展的趋向[1]。自回归模型是时间序列模型中最常用的一种模型，能较为直观的描述股票价格的动态变化[2]。由于AR(p)模型在拟合的过程中无法进行变量剔除，Tibshirani(1996)[3]提出了Lasso回归方法,通过构造一个惩罚函数得到一个简化模型，将一些回归系数压缩至零。Nardi Y(2011)[4]等对Lasso回归方法进行数据模拟和实证研究，发现Lasso回归方法适用于AR(p)时间序列模型的参数估计和阶数选择。Zou(2006)[5]对Lasso方法进行改进，在L1项的惩罚系数前加自适应权值，提出了自适应Lasso法。谢仪(2014)等[6]利用数据模拟发现自适应Lasso方法在AR(p)模型估计中具有实用性。但Lasso系列方法仍存在一些不足，比如:当数据具有很强的共线性时，它的选择效果会减弱。因此，Zou(2005)等[7]提出了Elastic Net回归模型：将L1和L2惩罚项进行凸线性组合。

纵观上述已有研究结果，多数学者都论证了Lasso类方法在自回归时间序列模型中的适用性，受此启发，本文将弹性网方法应用于AR(p)模型中，并比较弹性网方法、Lasso方法以及ALasso方法对AR(p)模型预测效果的改进性。

二、模型简述

考虑自回归模型AR(p)：

yt=β0+β1yt-1+β2yt-2+…+βpyt-p+εt

(1)

针对模型(1),可通过最小二乘法构造二次损失函数，最小化期望损失可得模型的参数估计结果：

(2)

虽然上述模型通过简单求偏导即可得到参数估计结果，但其结果易受自变量相关性强弱的影响，Tibesirani(1996)[3]提出了Lasso方法，在(2)中加入L1惩罚项,使模型的一些参数收缩至零，同时实现变量选择和参数估计，其参数估计表示为：

(3)

(4)

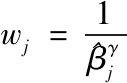
Lasso类方法虽然具有良好的变量选择性质，但会出现过度压缩的情况，实际应用中，人们更希望将所有与被解释变量有关的影响变量包含在内。基于上述考虑，Zou(2005)等[7]提出了Elastic Net方法，该种方法将L1正则项和L2正则项均加进惩罚项中，具体参数估计形式表现为:

(5)

观察式(5)可以看出(3)和(4)均是其特例，因此Elastic Net方法也具有变量选择的特点。考虑到弹性网方法的综合性，本文就采用此方法对AR(p)模型进行参数估计。

三、实证研究

(一)数据处理

本文选取2017年1月1日至2019年11月31日的上证综合指数的日收盘价作为建模数据，将2019年12月前十个交易日的收盘价作为模型测试数据。本文数据来自于新浪财经(https://finance.sina.com.cn)。根据所选区间内的上证综指日收盘价绘制出如图1所示的样本时间序列图，从图1可以看出，该样本数据有明显的波动趋势，总体呈现先下降后上升的态势，由此初步判断数据并不平稳。

图1 上证综指日收盘价格时序图

然后对数据进行详细的描述性统计分析以及正态性检验，结果见表1。由表1可看出，整体数据的偏度系数大于零，峰度系数不等于3，且J-B统计量的结果为15.924，表明该样本序列不服从正态分布。进一步对其进行单位根检验，所得ADF检验对应p值为0.709，说明该序列确实不是平稳的。

表1 上证综指日收盘价的描述性统计

本文对上证综合指数的日收盘价进行一阶差分处理，再对其做平稳性检验，得到的p值是0.01，表明差分后的数据是平稳的。因此，本文以上证综指的日收盘价的一阶差分值作为模型的被解释变量，可记作yt,其滞后p阶的一阶差分值作为解释变量，以此建立自回归模型。

(二)模型建立

为了精准地确定AR(P)模型的阶数，本文选用AIC定阶准则，利用R软件绘制出各阶模型的AIC取值图。从图2中也可以明显地看出，当P取7时模型的AIC值最小，因此本文最终选择AR(7)模型。

图2 AIC值点线图

模型定阶以后，本文依次运用Lasso，ALasso，Elastic-net方法对AR(7)模型进行变量选择处理，得到具体的模型估计结果见表2。从表2的数据可以看出，自适应Lasso方法下的变量个数更少，说明这种方法对变量进行了过度选择，会删除某些对被解释变量有影响的因素。

表2 三种方法下变量选择以及参数估计结果

三种模型建立以后，我们对拟合模型进行充分性检验。其残差序列白噪声检验的p-value以及检验结果见表3。从3可知，三种方法下对应的检验p值都大于0.05，无法拒绝原假设，说明这三个模型对数据的建模是充分的，我们可以选择上述的三种模型对yt进行样本外预测。

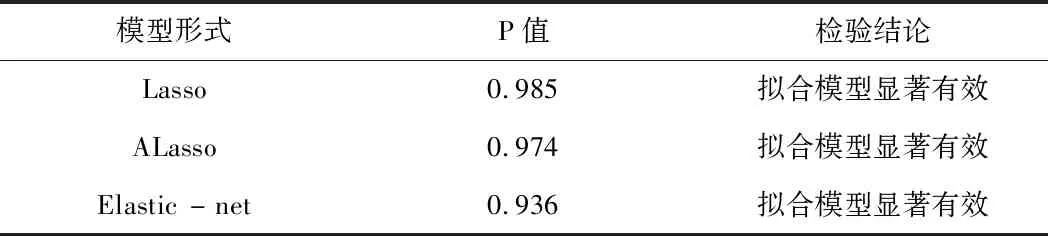
表3 三种方法下的拟合模型的Ljung-Box检验结果

(三)模型预测

接下来本文利用上述三个模型对2019年12月前十个交易日的日收盘价进行估计，并利用平均绝对误差计算预算精度，具体结果见表4。根据表4可以发现，应用弹性网方法得到的估计值有5天更接近真实值，预测效果优于其他两种方法。尤其是第7天的股票预测值里，Elastic-net方法得到的绝对误差仅为1.881。综合比较三种模型的预测效果，弹性网方法的MAE值最小为12.995，明显小于Lasso方法和ALasso方法，说明通过弹性网方法得到的AR(7)拟合模型的预测效果最佳，也表明在与自适应时间序列模型的结合中，弹性网方法的参数估计能力优于Lasso类方法。

表4 上证综指19年12月前十天日收盘价估计结果

四、结论

在对自回归模型进行变量选择上，Lasso类方法可以有效实现，但考虑到Lasso类方法系数收缩的极致性，本文提出了弹性网方法与自回归模型的结合。通过对上证综指2017年1月至2019年11月间日收盘价的一阶差分值建立AR(7)模型，运用Lasso方法、ALasso方法和弹性网方法进行变量选择以及参数估计，进而对2019年12月前十个工作日的日收盘价进行预测，结果表明：综合了L1和L2正则项的弹性网方法在模型预测效果上明显优于其他两种方法，预测误差最小。弹性网方法与AR(p)模型的结合是探究时序模型的新思路，一方面它的变量选择性能可以简化传统时序模型，另一方面也能提高模型的预测能力，对以后的股票价格预测具有重要的现实意义。当然，弹性网方法与自回归模型的结合也可扩散至对其他时间序列数据的研究，这对今后的时间序列模型的发展具有很好的借鉴意义。