井震结合统计学反演方法在薄层砂体预测中的应用
2020-11-20那晓勋
那晓勋
(华北地质勘查局 五一四地质大队,河北 承德,067000)
地质统计学反演由Haas提出,Dubrule和Rowbothman加以发展,它是通过测井数据和地震数据,在井震精细标定的基础上,通过变差函数计算得到的初始阻抗模型正演,与地震数据体反复迭代,得到最终储层预测模型。其核心思想结合了地震平面预测趋势和井数据纵向较高分辨能力的优势,采用特定的统计学算法,实现地下目标体的三维空间预测[1-2]。目前,地质统计学反演在国内外油田的储层描述中得到了广泛的应用,有效提高了储层描述精度,提高了勘探开发的效果。随着地质统计学反演方法研究和应用的深入,虽然在应用领域逐渐扩展,但对影响其实际效果的因素分析相对较少。同时,针对陆相薄互储层的预测尚缺少系统性的研究[3-5]。基于井震结合统计学反演的陆相薄互储层预测方法研究,以松辽盆地北北二区块为研对象,通过对比不同反演方法的特点,总结统计学反演的优势和影响因素,形成反演关键环节的处理手段,实现陆相薄储层精细描述。
1 研究区概况
北北二区块位于松辽盆地东北部,属陆相河流-三角洲相沉积体系,划分为分流平原、内前缘和外前缘三种亚相,储集层以细砂岩、粉砂岩、泥质粉砂岩为主,纵向上砂泥岩呈薄互层分布,如图1所示。

图1 研究区储层沉积特征Fig. 1 Sedimentary characteristics of reservoir in study area
北北二区块发育高台子、萨尔图及葡萄花三组含油系统,总厚度约400 m,包含8个油层组、100个小层。具有3种类型油层,Ⅰ类油层是平面大范围沉积的高渗透油层,即葡Ⅰ1-2砂岩组,空气渗透率1 654×10-3μm2,有效渗透率465×10-3μm2;Ⅱ类油层是区域沉积的中-低孔渗性油层,平均渗透率425×10-3~890×10-3μm2,有效厚度大于3 m的钻遇率在65%以上;Ⅲ类油层是呈条带状、局部分布的低孔渗油层[6-8]。
由上述分析可知,研究区整体储层较薄,横向分布零散,单纯依靠井资料预测井间储层砂体存在难度,迫切需要开展地震反演储层预测,通过井震结合实现陆相薄储层精细描述,为油田的后续精准开发提供地质基础。
2 井震结合统计学反演预测
井震结合统计学反演是通过测井数据和三维地震数据,在井震精细标定的基础上,在框架模型的约束下,通过变差函数计算得到的初始阻抗模型正演,与地震数据体反复迭代,输出反演预测模型,其技术流程如图2 ~ 4所示。首先通过已知点和未知点的距离(滞后距h),统计得到变量孔隙度的变化规律,并利用地震正演控制实现变量空间模拟计算。

图2 已知孔隙度数据及待模拟位置Fig. 2 Known porosity data and location to be simulated
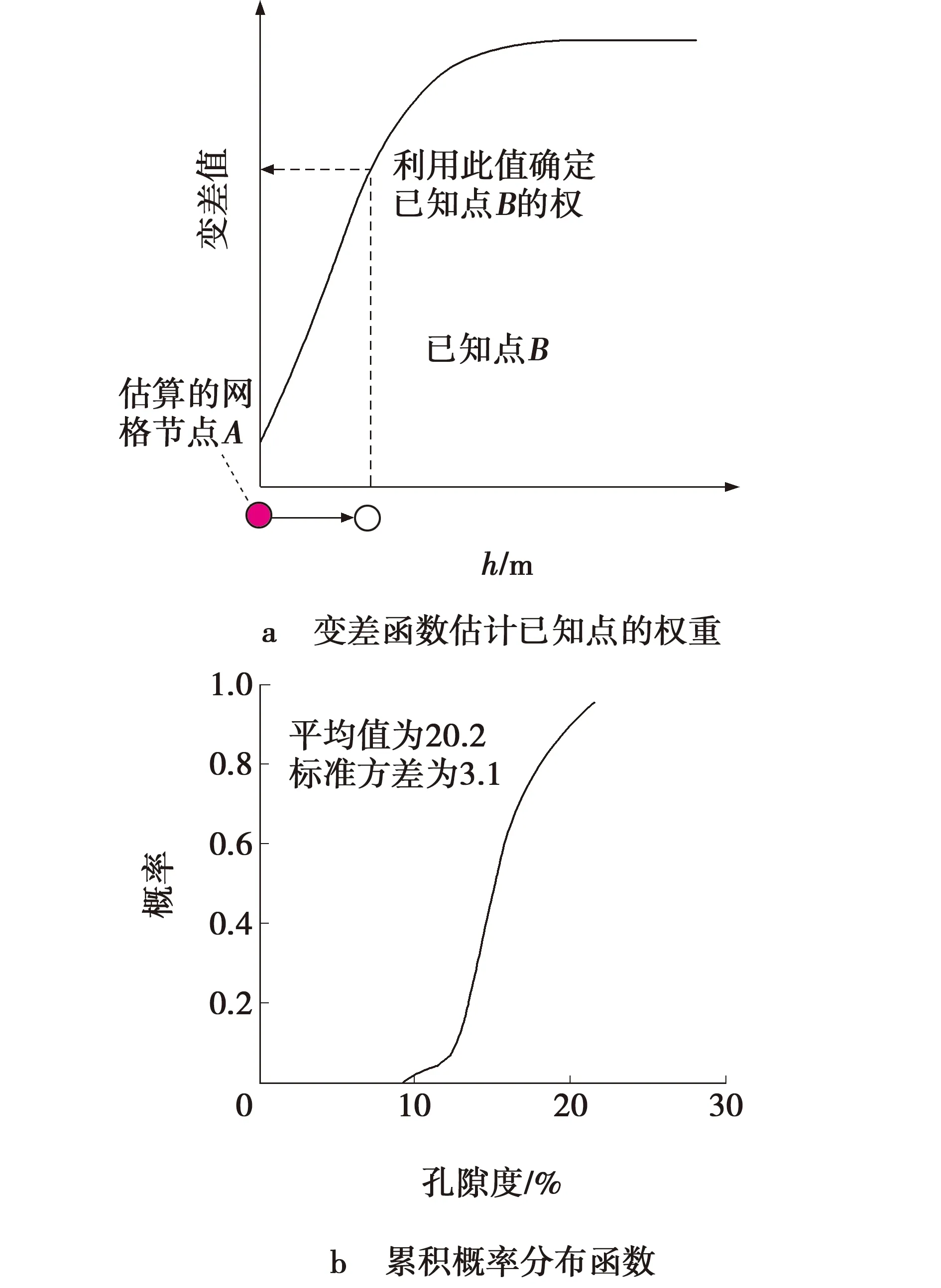
图3 变差函数及概率分布函数Fig. 3 Variogram and probability distribution function
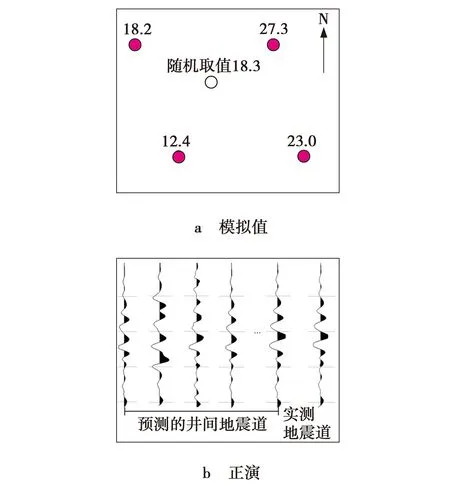
图4 空间模拟及正演质控Fig. 4 Quality control of space simulation and forward modeling
2.1 测井曲线标准化
由于研究区包含五期井网,时间跨度最长达60余年,不同测井仪器序列差异大,导致测井曲线对同一套储层反应幅度差异大,需要选取标准层和标准井进行标准化处理。
一般认为一套标准层,不同井点的声波曲线必须具备相近的变化规律和起伏特征,因此,标准层应该沉积平稳,厚度大于4 m;岩电性特征稳定和有利于大范围追踪对比的特点。选 SⅠ-SⅡ层的泥岩层作为标准层,选用L7-J17井作为研究区标准井,利用直方图校正法对研究区曲线进行了标准化处理。首先对曲线进行平滑滤波处理,再根据各井标准层的直方图数据读出特征峰值,然后将所有井的特征峰值与标准井L7-J17的特征峰值作比较,便得出各井的校正量。测井曲线标准化前、后对比直方图如图5所示,将研究区内多井进行标准化处理并进行对比,声波时差测值校正后消除了随机干扰等误差,可以取得较好的校正效果[9]。

图5 测井曲线标准化前、后对比直方图Fig. 5 Histogram of comparison before and after logging curve standardization
2.2 井震精细标定
井震精细标定是井数据和地震数据在同一域内进行地震反演的前提和基础,影响着反演结果的精度。常规方法是将声波阻抗与子波进行褶积计算,生成合成地震记录,将合成地震记录与井旁道地震进行匹配,通过上下调整对应关系,实现井震精细标定。如图6所示,由图6可以看出,各套波组对应关系较好,井震相关性达80%以上,完成了精细储层标定,确保了后续地震反演储层预测的可靠性。
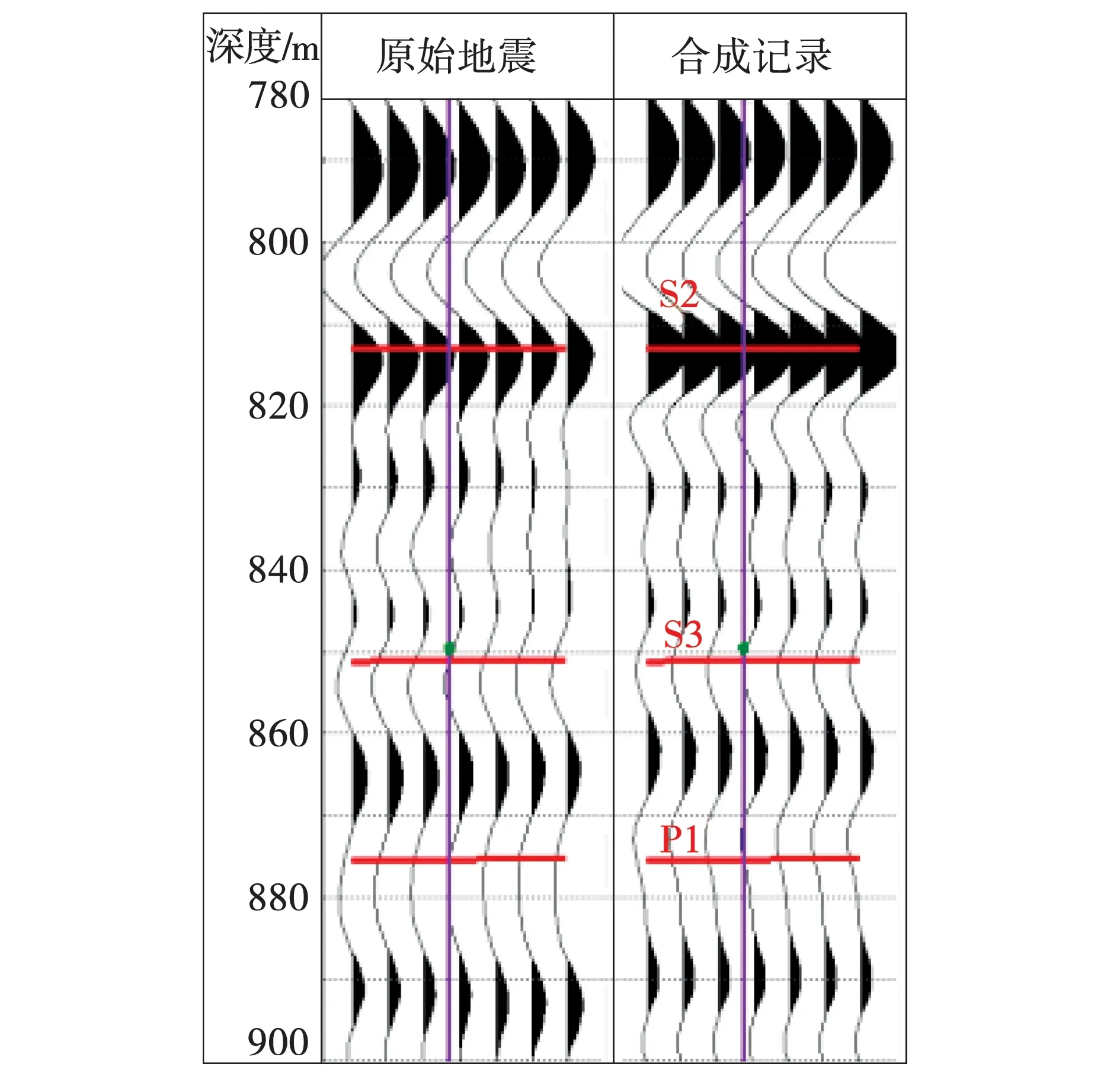
图6 井震精细标定剖面Fig. 6 Well seismic fine calibration section
2.3 框架模型
反演框架建模采用两步走:一是油层组层面建立,二是小层层面建立。油层组级别层面是基于地震解释层面;小层构造面的建立主要通过井震结合,即用地震面做约束,用井上分层数据插值得到的层面。该方法得到小层层面既符合钻井分层数据,也与油层组地震解释层面形态保持一致。在小层构造模型的基础上还需进一步进行垂向网格的划分,垂向上平均每个网格厚度为0.50 ms,经网格细化后,研究层段垂向上总共划分为568个网格,最终建立了构造体模型,如图7所示。研究区属于喇嘛甸背斜构造的一部分,西翼比较陡,地层整体趋势上没有大的突变,局部形成地堑式构造。
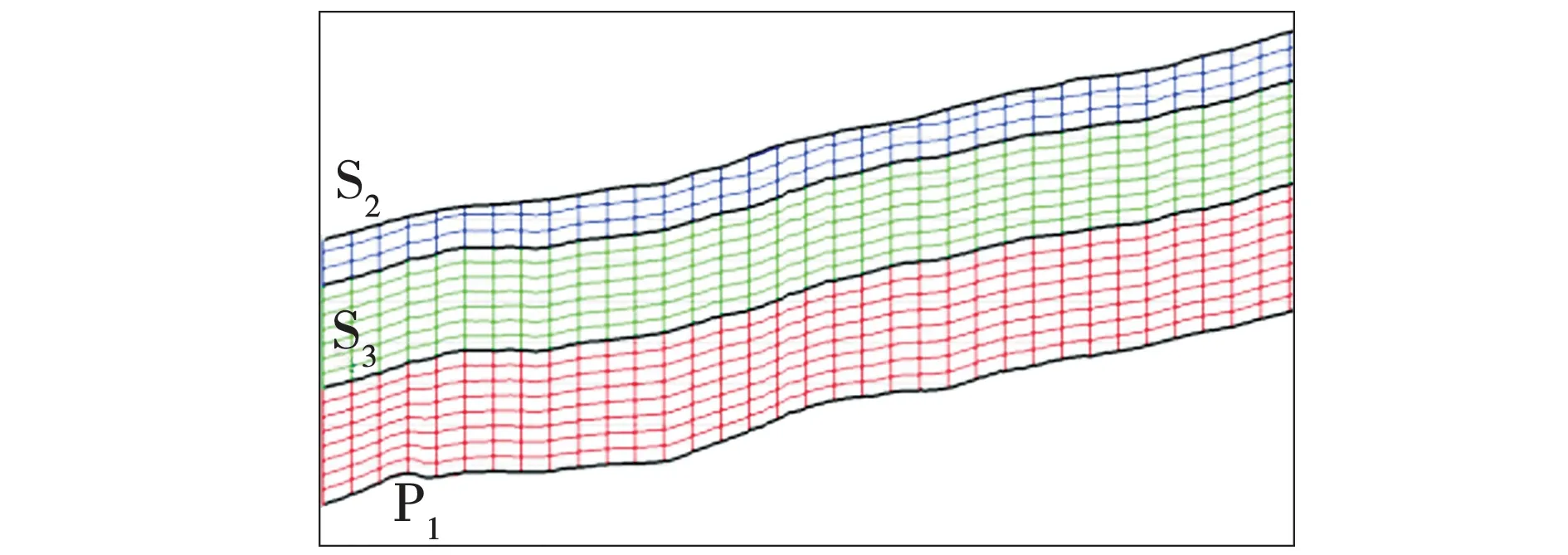
图7 研究区网格模型剖面Fig. 7 Grid model section of study area
2.4 变差函数
初始波阻抗模型是基于井数据的阻抗曲线,利用变差函数空间外推实现的。变差函数的准确求取,直接影响初始模型的精度,而且影响后续反演储层预测的效果。
变差函数通过井数据拟合得到,图8为通过井数据拟合得到的三维变差函数图,图中离散曲线为实验变差函数,连续曲线为理论变差函数,在变差范围内理论模型与实际变差函数吻合度越高越好,且实验变差函数越光滑越好。
2.5 地震采样间隔
采样间隔是指地震反演的结果在输出时给出的采样间距,输出采样间隔将直接影响反演结果的精细程度。研究中通过不同采样间隔输出的方式来对比反演结果,以此来验证采样间隔对反演结果的影响大小,并寻找合适的输出采样间隔。不同采样间隔的反演结果对比如图9所示,由图9可以看出,预测结果总体上变化不大,但在预测较薄的储层时较小的采样间隔所反演的结果更加精细。通过对反演结果的数据进行分析可以发现,反演结果的时间域厚度是以采样间隔的整数倍给出,因此,较小的采样间隔所取得的数据也更加精细。简而言之,1.00 ms采样间隔输出的结果最小预测厚度约为1.5 m的砂岩,0.50 ms采样间隔输出的结果最小预测厚度约为0.8 m的砂岩,本次采用的0.25 ms 采样间隔输出的结果则可以预测约0.4 m厚的砂岩。因此,在薄层砂及砂泥薄互层较发育的地区进行储层预测时,以0.25 ms的采样间隔可以有效提高薄层及薄互层的预测精度。同时,在反演效果较为精细时,采用较小的采样间隔显示效果也会更好[10]。

图8 三维变差函数Fig. 8 Three dimensional variogram

图9 不同采样间隔剖面对比Fig. 9 Comparison of profiles with different sampling intervals
3 反演结果分析与评价
图10为井震结合统计学反演结果剖面,同时列出了常规的确定性反演和测井属性反演结果剖面。由图10可以看出,地质统计学反演结果的纵向分辨能力较高,横向能够反映储层的非均质变化,并且与测井曲线符合较好,直观反映了地质统计学反演方法的精度。
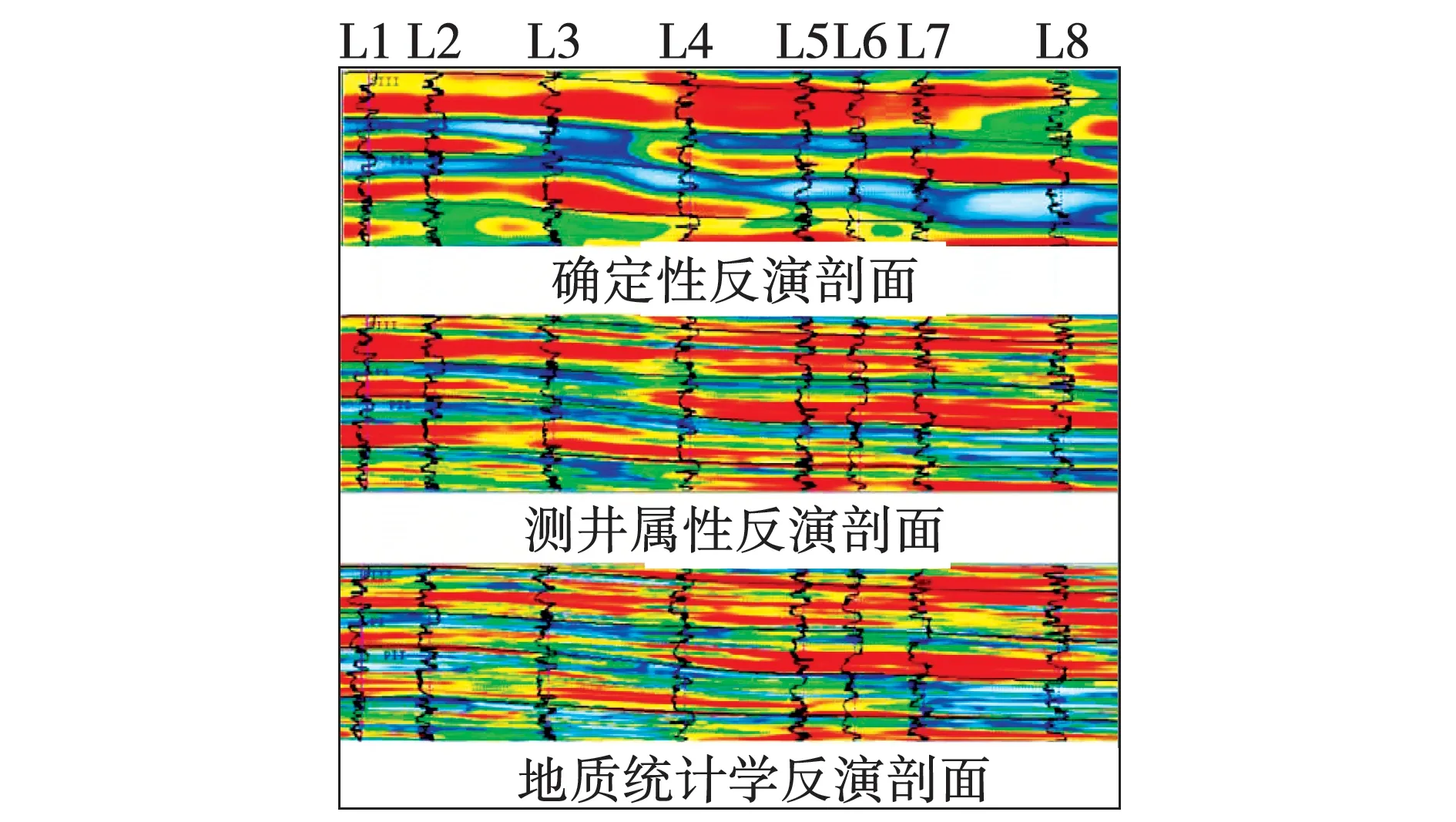
图10 井震结合统计学反演结果对比Fig. 10 Comparison of well seismic and statistical inversion results
根据研究区50口后验井检验反演精度的统计数据,厚度2.0 m以上砂体预测符合率到达85%以上(常规基于井的预测精度78%),厚度1.0 m以上砂体预测符合率到达70%以上(常规基于井的预测精度62%),表明该方法在陆相河流-三角洲薄储层精细描述方面具有理想效果,对于其它油田也起到了示范作用。
4 结 论
井震结合统计学反演结果纵向分辨能力较高,横向上能够反映储层的非均质变化,并且与测井曲线符合较好。根据50口后验井统计数据,厚度2.0 m以上砂体预测符合率到达85%以上,厚度1.0 m以上砂体预测符合率到达70%以上,该方法对薄储层描述具有较高精度。
文中方法满足陆相河流-三角洲薄储层的精细描述,对于其它油田的储层精细描述也起到示范作用。但使用中应注意几个关键环节,需要做测井曲线标准化、精细井震标定、框架模型及变差函数拟合,注意合适的地震采样频率,才能保证反演预测效果。
