轨迹分析方法与长短期记忆网络的电网暂态稳定裕度评估

薛 易，闫 旭，郭松林，相东昊

(黑龙江科技大学 电气与控制工程学院，哈尔滨 150022)

0 引 言

随着电网中新能源占比不断提高，电力电子化现象日益凸显，加剧了电网运行环境的复杂特性[1]。目前，电力系统暂态稳定评估手段大多依据轨迹分析方法，其耗时较长，难以满足大电网正常态运行的可靠性与时效性要求[2]。暂态稳定评估作为稳定性研究的主要方向[3]，如何在电网故障恶化前期精准定位暂态能量边界并确定系统稳定裕度对维持电网安全稳定运行具有现实意义。

随着广域量测系统(Wide area measurement systems，WAMS)的大面积推广应用[4-5]，电网量测信息的全局性及时效性得以满足，拓宽了电力系统暂态稳定性研究的应用前景。现阶段有关电网暂态稳定性的研究大多结合轨迹预测、轨迹判据以及人工智能等方法分析响应信息。林飞等[6]通过构建发电机转子间相对摇摆角的多项式模型预测轨迹信息，计算简单，但预测结果的准确性受限于模型参数及阶数。吴为等[7-9]基于轨迹的几何特征变化判别电网稳定性，计算速度快，但其结果能否有效受量测信息精度的影响较大。

近年来，人工智能技术受到各界的广泛关注，凭借其学习机制可以挖掘电网数据间深层关联关系，揭示系统状态与响应信息间的内在联系，具有精度高、时效性强，现已被广泛应用于电网领域[10-13]。常用的人工智能技术主要包括卷积神经网络、支持向量机等。安军等[14]通过对响应信息的排列组合建立电网状态同量测信息间的精准映射关系，摆脱了传统方法对模型的依赖，但信息间的作用机理尚不明晰，对于复杂电网的预判存在误差。

长短期记忆网络具有自主学习数据特征和抽象表达等特点，可有效解决多时间断面内存在的长依赖关系问题[15-17]。凭借其特有的网络结构，对电网强非线性响应信息进行自主学习，与传统评估手段相比，具有更高的精度与可靠性。基于上述分析，笔者提出了一种电力系统暂态稳定裕度评估方法，仅依靠电网实测信息，结合轨迹分析方法[18]及长短期记忆网络，利用仿真算例建立响应信息同电网状态间的映射关系，通过多重响应信息的组合，使预测结果具有更高的鲁棒性，提高暂态稳定评估的精度，运用IEEE-39节点系统验证所提方法的有效性。

1 电网暂态稳定裕度评估

电力系统具有时变、高度非线性的人造物理系统，其量测信息具有复杂化和多元化的特点，致使常规电力系统暂态稳定评估方法的时效性以及精度降低。笔者结合人工智能技术，构建了如图1所示的电网暂态稳定裕度评估体系。该评估体系基于向量测量单元实时采集系统响应信息，数据接入离线训练好的长短期记忆网络评估模型，在线给出暂态稳定裕度。

图1 电力系统暂态稳定裕度评估体系Fig. 1 Power system transient stability margin assessment system

长短期记忆网络是递归神经网络中的一种，可根据时间序列进行自我调节，通过特殊的记忆单元实现对过去信息的记忆，能够有效解决预测过程中存在的解决“长依赖”问题。实验数据为受扰电网多时间断面内的时序响应信息，因此,通过长短期记忆网络快速预测未来时间断面内的轨迹信息从而量化系统稳定裕度实属必然。

长短期记忆网络的记忆单元由三个门控制器组成，具体如图2所示，其中，包含遗忘门、输入门、输出门，以及代表信息流动的信息链。这些门控制器可以对输入的电网量测信息进行深入挖掘并自主记忆，从而更精准的实现对电网未来时间断面内的轨迹预测问题。

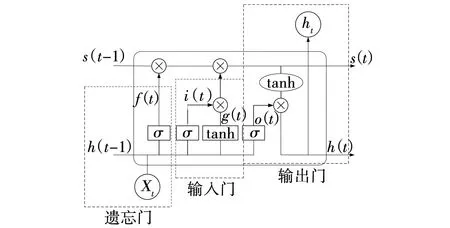
图2 LSTM节点内部示意Fig. 2 LSTM node interior

长短期记忆网络记忆单元的读取与修改主要通过上述门控制器加以实现，保证对信息链进行实时更新迭代。通过输入不同故障类型下的电网发电机功角、电压幅值以及有功无功功率数据，提高模型的泛化能力。

1.1 遗忘门

遗忘门控制器通过相应的门控措施决定记忆单元状态中冗余信息的去留，量测信息中并非全部都能够建立同电网状态间的映射关系，因此，需要通过遗忘门的遗忘机制进行剔除。遗忘门计算公式为

f(t)=σ(wfxx(t)+wfhh(t-1))+bf，

式中：bf——偏置量；

σ——sigmoid函数；

x(t)——t时刻输入记忆单元的受扰电网轨迹信息；

h(t-1)——t-1时刻记忆单元输出的轨迹信息；

wfx、wfh——遗忘门与输入信息、输出信息的权重。

1.2 输入门

输入门控制器通过相应的门控措施配合激活函数对受扰电网量测信息进行处理，保证记忆单元能够更好地学习记忆。输入门计算公式为

i(t)=σ(wixx(t)+wihh(t-1))+bi，

式中：wix——输入门与输入信息权重;

wih——输入门与输出信息权重;

bi——偏置量。

由图2可见，输入门中，输入信息x(t)以及上一层的输出信息h(t-1)经由激活函数tanh得到g(t)，为记忆单元的候选状态，计算公式为

g(t)=φ(wgxx(t)+wghh(t-1))+bg，

式中：bg——偏置量；

φ(x)——激活函数；

wgx、wgh——输入门和控制器连接输入信息、输出信息权重。

1.3 输出门

输出门控制器通过相应的门控措施将有用的电网量测信息输出并进行下一次迭代学习，输出门计算公式为

o(t)=σ(woxx(t)+wohh(t-1))+bo，

h(t)=s(t)o(t)，

式中：bo——偏置量；

h(t)——隐含层输出值；

wox、woh——输出门控制器同输入信息、输出信息间的权重。

2 稳定裕度预测模型

2.1 输入特征构建

输入特征构建的合理与否会影响最终模型的评估性能，考虑到输入特征既要有效地反应系统的暂态过程，还要具备可以实时采集的条件，且维数不会随着系统规模的增大而增加，因此,文中选用发电机的功角、电压幅值以及有功无功功率作为预测模型的输入信息。同时结合“三段式”特征与受扰后轨迹特征的优点，构建了一种全阶段时间序列特征，以有功为例，如图3所示。

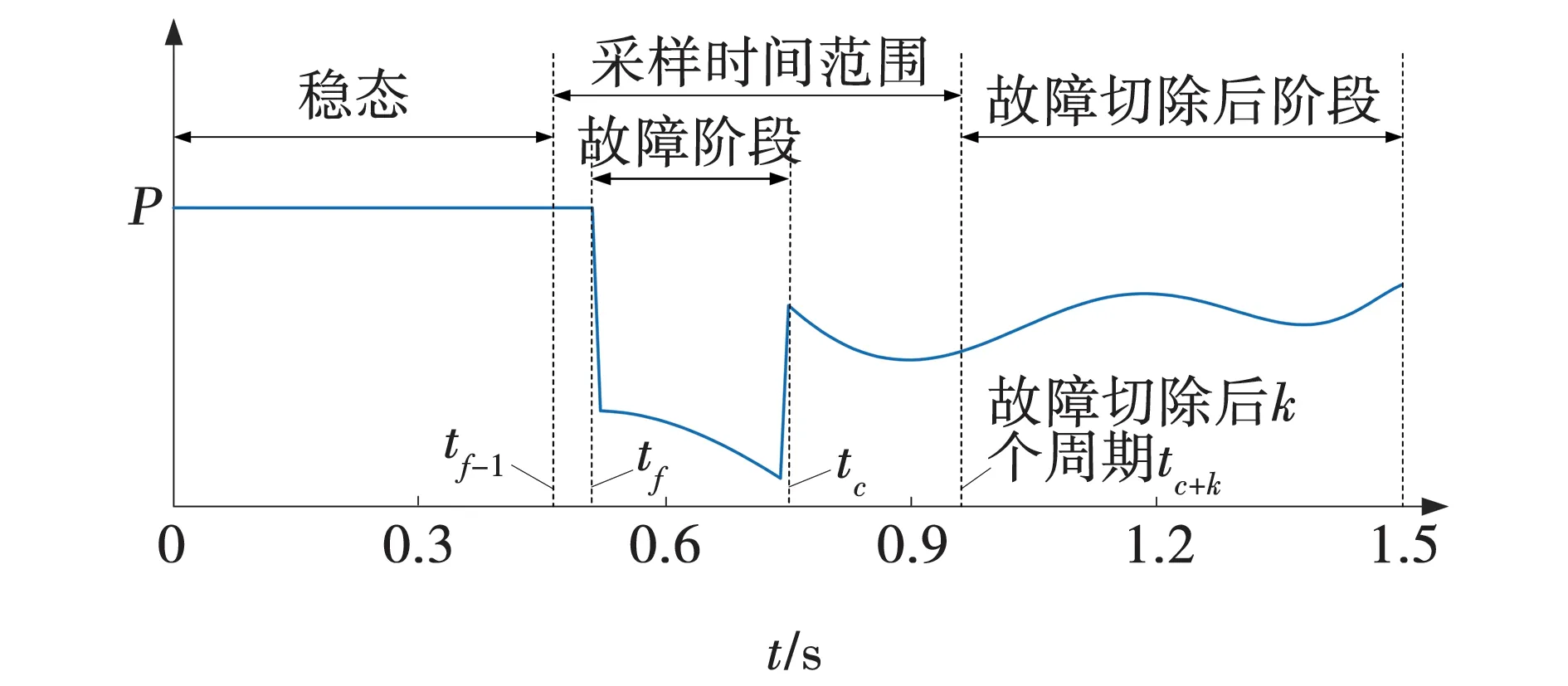
图3 输入特征采样时间Fig. 3 Input feature sampling time

通过排列组合发电机状态量电压、功角、有功功率、无功功率构建输入特征，采样时间从稳态时刻一直延续到故障切除后的第k个周期，采样区间间隔为[tf-1,tc+k]。其中tf为故障发生时刻，tc为故障切除时刻，记故障发生前一个周期的tf-1时刻为稳态时刻。

由于在不同扰动条件下tc时刻不同，会导致故障切除前序列长度不同。为了方便对模型进行训练，以tc时刻前最长长度为基准，为保证时序信息序列维度相同，对短序列样本进行补0操作。而此操作对特征提取贡献度为零，因此，以LSTM能自动甄别时间序列中的有用信息。

2.2 输入数据预处理

输入特征的全信息矩阵包含电网多个状态信息，其量纲各不相同，因此，有必要在输入长短期记忆网络前对输入信息进行相应的处理。输入信息计算公式为

式中：xg——经过归一化处理后的输入信息；

maxx、minx——待归一化变量的最大值与最小值。

为充分挖掘时序信息的演进规律，将相邻时刻各特征的变化率一同作为输入量，以有功功率为例，其变化率数学表达式为

式中：xt———当前时刻的有功大小；

lt———有功功率的变化率。

基于上述分析结果，构建三维输入信息矩阵，结构如图4所示。

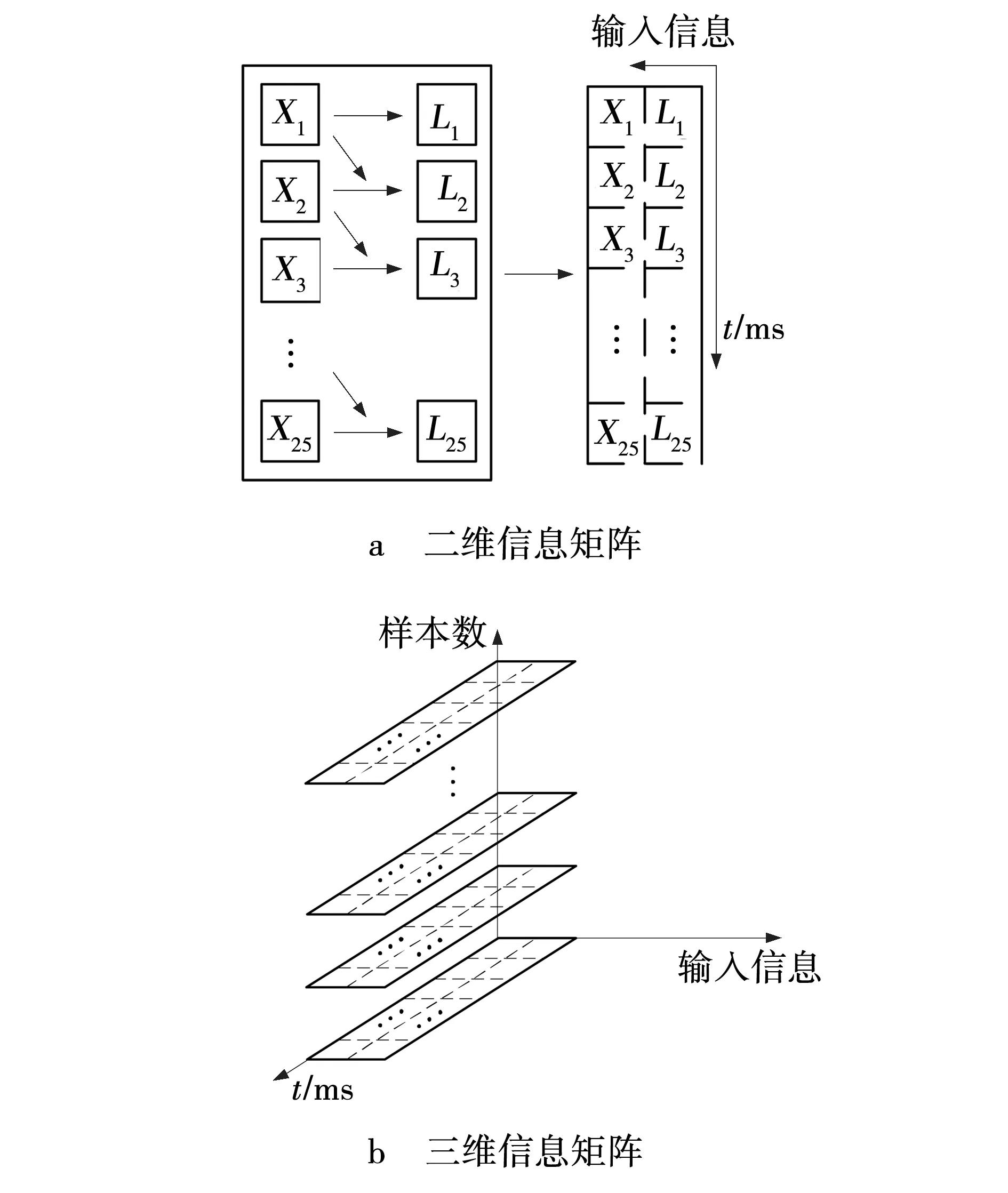
图4 输入信息排列组合Fig. 4 Composition of input information

图4a中X1→Xn代表某故障下的受扰轨迹信息；L1→Ln表示代表输入信息的变化量，进行相应的排列，构建如图4a所示的二维矩阵形式。为满足训练学习样本空间的要求，纵向延展其样本数量，构造图4b所示的三维信息矩阵。

2.3 稳定指标构建

从能量角度，利用轨迹分析法构造暂态稳定裕度指标。

2.3.1 数学模型

电力系统的机电暂态过程中，影响暂态稳定性的主要是各发电机之间的相对摇摆，因此,将系统模型交换至惯性中心坐标系下，以惯性中心(Center of inertia,COI)坐标系下的发电机转子运动方程作为微分方程组，则有

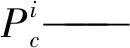
Mi——发电机i的惯性时间常数；

ωN——额定角速度。

发电机的能量函数定义为

Vi(t)=VKi(t)+VPi(t),

式中：VPi———发电机i的势能；

VKi———发电机i的动能。

2.3.2 稳定、不稳定指标

根据暂态稳定的概念，若发电机i稳定，则其势能立即增加，与此同时动能开始向势能转化，且未完全转化。若注入动能不能被全部转化，则代表该发电机会在第一摆的过程中失去稳定。针对一般故障而言，发电机在故障后的势能增长期间具有单调递增的特点，且峰值逐步降低，即第一次到达峰值时的势能为最大势能点，此类状态轨迹被称为规范轨迹。

对具备规范轨迹的受扰系统发电机的能量进行分析，假设故障切除时刻为tc，对单台发电机的势能最大与最小对应时刻为

若发电机i的受扰轨迹为规范轨迹则其势能曲线最低点所对应的时刻为

相应的发电机i势能曲线最高点所对应的时刻为

对于具有规范轨迹的发电机i，当其稳定或不稳定时，势能VPi沿势能曲线变化情况如图5所示，图中，θia=θi(tai)，θib=θi(tbi)，θir为θi的临界值。

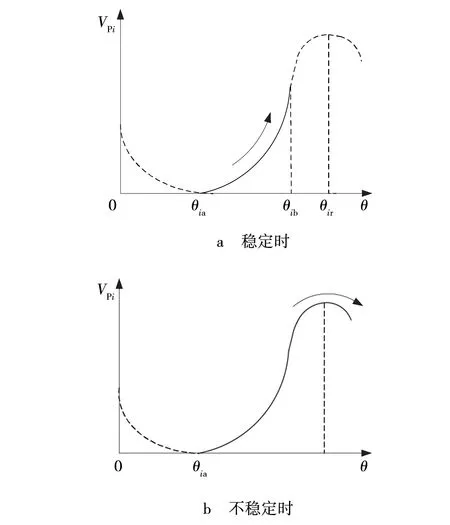
图5 发电机的轨迹特点Fig. 5 Trajectory characteristics of generators

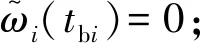
因此，若受扰系统发电机i状态轨迹为规范轨迹，则势能达到极值点是对应的稳定与不稳定指标为

由上述定义可知，稳定指标Si趋于零只有在对应发电机失稳的情况下才会出现，而Si的符号仅表明了发电机在第一次势能增加过程中的运动方向(加速/减速)。因此，文中将系统中各台发电机稳定指标的绝对值，作为稳定裕度，以最小值作为LSTM的输出。该稳定指标完全不依赖任何临界能量，指标数值随稳定性的恶化而单调下降，固定临界值0便于辨识发电机距离临界稳定区域的距离，完全优于Found等提出的指标。

2.4 模型性能的评价指标

利用准确率A、漏判率M和误判率F评价神经网络的暂态稳定区分能力，其数学表达式为

式中：ntp——稳定算例正确评估的样本个数；

nfP——误判样本数，代表失稳样本被错误评估；

ntn——失稳样本正确评估的样本个数；

nfn——漏判样本数，代表稳定样本被错误评估。

A准确率代表正确分类数的比值大小，表征对于某种故障引起的状态是否能够预测准确。F表示对于某种故障造成的失稳没有报警，而是预测为稳定状态。M表示对于某种故障不会引起系统失稳，但是模型却因预测为失稳状态而报警。对于运行中的电力系统，若将失稳样本误判为稳定样本，而不采取任何控制措施，使运行人员错过调整运行方式的最佳时间，将会给系统带来灾难性的后果，必须力求避免。若将稳定样本漏判为失稳样本，则会导致虚警，给工作人员增加工作量，但对系统安全稳定性的影响相对误判稳定而言要小很多。

评价模型预测精度的指标计算公式为

式中：err——平均误差；

N——样本总容量；

Pi——第i个样本算例稳定或不稳定指标的预测值；

ri——第i个样本算例稳定或不稳定指标的实际值。

3 算例分析

3.1 数据集构造

通过IEEE-39节点系统验证所提方法的有效性，系统内包含10台发电机、39条母线、46条支路，系统频率设定为额定频率50 Hz，系统如图6所示。

图6 IEEE-39节点系统Fig. 6 IEEE-39 nodes system

算例由综稳PSASP仿真软件得到，系统内发电机均为恒阻抗模型。基于测试系统的发电水平和负荷水平在80%～120%波动。每种运行方式下设置三相短路故障，故障位置位于为34条线路的10%～90%处。设置故障发生在1 s末，切除时刻在1.8～2.2 s之间。通过轨迹分析法计算各样本的最小发电机稳定指标，对样本标签进行标注。共获得10 200个运行样本，其中失稳样本4 054个、稳定样本6 146个。

3.2 模型分类性能对比

将样本集合分为训练集、测试集与验证集，对应比例为8∶1∶1。为综合比对长短期记忆网络模型能有效评估受扰系统稳定性并得出稳定裕度，对比分析LSTM同DT、KNN以及SVM各模型在相同的训练集和测试集上进行暂态稳定评估。其中，DT采用C4.5算法，为保证评估效果的稳定性，置信因子采用默认值0.25，确定最优超参数为c=3、γ=0.005，KNN采用欧氏距离对待分类样本进行计算。SVM采用径向基函数作为其核函数，其中，最优结构参数的确定方法，采用5折交叉验证和网格搜索法。不同模型的评价结果如表1所示。

表1 不同模型的评价指标

从表 1 可以看出，LSTM模型的评估准确率最高，且误判率和漏判率均低于其他模型，尤其是误判率较其他网络有明显的降低，说明长短期记忆网络可以通过其学习机制深度挖掘时序信息间的关联关系。另外，SVM 的准确率比LSTM低了0.75%，说明了传统机器学习方法在数据挖掘中的短板。DT与KNN两种模型在准确率、误判率、漏判率上均不如其他两种模型，更充分表明了传统方法在分类上难以匹配现今高维非线性电力系统。

3.3 不同响应时间对模型的影响

响应时间反映的是故障清除后的时间，响应时间越长越利于系统稳定控制的实施，相反，如果响应时间较短，则电网运行人员的可操作时间越长，因此希望在尽量缩短响应时间的同时使评估结果准确。通过设置k以获得不同的响应时长的样本算例，相应的暂态稳定评估结果如图7所示。

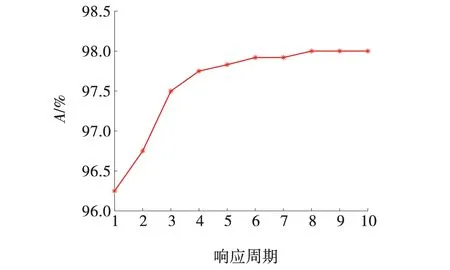
图7 不同响应时间下的暂态稳定评估结果Fig. 7 Transient stability assessment results with different response time

由图7可知，当响应时间为6个周期100 ms时，模型准确率已达到97.92%。继续增大采样周期，模型预测性能基本接近。综合考虑计算速度和预测性能，响应时间设为6个周期可满足实际使用需求。

3.4 模型指标预测性能

通过LSTM建立了评估输入与发电机稳定指标之间的映射关系，为验证所提模型的指标预测精度，对比分析LSTM与BP网络，图8为BP与LSTM网络对各发电机稳定指标的预测误差。

图8 稳定指标预测误差Fig. 8 Prediction error of stabilization indicators

由图8可知，LSTM网络对各发电机的稳定指标预测精度均明显高于BP网络。以各发电机稳定指标的最小值作为模型的输出，BP和LSTM网络预测的指标平均误差如表2所示。

表2 预测结果评价指标

由表2可以看出，BP网络预测的指标平均误差明显高于LSTM，说明了LSTM具有不错的预测性能，这是因为LSTM相较于BP网络可学习轨迹的时序特征，因而具有更强的拟合能力。进一步随机选取100个测试样本在最严重故障下的稳定指标实际值和预测值如图9所示。

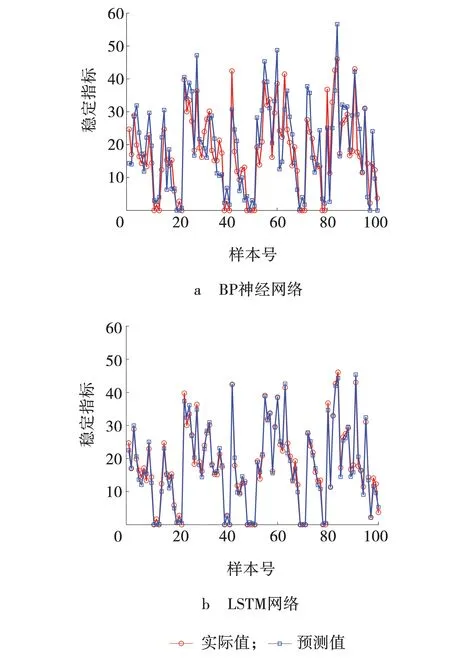
图9 部分稳定指标预测结果Fig. 9 Projections of stabilization indicators

由图9可以看出，LSTM网络通过挖掘大量样本数据，预测样本指标的数据趋势与实际数据的指标趋势相近，而由单层 BP 网络预测的样本指标趋势与实际样本指标趋势有较大误差，对于数据趋势的逼近能力要劣于LSTM稳定指标预测网络。尤其当样本处于临界稳定时，LSTM预测指标的误差要明显小于BP网络，从而大大降低模型的误判率。

4 结束语

提出了一种基于长短期记忆网络的电网暂态稳定裕度评估方法,通过采集全阶段时序特征作为模型的输入，可充分提取电力系统发生故障的时序演进特征。结合轨迹分析方法构建电网暂态稳定评估指标，实现对受扰系统发电机的裕度评估。通过LSTM实现发电机稳定指标的快速预测，所提方法与其他机器学习算法相比较具有更好的泛化能力，可以为电网运行调度人员争取时间并提供决策支撑。