改进康达效应的静电感应粉尘测量装置
2020-11-20刘丹丹黄鹏升景明明温海蔚赵文帝
刘丹丹,黄鹏升,景明明,温海蔚,赵文帝
(1.黑龙江科技大学 电气与控制工程学院,哈尔滨 150022; 2.国网甘肃省电力公司建设分公司,兰州 730050)
0 引 言
随着工业化的飞速发展,尤其是煤矿的掘进和采煤以及其它金属矿山的开采,粉尘的危害逐渐被人们广泛认识,由粉尘引起的尘肺病是危害中国工人健康的最严重的职业病,同时,粉尘对生产、环境、经济效益有着严重影响。为了控制粉尘和预防尘肺病的发生与粉尘爆炸等,有必要对粉尘的浓度进行测定,以评价粉尘的危害程度[1-3]。粉尘浓度测量方法随着测量原理的不同,适用范围也不尽相同,取样法有滤膜称重法、基于β射线的样品测试法、微量振荡天平法等[4-6],非取样有法光透射法、光散射法、电荷感应法、预测流速法等[7-9]。目前煤矿粉尘浓度连续检测主要采用激光散射法,但其光学窗口易污染、气路容易阻塞、维护频繁。
静电感应原理测量粉尘浓度近年来受到国内外学者的重视并有一定成果。其测量装置基本免维护,不存在气路堵塞。许传龙[10]在分析现有静电传感器理论模型的基础上,根据点电荷的思想提出了改进的静电传感器测量模型。陈建阁等[11]利用棒状电极提出了粉尘浓度检测技术,通过实验证明电荷感应法粉尘浓度检测技术具有较好的重复性。刘丹丹等[12-13]根据文丘里效应,提出通过减小现有测量管道的中间部分管径,提高粉尘颗粒的运动速度,增大了高粉尘的静电感应量,获得粉尘浓度与电荷量呈正相关,粉尘颗粒的碰撞几率与电荷量呈正相关[14-17]。笔者应用静电感应原理,利用康达效应,通过在项目组现有的康达管内部勺型管的基础上增加了矩形齿结构,增大粉尘颗粒的运动速度,使其碰撞机率加大,获得相应的电荷感应量,选取最优结构组合,通过仿真实验验证其有效性。
1 粉尘检测装置的设计
1.1 改进装置的设计原理
现有基于静电感应原理的粉尘测量装置为直管管道,由于管道内的气流作用,粉尘在其内部经过一系列的物理活动后产生静电,粉尘产生的静电量可通过测量装置得到,再经过对产生的静电量进行计算,从而得到粉尘的浓度[18]。其结构如图1所示。
在现有直管管道结构简单,操作便利的基础上,设计了一种勺型管与矩形齿结构互相连接的康达效应管道,提高测量装置的准确度。康达效应即平顺流动的流体经过有一定弯度的凸表面时,由原本的流动方向,改为随着凸出的物体表面流动的倾向[19]。

图1 现有直管装置结构Fig. 1 Straight pipe structure of existing
1.2 改进装置结构
依据康达效应,改进项目组先前设计的康达管道,如图2、3所示。
图2 改进前康达管Fig. 2 Coanda effect pipe structure of original

图3 改进后康达管Fig. 3 Improved coanda effect tube structure
由图2可见,d取6 cm、L取16 cm、L1取4 cm、L2取6 cm、L3取6 cm、L4取1 cm。改进现有的康达管结构,在内部效应体L2处增加矩形齿结构,d2为纵向长度,d3为厚度、m为矩形齿个数,d1取长度3.0 cm不变。除增设的矩形齿结构外,改进前后的康达管道参数一致。
2 仿真模型与结果分析
为了实验的结果更为直观清晰,实验将模拟景明明[20]的康达管3D立体模型,并改变内部结构,启动ANSYS FLUENT ,采用3D单精度求解器。设置求解器定义为压力基隐式求解,选择Eulerian模型,黏性为k-ε双方程模型,为加快收敛,求解方案采用SIMPLEC算法来提高收敛性,控制方程采用QUICK差分格式。物性定义空气为主相,定义粉尘为第二相,定义速度入口边界条件,根据模型水力直径及模型单体入口尺寸计算通道入口水力直径,设置Mixture的湍流强度为5,水力直径为0.5,空气流速为4 m/s,粉尘流速为3 m/s,颗粒体积分数为0.015。Volume松弛因子为0.5,其它设为默认。收敛精度设为0.001,设置入口和出口分别为速度入口和自由出流出口[21-22]。网格划分如图4所示。
图4 改进后康达管3D模型的网格划分Fig. 4 Mesh generation of 3D models
2.1 改进管道参数的寻优
由于矩形齿的纵向长度、厚度及个数均会对粉尘颗粒的运动速度造成影响,故现从三个方面分析。首先设置矩形齿结构初始的纵向长度为2.0 cm、厚度为0.2 cm、横向长度为6 cm,矩形齿个数为2个。将矩形齿的纵向长度、厚度、矩形齿个数分别作相应的增加。当一种影响因素改变时,其余两种影响因素保持不变,以此获得纵向长度、厚度及个数的影响度。然后在单因素实验设计方法中选择序贯实验设计,即后批实验需根据前批实验结果进一步优化后序贯进行,直到获取最佳实验结果。
利用ANSYS FLUENT进行仿真,设置粉尘粒径为1 μm。相应速度值如图5所示。由图5可见,纵向长度、厚度、矩形齿个数的改变对原康达管速度的平均增加率为1.53%、5.80%、0.90%。故矩形齿的纵向长度、厚度、个数对速度的影响度排序为:矩形齿个数小于矩形齿纵向长度小于矩形齿厚度。故接下来通过对速度影响的主次顺序来进行矩形齿结构的寻优。
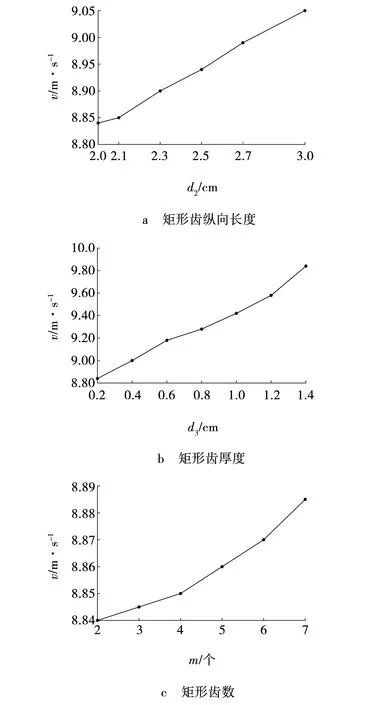
图5 单一影响因素变化对应的速度Fig. 5 Speed corresponding to change of single influencing factor
当矩形齿结构厚度过大时,会将勺型管前端完全覆盖,康达效应效果将会减弱,故厚度不应过大。由图5可知,在0.2~1.4 cm范围内,随着厚度的增加,粉尘颗粒速度逐渐递增,故选择矩形齿厚度为1.4 cm。已知矩形齿厚度为1.4 cm,保持矩形齿个数为2,在1.6~3.0 cm范围内通过仿真分别测得其速度值,如表1所示。由表1可知,当矩形齿状厚度为1.4 cm,矩形齿个数为2时,纵向长度为3.0 cm时,粉尘颗粒速度最大,且纵向长度已达到管最大内径,故选择纵向长度为3.0 cm。
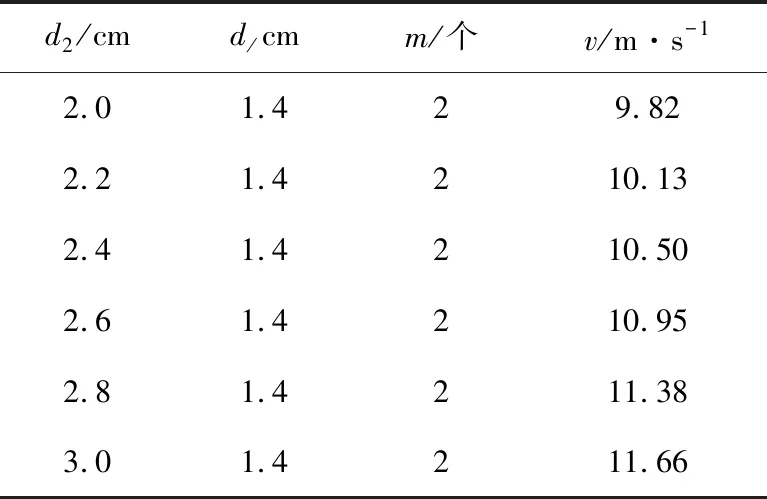
表1 纵向长度变化对应的速度
已知选择矩形齿厚度为1.4 cm,纵向长度为3.0 cm,当厚度为1.4 cm,纵向长度为3.0 cm时,如若选择锯齿个数为7,勺形管的曲面部分将被完全覆盖,此时无法体现出康达效应,故排除。矩形齿个数由2~6个变化所对应的速度值测量见表2。
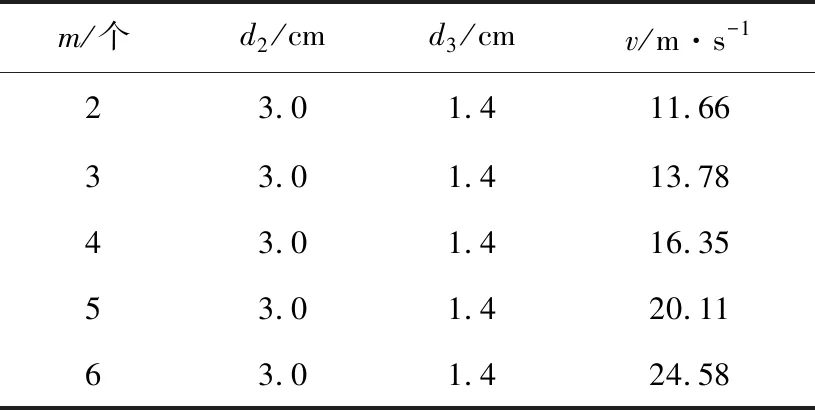
表2 矩形齿个数变化对应的速度
由表2可知,粉尘颗粒的运动速度随着矩形齿个数的增加而增加,获取康达管在矩形齿厚度为1.4 cm,纵向长度为3.0 cm时,不同矩形齿个数时的速度云图,在Planes里创建yz面查看,如图6所示。由图6可知,在不同的结构组合时,粉尘的运动速度是截然不同的,对于现有装置而言,改进的康达管对粉尘颗粒的运动速度大大提升。同时由速度云图可知,粉尘颗粒在管壁附近时,运动速度较低;在管内通道中间区域时,运动速度较高。原因是粉尘颗粒高速通过管道时,撞击管壁导致运动速度降低,造成管道中间速度高,管壁附近速度低的现象。由于粉尘颗粒的电荷量可由粉尘颗粒之间或粉尘颗粒与管壁的撞击来提升,所以不能仅以粉尘颗粒运动速度来判断静电感应量,还与管道的结构等参数有关。

图6 不同结构时的速度云图Fig. 6 Velocity cloud maps with different structures
3 静电感应量
感应电荷量计算式为
(1)
F(x,θ)=[(0.5d)2+x2-dxcosθ]1/2,
(2)
式中:z——颗粒速度v与时间t的乘积;
b——极板宽度;
q——以一定速度通过极板的点电荷;
d——环形极板的直径;
Q——极板上的感应电荷量;
x——感应电荷与极板中轴线的距离;
θ——积分块与轴线的夹角;
F——点电荷极点间的作用力[23]。
静电传感器数学模型各参数如图7所示。
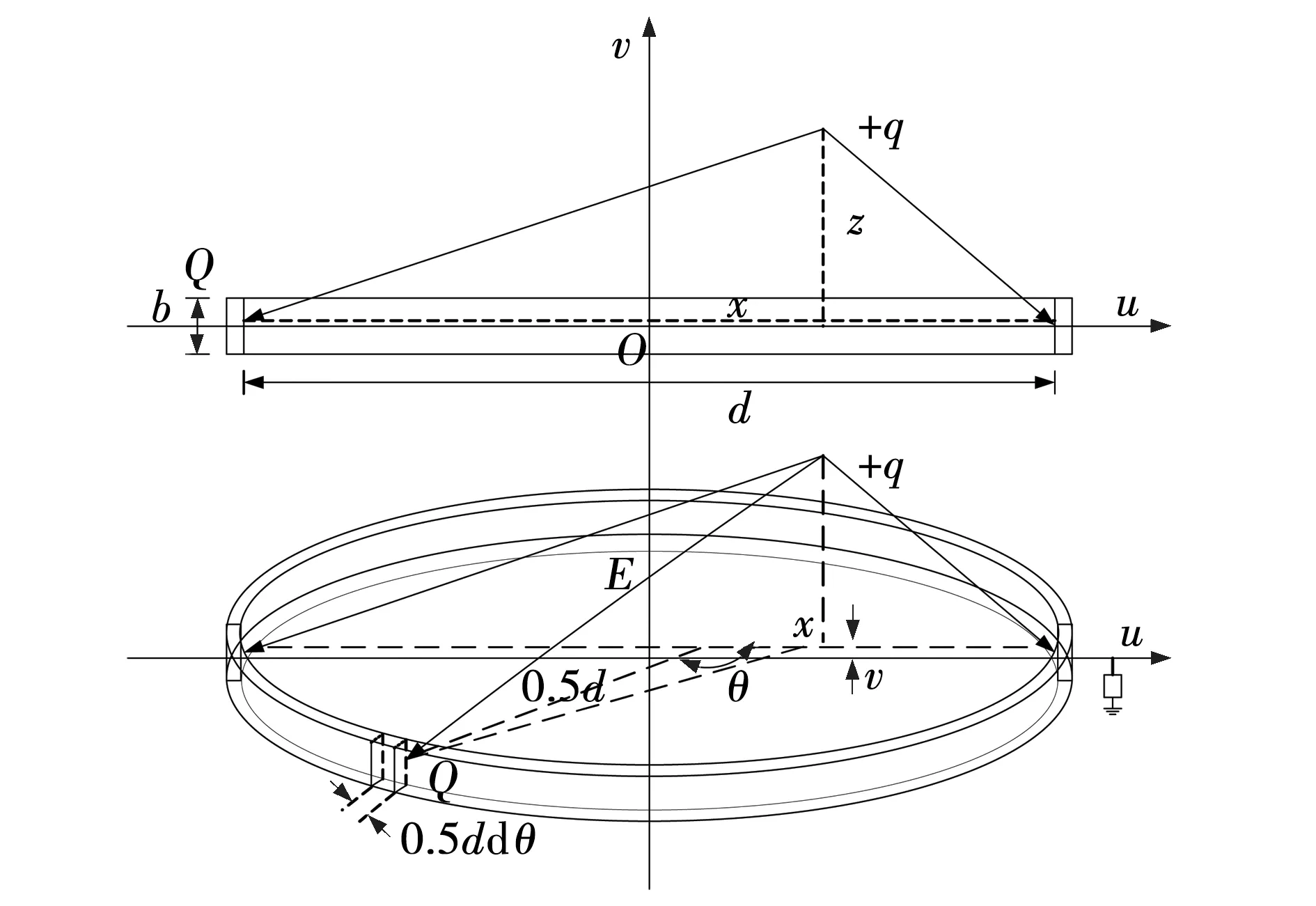
图7 静电传感器数学模型Fig. 7 Mathematical model of electrostatic sensor
由表2中的速度值,根据式(1)、(2)运用Matlab计算改进后康达管的电荷感应量,其电荷感应量归一化如图8所示。

图8 d2=3.0 cm、d3=1.4 cm时对应的速度值Fig. 8 Corresponding velocity values of d2=3.0 cm,d3=1.4 cm
由图8可以看出,粉尘颗粒粒径为1 μm,当d2=3.0 cm、d3=1.4 cm、m=4时,颗粒静电感应量最大。在Planes里创建yz面,查看粒径在10 μm时直管管道、改进前康达管、改进后康达管的速度云图如图9所示。当d2=3.0 cm、d3=1.4 cm、m=4时压力云图如图10所示。

图9 粒径为10 μm不同管道时的速度云图Fig. 9 Velocity nephogram of different pipes with particle size of 10 μm

图10 d2=3.0 cm、d3=1.4 cm、m=4时压力云图Fig. 10 Pressure nephogram of d2=3.0 cm, d3=1.4 cm, m=4
通过实验仿真及计算分析d2=3.0 cm、d3=1.4 cm、m=4时的不同粒径的粉尘速度并对比现有装置直管、改进康达管粉尘速度数据,如表3所示。由表3可知,在所测量粉尘的粒径中,改进后的康达管的速度值比改进前康达管速度值明显提高,表明粉尘颗粒运动在改进后康达管中较剧烈,易发生碰撞挤压。
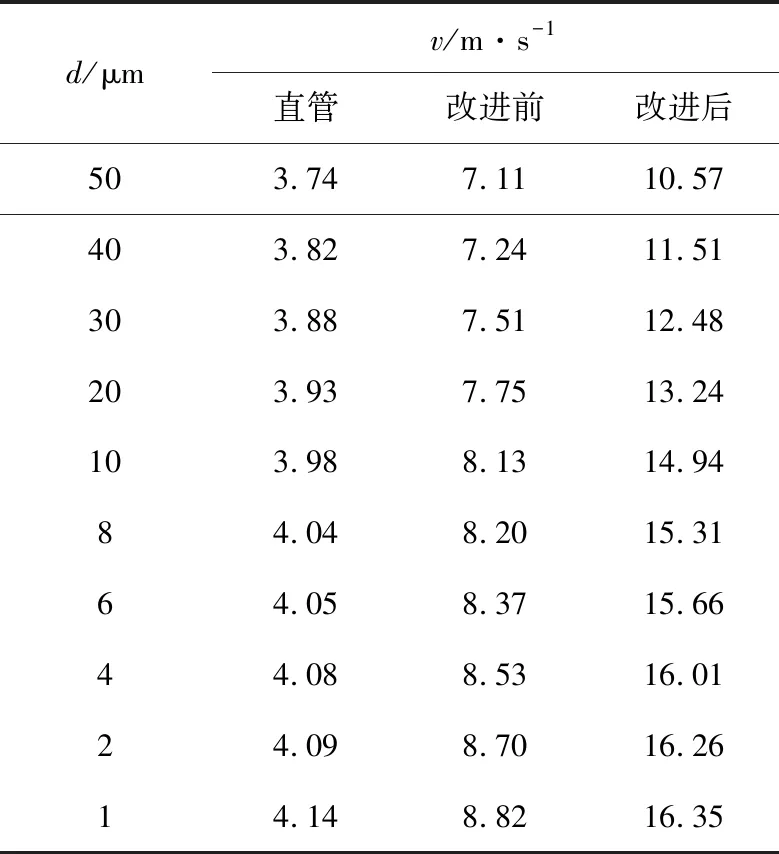
表3 不同管道的速度数据
从图10可以看出,改进后康达管的压力分布,管道压力在中间区域达到最大,也为粉尘运动速度在中间区域达到最大提供了验证依据。
由表3中的速度值,根据式(1)、(2),利用Matlab计算改进前康达管与改进后康达管,粒径不同时的电荷感应量归一化如图11所示。
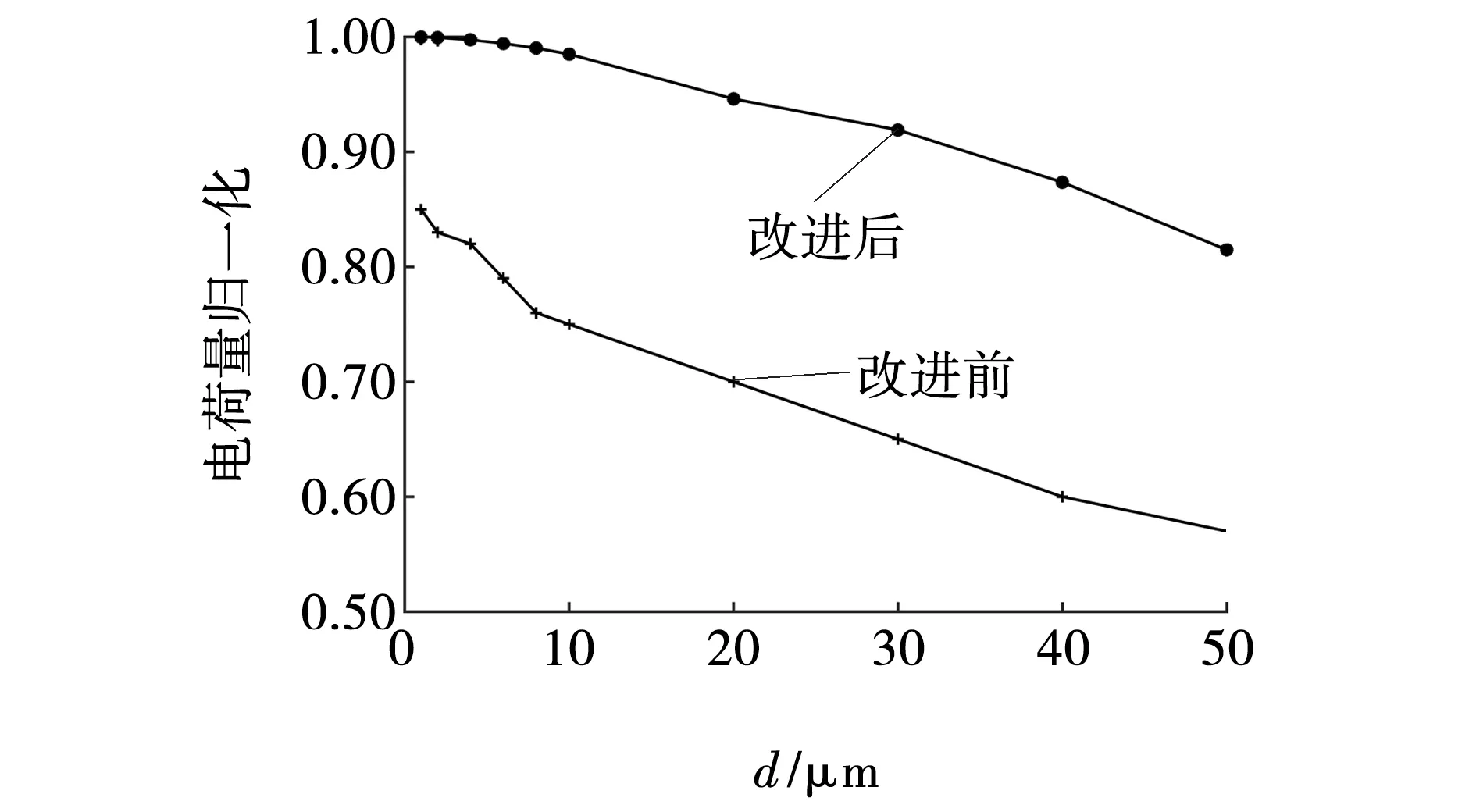
图11 粒径变化对应的电荷感应量对比Fig. 11 Comparison of charge inductance with particle
由图11可知,电荷量归一化曲线表明改进后康达管中粉尘所带感应电荷量大于改进前康达管的感应电荷量,由于改变了粉尘的运动速度,因此粉尘的静电感应量也会随之增加,由图11可见,粉尘感应电荷量明显增大,平均增加20.95%。由此可见,改进后的康达效应管道在速度的提升上更具优势。
4 结 论
(1)依据康达效应,通过分析现有装置结构,改进了康达效应管。采用ANSYS FLUENT,通过建立模型、仿真得到改进后康达管的各项速度值,在给定范围内寻得最优结构,当矩形齿结构纵向长度为3.0 cm、厚度1.4 cm、矩形齿个数为4时,粉尘颗粒电荷感应量最大。
(2)通过Matlab仿真分析静电感应量,粉尘颗粒在改进后装置的运动速度及静电感应量明显高于项目组先前研究的康达管,粉尘颗粒粒径越小,运动速度增幅越大。电荷感应量平均增加率为20.95%,颗粒粒径越小,电荷量增加率越大,对今后静电感应测量装置的改进提供参考。
(3)对项目组先前设计的康达管基础上增加了矩形齿结构,在有限范围内对改进后的康达管进行建模仿真,对康达管内部效应体勺型管与矩形齿结构的参数最优组合后续将作更加精确的研究。
