基于人工生态系统优化算法的组合生长需水预测模型

崔东文，包艳飞

(1.云南省文山州水务局，云南 文山 663000； 2.云南省水文水资源局曲靖分局，云南 曲靖 655000)

提高城市需水预测精度对城市建设规划和供水系统优化调度等具有重要意义。目前需水预测方法主要有人工神经网络法[1-5]、投影寻踪回归法[6]、马尔可夫链模型法[7]、随机森林法[8]、优选GM(0,N)模型法[9]、组合模型法[10-11]等。生长模型作为趋势外推法的一种重要方法，除用于描述和预测生物个体的生长发育以外，已在某些技术、经济特性等领域得到广泛应用[12]。常用的生长模型有Logistic模型、Richards模型、MMF模型、Hyperbola模型、Korf模型、Weibull模型、Gompertz模型、Usher模型等，已在人口预测[13]、林火预测[14]、地表沉降[15-17]、林分断面积研究[18]、油气田产量预测[19]、电能消费量预测[20]、径流预测[21]等行业领域得到应用，但在需水预测相关研究中应用较少。研究表明，制约生长模型应用的关键在于模型相关参数的合理确定，目前主要采用四点法、三段法、最小二乘法等进行参数估算，不但求解复杂，且效率不高。虽然遗传算法(GA)[22]、粒子群优化(PSO)算法[20,23-24]、果蝇优化算法(FOA)[25]、差分进化(DE)算法[26]已尝试用于Weibull模型、Gompertz模型、Richards模型、Usher模型参数的选取，具有较好的实际意义，但存在GA、PSO等传统智能算法收敛速度慢和易陷入局部极值、仅针对单一生长模型参数进行优化、所选用算法缺乏优化性能评估等问题。

为拓展需水预测模型及方法，进一步提高需水预测精度，本文选取Weibull、Richard、Usher 3种单一生长模型进行组合，构建Weibull-Richards-Usher、Weibull-Richards、Weibull-Usher、Richards-Usher 4种组合生长模型，提出基于人工生态系统优化(artificial ecosystem-based optimization，AEO)算法[27]的组合生长需水预测模型，利用AEO算法同时优化各组合生长模型参数和组合权重系数，构建不同组合需水预测模型，以上海市需水预测为例进行验证，旨在验证基于AEO算法的组合生长模型应用于城市需水预测的可行性和有效性。

1 基于AEO算法的组合生长模型

1.1 AEO算法

AEO算法是Zhao等[27]于2019年通过模拟地球生态系统中能量流动而提出一种新型元启发式优化算法，该算法通过生产算子、消费算子和分解算子对生态系统中的生产、消费和分解行为进行模拟来达到求解优化问题的目的。生产算子旨在加强AEO算法勘探和开发之间的平衡能力；消费算子用于改进AEO算法的探索能力；分解算子旨在提升AEO算法的开发性能。与传统群智能算法相比，AEO算法不但实现简单，除群体规模和最大迭代次数外，无需调整其他任何参数，且具有较好的寻优精度和全局搜索能力。

AEO算法遵行以下3个准则：①生态系统作为种群包括3种生物：生产者、消费者和分解者，且种群中分别只有一个个体作为生产者和分解者，其他个体作为消费者；②每个个体都具有相同的概率被选择为食肉动物、食草动物或杂食动物；③群体中每个个体的能量水平通过适应度值进行评价，适应度值按降序排序，适应度值越大表示最小化问题的能量水平越高。参考文献[27]，AEO算法数学描述简述如下：

a. 生产者。生态系统中，生产者可以利用CO2、水和阳光以及分解者提供的营养来产生食物能量。在AEO算法中，种群中的生产者(最差个体)通过搜索空间上下限和分解者(最优个体)进行更新，更新后的个体将引导种群中的其他个体搜索不同的区域。模拟生产者行为的数学模型如下：

x1，t+1=[1-(1-t/T)r1]xn+(1-t/T)r1xrand，t

(1)

其中

xrand=r(U-L)+L

式中:x1为生产者个体空间位置；xn为当前群体中最佳个体空间位置；n为种群规模；T为最大迭代次数；t为当前迭代次数；xrand为搜索空间中随机生成的个体空间位置；U、L分别为空间上、下限；r、r1为[0,1]之间的随机数。

b. 消费者。生产者提供食物能量后，每个消费者均可随机选择能量水平较低的消费者或生产者或两者兼有获得食物能量。如果消费者被随机选择为食草动物，它只以生产者为食；如果消费者被随机选择为食肉动物，它只能随机选择能量水平较高的消费者为食；如果消费者被随机选择为杂食动物，它可以同时选择能量水平较高的消费者和生产者为食。模拟食草动物、食肉动物、杂食动物消费行为的数学模型分别为

xi,t+1=xi,t+Cxi，t-x1，t(i=2,3,…,n)

(2)

(3)

(4)

其中C=0.5v1/|v2|v1～N(0,1)v2～N(0,1)

式中：xi为第i个消费者个体空间位置；C为具有levy飞行特性的消费因子；N(0,1)为呈正态分布、均值为0、标准差为1的概率密度函数；xj为具有较高能量水平的消费者和生产者；r2为[0,1]范围内的随机数。

c. 分解者。就生态系统功能而言，分解是一个非常重要的过程，它为生产者提供必要的养分。为提高算法的开发性能，AEO算法允许每个个体的下一个位置围绕最佳个体(分解者)传播，并通过调节分解因子D和权重系数e、h来更新群体中第i个消费者的空间位置。其模拟分解行为的数学模型为

xi,t+1=xn,t+D(exn,t-hxi,t) (i=1,2,…,n)

(5)

其中D=3uu～N(0,1)

e=r3randi(1,2)-1h=2r3-1

式中r3为[0,1]之间的随机数。

1.2 组合生长模型

a. Weibull模型。Weibull模型最早由瑞典工程师Waloddi Weibull于1951年提出并逐渐发展而来，目前已在油气田产量[19]、地基沉降[22]、泥石流预警[28]、药物溶出曲线评价[29]等领域得到应用。Weibull模型表述形式多样，本文利用式(6)所示函数模型进行需水预测。

(6)

b. Richards模型。Richards模型是描述生物生长的非线性回归方程，含有4个参数，目前已在碳排放量预测[30]、人口预测[13]、地表沉降[15]等领域得到应用。Richards模型表述形式多样，本文利用式(7)所示函数模型进行需水预测。

(7)

式中：W′2为Richards模型需水预测值；a、b、co、d为待优化参数。

c. Usher模型。Usher模型最早由美国学者Usher于1980年提出用于描述增长信息随时间变化的数学模型，目前已在围岩变形预测[21]、油田开发[31]、沉降预测[22,32]等领域得到应用。Usher模型表述形式多样，本文利用式(8)所示函数模型进行需水预测。

(8)

式中：W′3为Usher模型需水预测值；A、B、Co、D为待优化参数。

利用AEO算法对Weibull-Richards-Usher、Weibull-Richards、Weibull-Usher、Richards-Usher模型参数和权重系数进行优化，得到待优化的4种组合生长模型：

W′W-R-U=ωWW′1+ωRW′2+(1-ωW-ωR)W′3

(9)

W′W-R=ωWW′1+(1-ωW)W′2

(10)

W′W-U=ωWW′1+(1-ωW)W′3

(11)

W′R-U=ωRW′2+(1-ωR)W′3

(12)

式中：W′W-R-U、W′W-R、W′W-U、W′R-U分别为Weibull-Richards-Usher、Weibull-Richards、Weibull-Usher、Richards-Usher组合生长模型需水预测值；ωW、ωR分别为Weibull、Richards模型权重系数。

1.3 仿真验证

本文实例优化维度有3维、9维、10维、20维、21维、31维和118维，为验证AEO算法在不同维度条件下的寻优能力，选取Sphere、Schwefel 2.22、Schwefel 1.2、Griewank、Rastrigin、Ackley 6个典型测试函数在5维、10维、20维30维和100维条件下对AEO算法进行仿真验证，并与当前寻优能力较好的WOA、GWO、TLBO算法和传统PSO算法的仿真结果进行比较。上述6个函数变量取值范围分别为[-100,100]、[-10,10]、[-100,100]、[-600,600]、[-5.12,5.12]、[-32,32]，理论最优解值均为0。其中，函数Sphere、Schwefel 2.22、Schwefel 1.2为单峰函数，主要用于测试算法的寻优精度；函数Griewank、Rastrigin、Ackley为多峰函数，主要用于测试算法的全局搜索能力。基于Matlab 2018 a M语言实现5种算法对6个标准测试函数的20次寻优，利用平均值对5种算法寻优性能进行评估，见表1。试验参数设置如下：AEO、WOA、GWO、TLBO、PSO 5种算法最大迭代次数T=1 000，种群规模n=50。其中，WOA对数螺旋形状常数b=2；TLBO算法参数TF为1～10之间随机整数；PSO算法惯性权重wmax、wmin分别取值0.9和0.6，自我学习因子、社会学习因子c1、c2均取值2.0。其他参数采用各算法默认值。

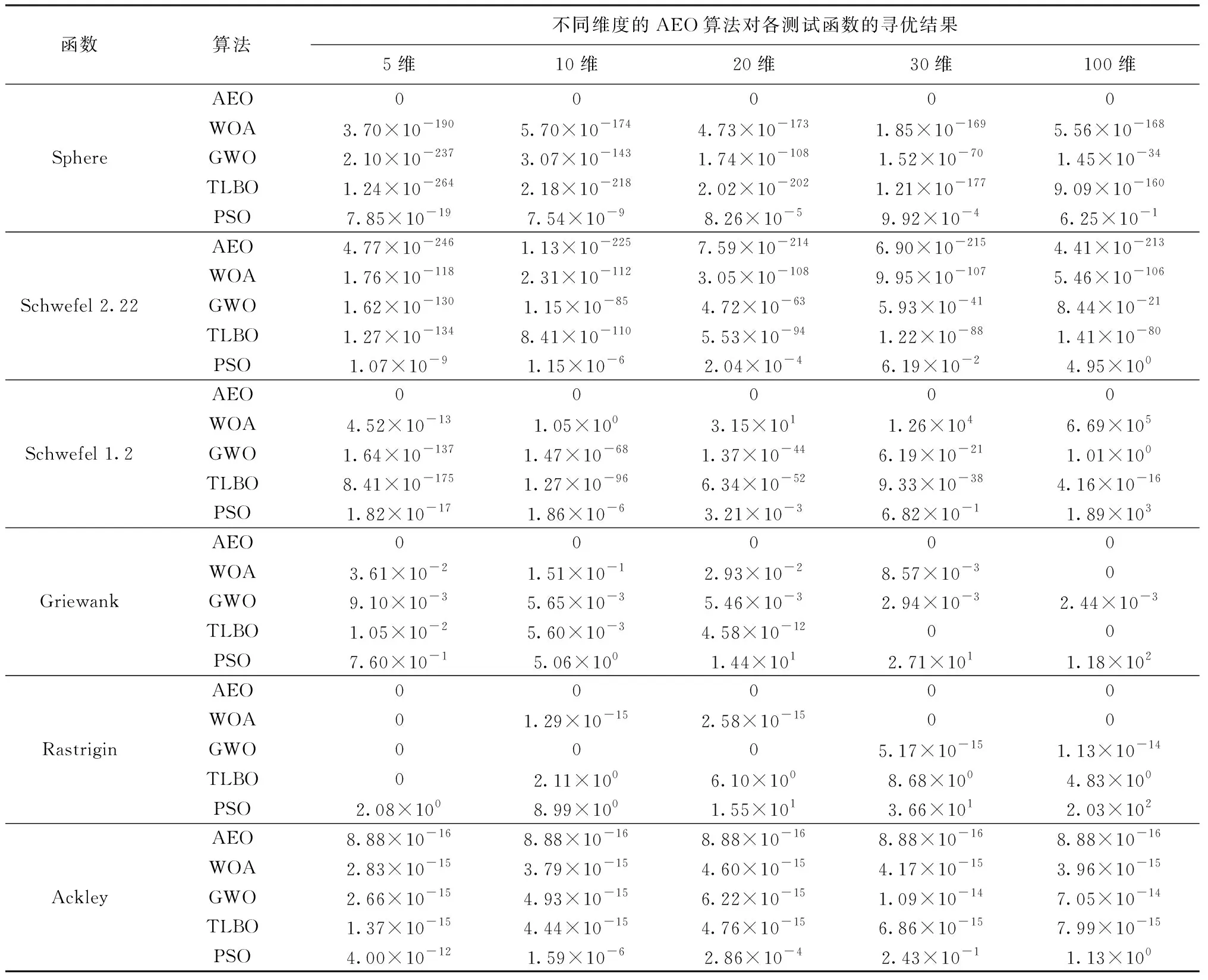
表1 函数优化对比结果Table 1 Comparison results of function optimization

对于单峰函数Sphere，AEO算法在不同维度条件下20次寻优均获得理论最优值0，寻优精度优于WOA、TLBO、GWO算法，远优于PSO算法；对于具有明显转折点的非线性函数Schwefel 2.22，AEO算法在不同维度条件下寻优精度较其他4种算法提高100个数量级以上，具有较好的寻优精度；对于倒锥形非线性函数Schwefel 1.2，AEO算法在不同维度条件下20次寻优均获得理论最优值0，寻优精度优于TLBO、GWO算法，远优于WOA、PSO算法。对于上述单峰函数，AEO算法寻优效果基本不受维变化的影响，而随着维度的增加，WOA、TLBO、GWO、PSO算法寻优精度下降显著。

对于典型多峰多模态函数Griewank，AEO算法在不同维度条件下20次寻优均获得了理论最优值0，低维条件下(5维、10维)寻优精度远优于WOA、TLBO、GWO和PSO算法。随着维度的增加，TLBO、WOA算法寻优精度不降反升；对于典型易陷入局部极值多峰函数Rastrigin，AEO算法20次寻优获得理论最优值0，寻优精度优于10维、20维条件下的WOA和高维(30维和100维)条件下的GWO算法，远优于不同维条件下的PSO算法和10维、20维、30维和100维条件下的TLBO算法；对于连续旋转不可分多峰函数Ackley，AEO算法在不同维度条件下20次寻优均获得相对理论最优值8.88×10-16，寻优精度优于WOA、TLBO、GWO算法，远优于PSO算法。对于上述多峰函数，AEO算法寻优效果不受维变化的影响。

可见，AEO算法在5维、10维、20维、30维和100维条件下对上述6个标准测试函数均获得理想的寻优效果，寻优精度优于WOA、TLBO、GWO算法，远优于PSO算法，且寻优精度基本不受维度变化的影响，具有较好的寻优精度和全局搜索能力。

1.4 组合生长模型预测实现步骤

步骤1：选取需水预测影响因子，构造上述4种需水预测组合生长模型的输入、输出向量，合理划分训练样本和预测样本，利用式(13)对实例数据序列进行归一化处理；设定组合生长模型参数和权重系数搜寻范围。

(13)

式中：z′为经过归一化处理的数据；z为原始数据；zmax和zmin分别为序列中的最大值和最小值。

步骤2：确定组合生长模型适应度函数。本文选用训练样本均方误差作为适应度函数，描述如下：

(14)

(15)

(16)

(17)

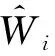
步骤3：设置AEO算法种群规模n、最大迭代次数T和算法终止条件；随机初始化生态系统xi，计算适应度值，保留当前最佳个体空间位置xbest。令当前迭代次数t=0。

步骤4：利用式(1)更新生产者空间位置。

步骤5：在[0,1]之间生成随机数r，若r<1/3，利用式(2)更新消费者个体空间位置；若1/3≤r≤2/3，利用式(3)更新消费者个体空间位置；其他利用式(4)更新消费者个体空间位置。计算每个个体空间位置适应度值，找到并保留当前最佳个体空间位置xbest。

步骤6：利用式(5)更新分解过程中消费者个体空间位置，计算每个个体适应度值，找到并保留当前最佳个体空间位置xbest。

步骤7：比较并保存最佳个体空间位置，即算法最优解xbest。

步骤8：令t=t+1。判断算法是否达到终止条件，若是，输出全局最优解xbest，算法结束；否则重复步骤4～8。

步骤9：输出最优适应度值及全局最优位置xbest，xbest即为各组合生长模型参数和权重系数向量。将参数xbest代入各组合生长模型进行需水预测。

2 实例应用

2.1 数据来源

在充分考虑需水预测影响因子和指标获取难易程度的基础上，依据2018年上海统计年鉴，以1980—2017年为时间系列，选取7个指标作为上海市需水预测的影响因子：z1为第一产业总产值、z2为第二产业总产值、z3为第三产业总产值、z4为户籍人口、z5为农业总产值、z6为工业总产、z7为建筑业总产值。利用SPSS软件分析此7个影响因子与需水量的相关系数分别为0.984、0.906、0.798、0.940、0.988、0.890、0.830。利用1980—2009年统计数据作为训练样本，2010—2017年作为预测样本。

2.2 参数设置

设置4种组合生长模型参数的搜索范围为[0,10]，Weibull、Richards模型权重系数搜索范围见式(14)～(17)；Weibull、Richards、Usher单一模型对应的参数搜索范围同组合模型；SVM模型惩罚因子P、核函数参数g、不敏感系数ε搜索范围均为[2-5,25]，交叉验证折数V=3；BP网络结构为7-13-1，隐含层和输出层传递函数均分别采用logsig和purelin，训练函数采用trainlm，设定期望误差为0.001,最大训练轮回为100次，搜索空间为[-1,1]。AEO算法参数设置同上；SVM、BP模型采用[0.1,0.9]对原始数据进行归一化处理。

2.3 模型构建及预测

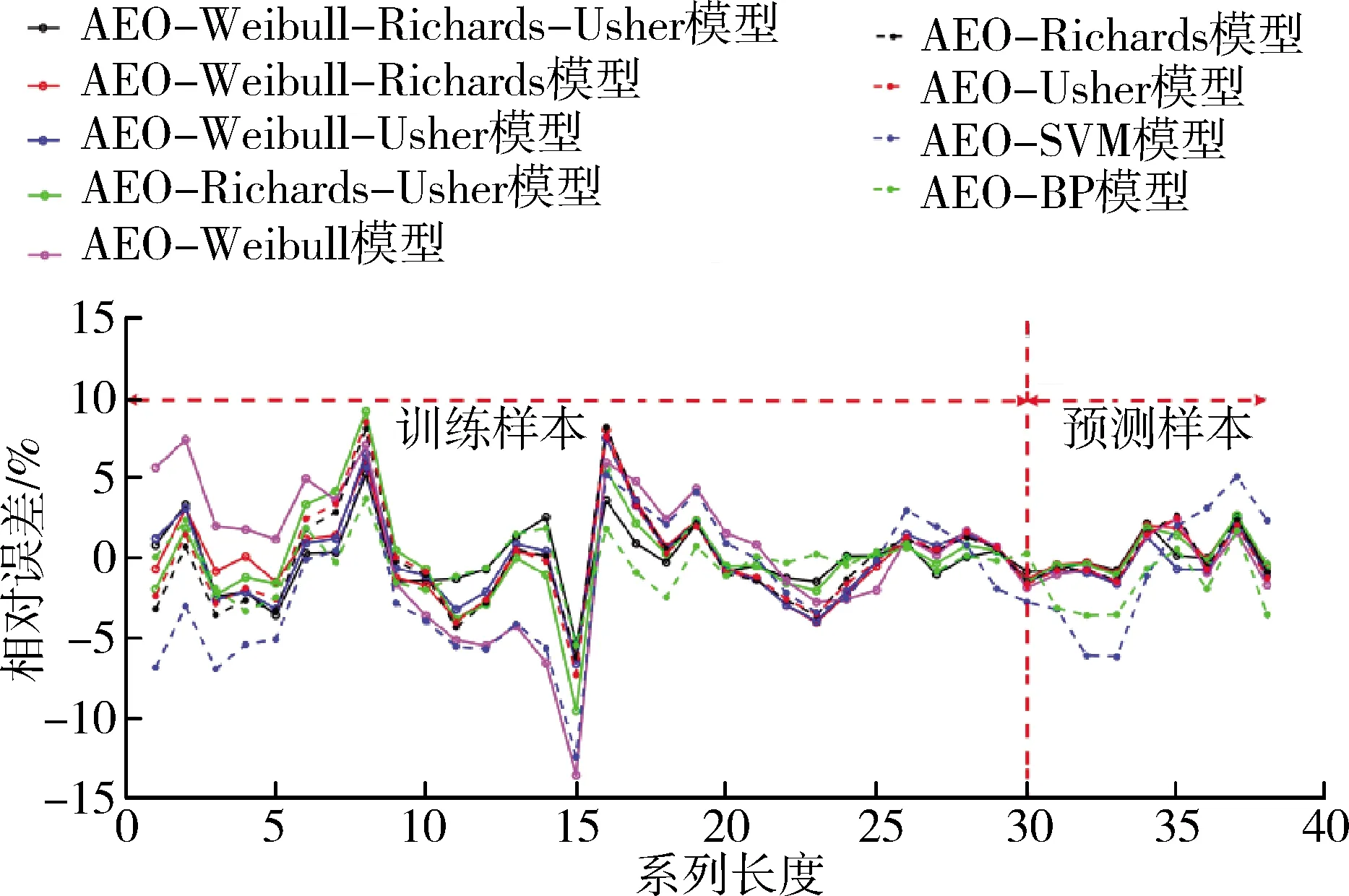
分别构建AEO-Weibull-Richards-Usher、AEO-Weibull-Richards、AEO-Weibull-Usher、AEO-Richards-Usher、AEO-Weibull、AEO-Richards、AEO-Usher、AEO-SVM、AEO-BP模型对实例需水量进行训练及预测。选取平均相对误差绝对值REM、平均绝对误差AEM、最大相对误差绝对值REMax和适应度值minW作为评价指标，利用此9种模型对实例需水进行预测，结果见表2，并给出9种模型不同系列长度的训练、预测阶段的相对误差和绝对误差结果见图1。

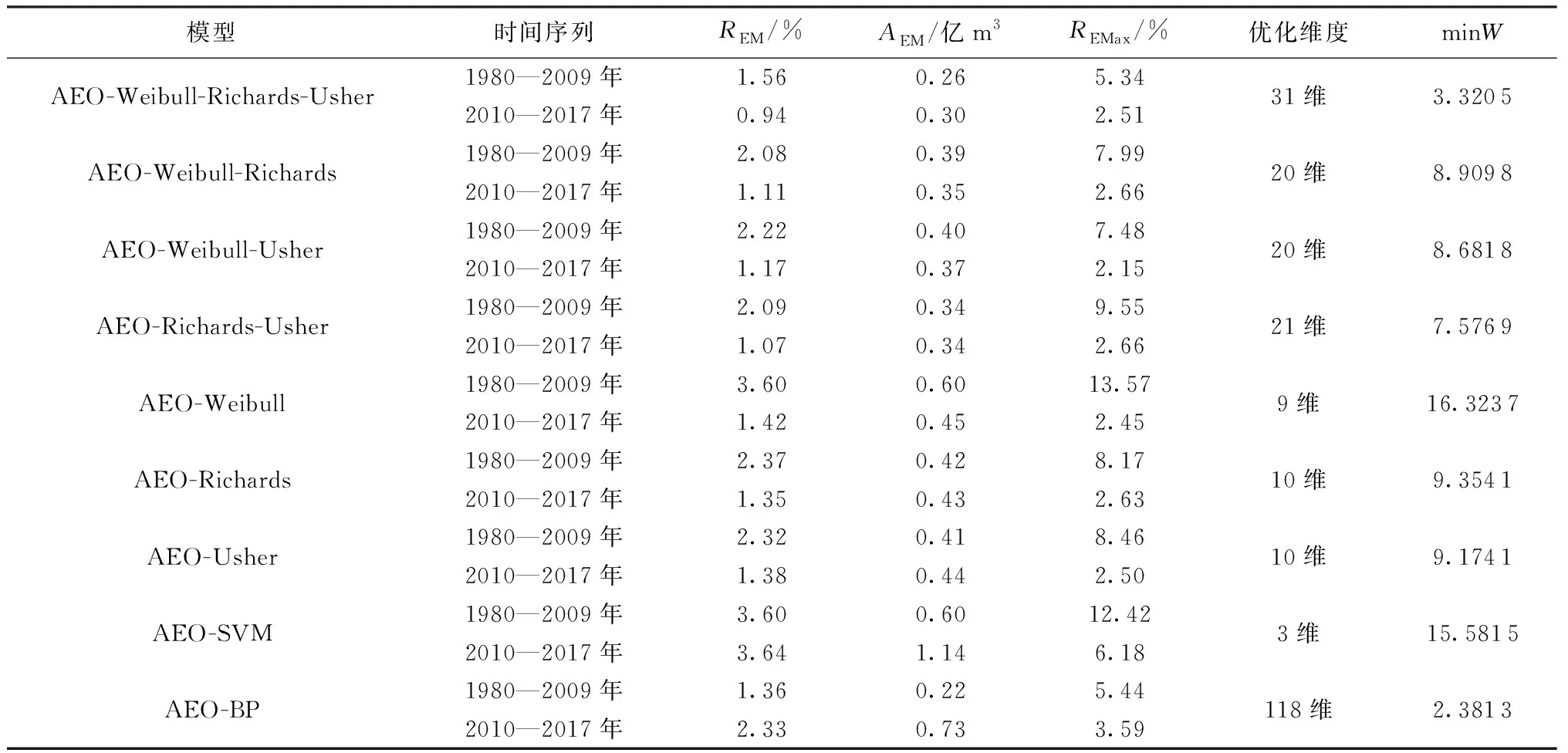
表2 需水预测各模型测结果Table 2 Test results of various models for water demand prediction

由表2及图1可见，4种组合生长模型对实例训练样本拟合的REM、AEM分别在1.56%～2.22%、0.26亿～0.40亿m3之间，拟合精度均优于3种单一生长模型和AEO-SVM模型；对实例预测样本的REM、AEM分别在0.94%～1.17%、0.30亿～0.37亿m3之间，尤以AEO-Weibull-Richards-Usher模型预测精度最高，其REM、AEM分别达到了0.94%和0.30亿m3，4种组合生长模型预测精度均优于AEO-Weibull、AEO-Richards、AEO-Usher、AEO-SVM、AEO-BP模型，具有较好的预测精度和泛化能力，表明Weibull、Richards、Usher模型间具有互补性，AEO算法能同时有效优化各组合生长模型参数和权重系数，基于AEO算法的组合生长模型用于需水预测是可行和有效的。

(a) 相对误差

(b) 绝对误差图1 9种模型不同系列长度的训练、预测阶段的相对误差和绝对误差Fig.1 Relative error and absolute error results of training and prediction stages of 9 models with different series lengths

从各组合生长模型参数和权重系数优化结果来看，对于AEO-Weibull-Richards-Usher模型，Usher权重系数为0.424 2，大于0.33，表明Usher占主导地位；对于AEO-Weibull-Richards模型，Weibull权重系数0.955 9，大于0.5，表明Weibull占绝对主导地位；对于AEO-Weibull-Usher模型，Usher权重系数0.679 3，大于0.5，表明Usher占主导地位；对于AEO-Richards-Usher模型，Usher权重系数0.836 1，大于0.5，表明Usher占主导地位。3种含有Usher的组合模型中，Usher模型均占主导地位，表明Usher模型对该实例具有较好的拟合-预测效果(从AEO-Usher模型的拟合、预测结果亦可看出)。

AEO-Weibull、AEO-Richards、AEO-Usher 3种单一生长模型的预测效果在伯仲之间，其对实例2010—2017年需水预测的REM、AEM分别在1.35%～1.42%、0.43亿～0.45亿m3之间，预测精度优于AEO-SVM、AEO-BP模型，表明单一生长模型在需水预测中同样具有较好的预测效果，其关键之处在于合理选取模型的相关参数。相对而言，AEO-Weibull模型拟合效果劣于AEO-Richards、AEO-Usher模型。

从AEO-SVM、AEO-BP模型拟合、预测结果来看，AEO-SVM模型拟合、预测精度均不佳，存在“欠拟合”现象；AEO-BP模型拟合精度较好，但预测效果较差，存在“过拟合”现象。经笔者反复调试，AEO-SVM、AEO-BP模型均不能获得较好的预测效果，原因在于输入向量，即7个需水预测影响因子均随时间呈逐年增加趋势，影响因子间相关性较好，存在多重共线性问题。

本实例虽然采用AEO算法对BP、SVM模型关键参数进行优化，具有一定的智能化水平，但BP模型的隐层节点数、隐含层和输出层传递函数、期望误差等参数均需人为设定，在一定程度上影响了模型的预测精度；SVM模型的交叉验证折数V需人为设定，V值过大或过小均会导致模型出现“过拟合”或“欠拟合”现象，从而影响AEO-SVM模型的预测效果。本文提出的AEO-Weibull-Richards-Usher、AEO-Weibull-Richards、AEO-Weibull-Usher、AEO-Richards-Usher组合生长模型所有参数和权重系数均由AEO算法优化获得，无须人为设定，具有较高的智能化水平和较好的实际应用价值。

3 结 论

a. 在不同维度条件下，AEO算法寻优精度优于WOA、GWO、TLBO算法，远优于PSO算法，具有较好的寻优精度和全局搜索能力。

b. 4种组合生长模型的预测精度均优于AEO-Weibull等5种模型，表明Weibull、Richards、Usher模型间具有互补性，AEO算法能同时有效优化各组合生长模型参数和权重系数，基于AEO算法的组合生长模型用于需水预测是可行和有效的，组合生长模型具有较好的预测精度和泛化能力，模型及方法可为需水预测及其他相关预测研究提供新的途径和方法。

c. 解决了各组合模型及Weibull、Richards、Usher单一生长模型参数选取困难的实际问题，各组合生长模型权重系数由AEO算法优化获得，无需人为计算或设定，具有较高的智能化水平和较好的实际应用价值。