LID径流控制效果对设计暴雨重现期的响应

杨少雄,侯精明,陈光照,李东来,马 越,梁行行

(1.西安理工大学西北旱区生态水利国家重点实验室，陕西 西安 710048；2.陕西省西咸新区沣西新城开发建设(集团)有限公司海绵城市技术中心，陕西 西安 712000)

为了有效解决气候变化和城市化进程加快[1]导致的城市内涝频发[2-3]的问题，美国于20世纪90年代提出低影响开发(low impact development, LID)[4]。2009年，仇保兴[5]提出在城市规划时推广LID，以达到不改变地表径流量、减少对环境影响的目的。随着海绵城市建设的兴起，海绵城市建设效果的评估成为国内各界关注的热点[6-7]。1971年美国环境保护署开发出SWMM模型，Colston[8]利用SWMM模型对城市径流的特征进行了模拟，SWMM模型在新版本中加入了LID模块；2007年，侯爱中等[9]利用SWMM模型对国内下凹式绿地和蓄水池两种海绵措施对城市型洪水的影响进行了研究；2014年，Marléne等[10]以悉尼西部某城市为研究区域，根据SWMM模型对该区域的模拟结果进行分析，得到雨水滞留池可以减少洪峰流量与系统径流量的结论。但以上研究只是对单一LID措施的径流控制效果进行模拟，而对系统的LID措施对径流控制效果未进行分析。2017年，侯精明等[11]利用自主开发的基于GPU加速技术的耦合水文水动力过程的二维城市雨洪模型，研究了不同设计暴雨雨型对城市内涝的影响，发现设计暴雨重现期短于20 a时，峰值比例较小的设计暴雨内涝积水总量较大，而重现期长于20 a时，规律相反，系统地揭示了暴雨雨型与内涝积水的量化规律，但作者未对径流控制率变化的量化规律进行系统研究；2018年，张曼等[12]基于SWMM模型对城市典型LID措施水文效应及雨洪控制效果进行基础性的模拟研究，得到LID措施的不同组合对径流控制效果的影响，但未对已建成海绵小区不同重现期的径流控制效果进行模拟；2016年，Laurent等[13]通过研究发现LID措施对城市洪水有明显削减作用，但并未对不同重现期的降雨对径流的影响进行研究；陈莎等[14]基于SWMM模型对海绵城市建设前后不同降雨条件径流削减效果进行数值模拟，发现海绵城市建设后对径流削减效果显著；朱寒松等[15]基于SWMM模型对城市工业园区LID效果进行了模拟评估，得到LID措施的径流削减效果在重现期为2 a、10 a时更显著的结论，但未对较大降雨重现期的径流控制效果以及量化规律进行模拟研究；刘家宏等[16]基于海绵城市建设技术指南核算了特定年份径流总量控制率，探讨了海绵城市不同水文年型径流总量控制率的量化规律。

上述研究对LID措施布设完成区域的场次降雨径流控制率随不同重现期量化规律进行的研究较少，但该量化规律对海绵城市建设区域进行内涝防治以及对海绵设施功能精确评估有重要意义。在自然条件下，由于城市区域降雨随机性显著，量化大重现期场次降雨条件下LID设施的径流控制效果，对揭示LID设施在极端降雨条件下的控制效果有重要意义。使用SWMM模型计算径流控制率，尤其是在较大重现期条件下，当管网产生溢流时，由于其对地表的简化，管网汇流部仅能模拟出管网节点的溢流量，却不能模拟出水体从节点溢流后在地表的淹没情况，无法精确计算当管网排水能力恢复后地表积水进入管网的水量[17-18]。本文基于GPU加速技术并耦合管网系统的高效高精度二维城市雨洪过程模型[19]，对西咸新区沣西新城某典型海绵建设小区在不同降雨重现期下径流控制率的变化规律进行模拟，以期对海绵城市LID建设效果评估提供理论依据。

1 数学模型及其求解方法

1.1 控制方程

模型地表产汇流部分采用考虑水文过程的二维水动力浅水方程(简称SWEs)[20]，守恒性方程为

(1)

式中:t为时间；h为水深；qx和qy分别为x、y方向上的单宽流量；u、v分别为x、y方向上的流速；f和g分别为x、y方向上的通量矢量；S为源项矢量；i为降雨强度；zb为底面高程；谢才系数Cf=gn2/h1/3,n为曼宁系数；g为重力加速度。

地表水汇入雨水井的水量计算采用堰流公式：

(2)

式中：Q为地表水汇入管网的流量；m为流量系数；b为雨水井宽度。经过实际降雨与流量监测数据的验证，证明在研究区域内该公式具有良好的适用性。

管网模块采用扩散波方程计算管道流量，扩散波方程为

(3)

式中：A为管道过水断面面积；QT为管道流量；x为固定横截面沿流程的距离；dη/dx为水力坡降；Sf为摩阻比降。

1.2 求解方法

在求解地表产汇流模块时，采用Godunov格式有限体积法离散SWEs方程，采用二阶MUSCL方法对变量值进行空间插值来提高计算精度[21]。在控制单元内，界面上的物质与动量通量通过HLLC近似黎曼求解器进行求解。通过二步龙格-库塔方法来进行时间推进。引入GPU加速技术，在不降低精度的条件下大幅提升计算速度[22]。在进行管网模块求解时，采用有限差分法对方程进行离散，将管道内的水流按照非恒定流形式进行计算，通过堰流公式计算地表雨水汇入雨水井的水量，通过求解扩散波方程计算管道流量，并且修正了雨水井出现负水深的情况，可以准确真实地反映排水系统的运行状态。

2 研究区域及基础数据

2.1 研究区域概况

陕西省西咸新区是国家第一批海绵试点城市之一。研究区域多年平均降水量约520 mm,其中5—10月降水量最多，7—9月降水量最大。夏季降水多以暴雨形式出现，易形成内涝。本文选取沣西新城天福和园小区为研究区域，小区位于沣西新城天府路以南，兴信路以西，咸户路以东，天雄西路以北(图1)[23]。研究区内布设有透水铺装和雨水花园两种LID措施，并安装有微气象站和流量监测仪器，监测数据完善。

图1 研究区域区位示意图Fig.1 Location map of study area

2.2 基础数据

2.2.1降雨数据

采用根据咸阳市秦都区国家基本气象站近30年(1981—2010年)的实测降雨资料分析得到的暴雨公式[24]为

(4)

式中：qi为设计暴雨强度；T为重现期；t为地面集水时间。利用暴雨公式和芝加哥雨型生成器得到不同重现期降雨，峰值比例为0.45，降雨时长为2 h，文中降雨雨强均为降雨时程的平均雨强。选取的降雨重现期为1 a、2 a、5 a、10 a、50 a和100 a，降雨过程线如图2所示。

图2 研究区域不同重现期降雨过程Fig.2 Rainfall processes of study area in different return periods

2.2.2地形及管网数据

本文所用DEM数据是通过无人机机载激光雷达技术获取的1 m高精度地形数据，高精度的地形能反映微观的地表特征，能精确体现小区内LID措施的调蓄作用，有效提高地表产汇流过程的准确性，研究区域地形见图3。

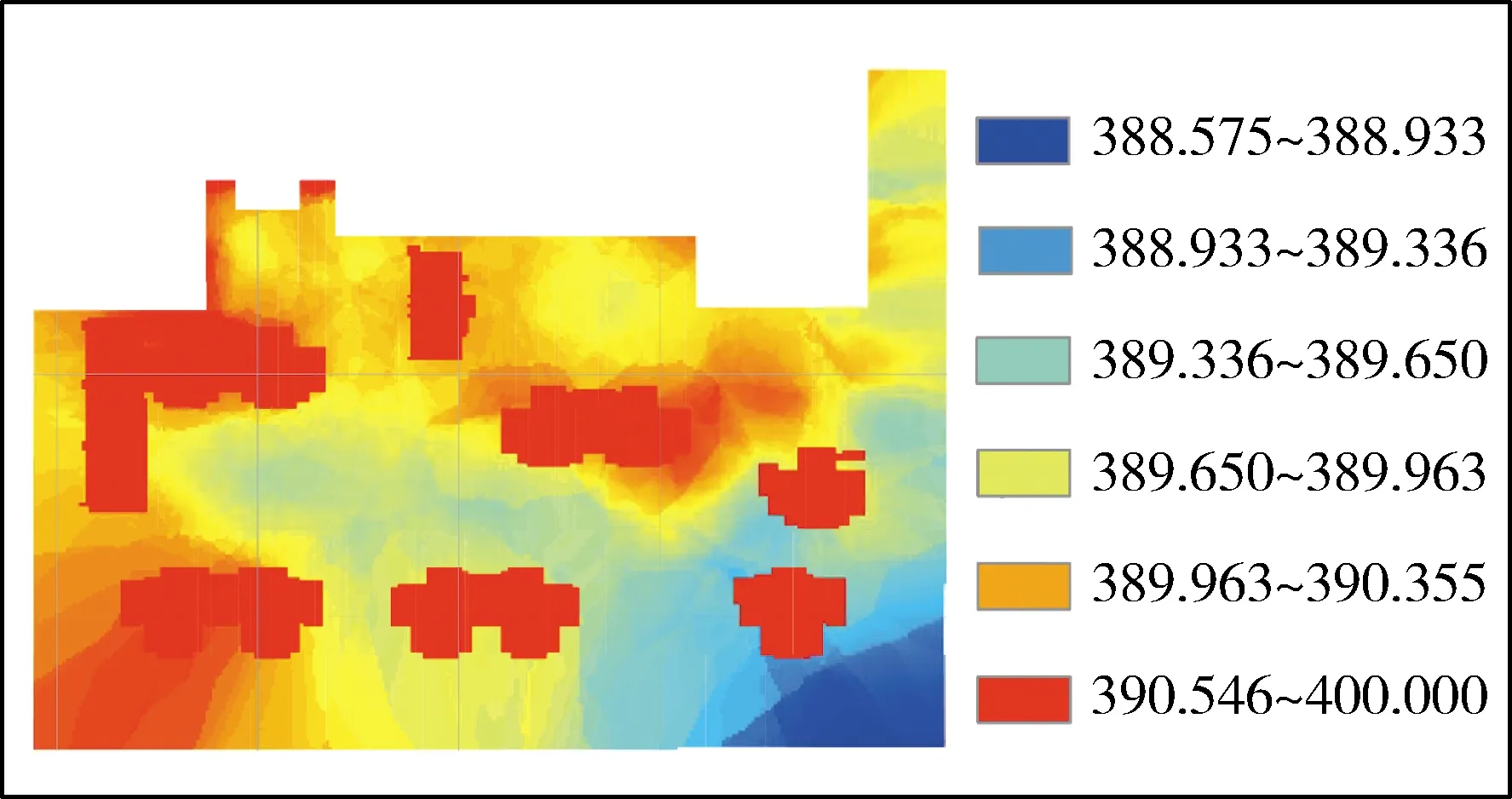
图3 研究区域高程(单位：m)Fig.3 DEM of study area(unit:m)

研究区域内主要的土地利用类型为LID设施、房屋、道路和绿地。小区内LID设施主要有雨水花园和透水铺装两种。土地利用类型分布如图4所示，下渗率根据双环进行实地测量。在模拟时，降雨强度大于绿地下渗率时，产生径流；而楼房在模拟时，考虑其高程，产生的径流由四周边界流入到相邻的区域。对于LID设施，当土地类型为透水铺装时，通过实验室实测透水铺装的下渗率来反映其相较于不透水道路的调蓄量；对于雨水花园，高精度地形可有效反映其调蓄深度与调蓄面积，下渗率为利用双环测渗仪现场原位测量值，可有效反映LID设施的调蓄量。在实际情况下，在雨水花园末端会有溢流口，溢流水量进入管网排出，处理时在有溢流口的雨水花园末端加管网节点。曼宁系数是径流过程的主要影响参数，通过模型验证发现，应用表中参数得到的西南排口流量过程的模拟结果与实测结果吻合较好，表明模型可用于典型LID设施小区径流过程的模拟。管网分布资料由沣西新城管委会提供，小区内管道为圆形，各管道半径为实际值，管道曼宁系数为0.013。管网排口位于小区西南角，外接市政管网，排口布设有流量计，用以监测排口出流流量过程。模型验证所应用的实测降雨来自天福和园内气象监测设备，流量数据来源于小区西南排口流量计。

图4 研究区域土地利用类型Fig.4 Land use type of study area

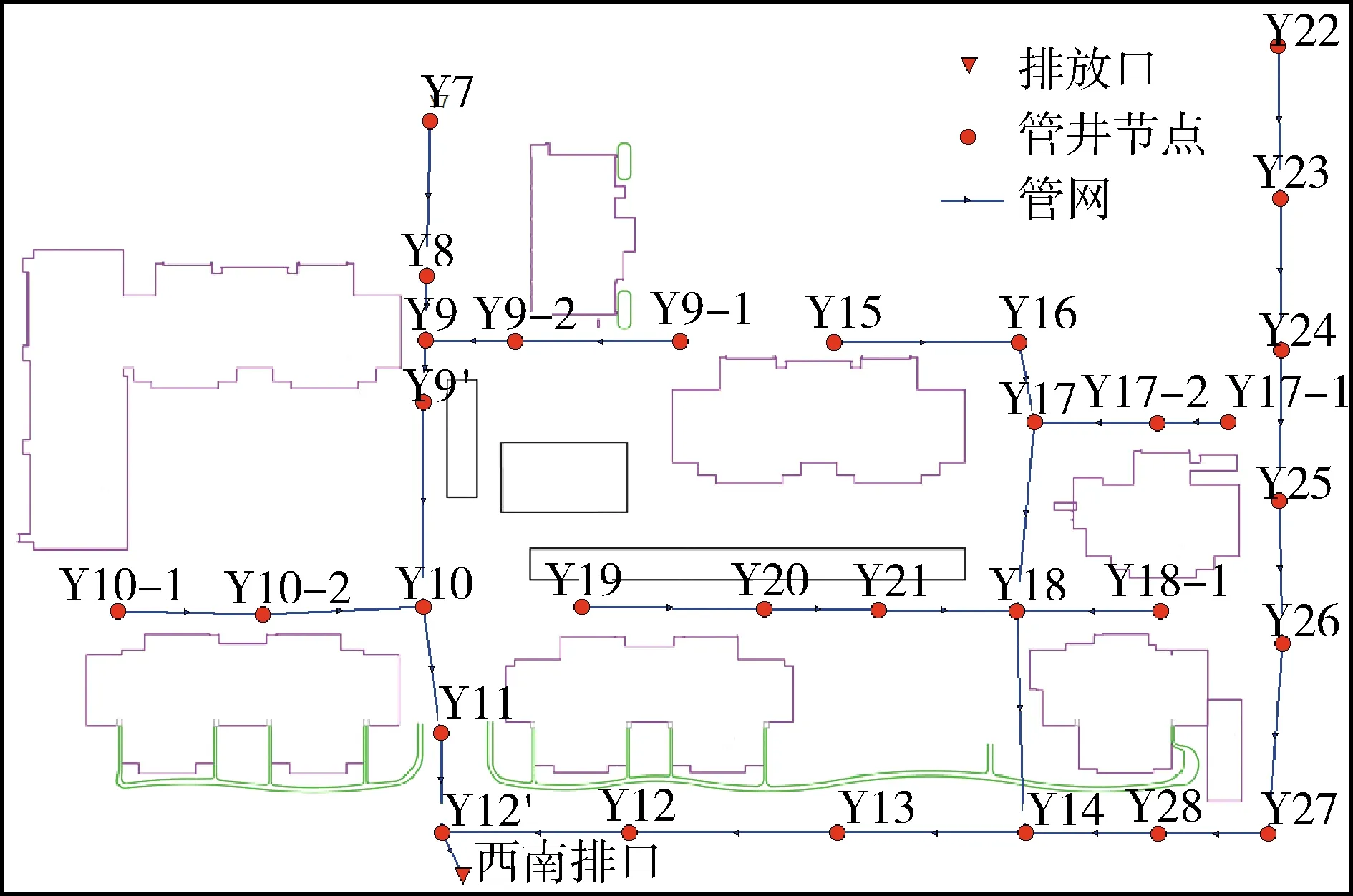
图5 研究区域管网布设Fig.5 Pipe network layout of study area

3 模型验证与结果分析

3.1 模型验证

根据文献[25-27]及实地测量选取下垫面相关参数，并利用天福和园2017年8月20日降雨对所建模型进行验证，模拟使用的参数见表1，得到结果见图6。由图6可知，本文所建模型模拟的结果与实测的流量过程吻合较好，证明本模型适用于典型LID建成区径流的模拟。

(a) 降雨过程

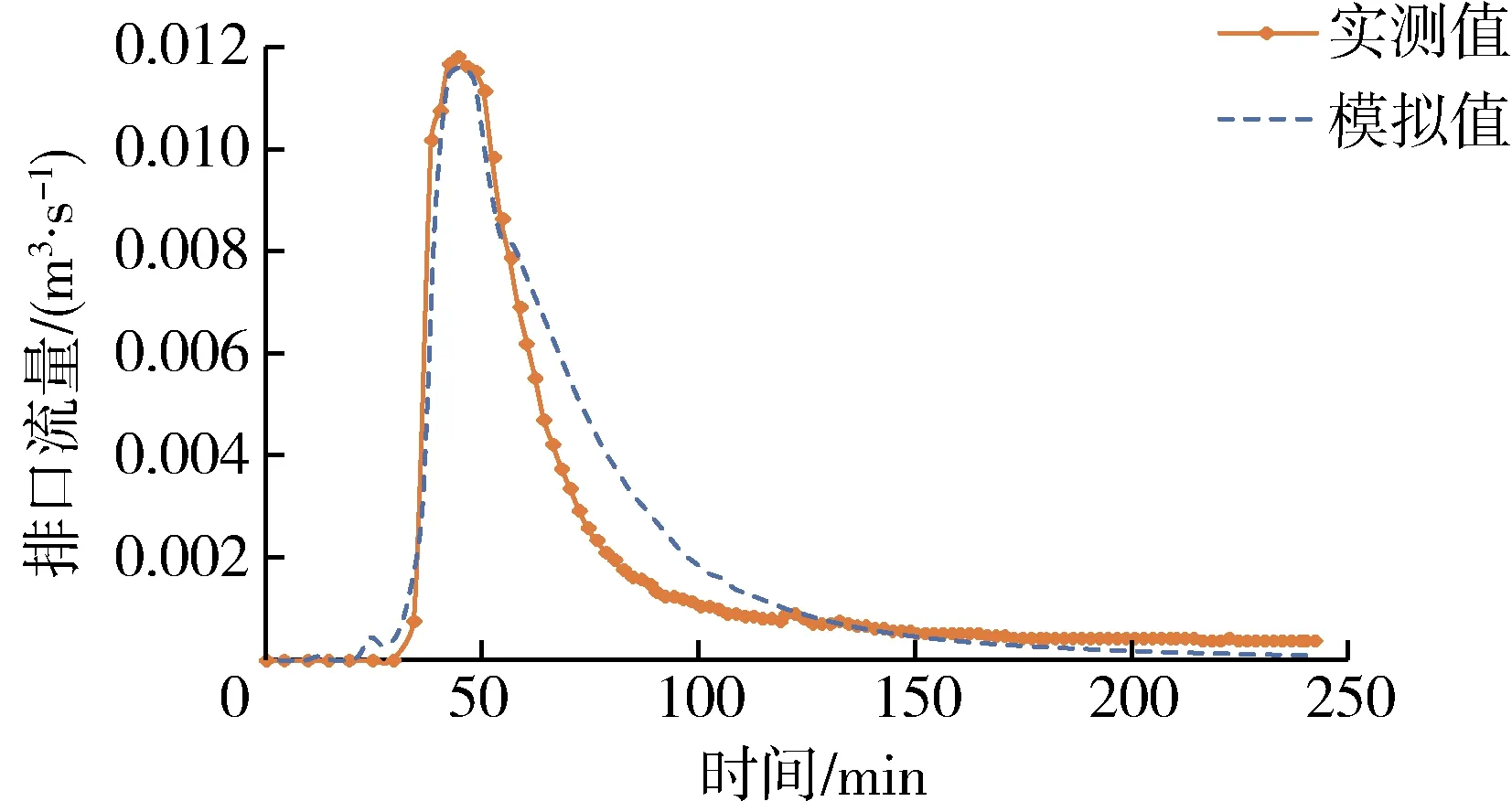
(b) 实测、模拟流量对比图6 8月20日降雨过程及实测、模拟流量对比Fig.6 Comparison of rainfall process and measured-simulated discharge on 20, August

表1 研究区域下垫面参数Table 1 Underlying surface parameters of study area

为了对率定结果进行定量化评价，引入纳什效率系数(Nash-Sutcliffe efficiency coefficient，NSE)作为模型率定和验证过程的评价标准，计算公式为

(5)

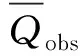
通过计算可得，2017年8月20日降雨NSE值为0.93，表明本文所用模型具有良好的适用性，所用参数合理。

3.2 模拟结果与分析

降雨径流控制率可通过统计、计算获取，计算公式为

(6)

式中:RAV为径流控制率；P为研究区总降水量；Vo为研究区对应降雨的外排总水量。

研究区为封闭区域，为研究径流控制率随降雨重现期的变化规律，在模拟时，利用耦合了管网模块的二维城市雨洪过程模型，输入地形、下垫面以及小区管网数据，模型模拟过程中采用闭边界，四周无入流，初始地表无积水，库朗数(CFL)设定为0.5。在模拟时，发现当降雨重现期为100 a且时长为2 h时，模拟时长到10 h左右，排口流量为1×10-6m3/s，故为了充分排空管网的水量，本文在模拟时选用模拟时长为12 h。当重现期较大管网产生溢流时，溢流出的水量进入地表计算，当管网具有排水能力时，再进入管网进行计算。对不同降雨重现期条件下的径流过程进行数值模拟，并根据模拟所得管网外排水量计算径流控制率，结果见表2。

表2 不同降雨重现期条件下研究区径流控制率Table 2 Runoff control rate of study area under different rainfall return periods

根据模拟结果数据利用回归分析的方法对降水量和径流控制率关系分别进行线性、二次、三次以及指数函数曲线拟合，得到径流控制率与降水量的函数关系如式(7)～(10)所示，其中式(7)为线性函数拟合(图7)，其确定系数R2为0.944；式(8)(9)分别为二次、三次函数拟合，其R2分别为0.996和0.998；式(10)为指数函数拟合，R2为0.988。

RAV=-0.007q+0.925

(7)

RAV=0.000 061 49q2-0.014q+1.019

(8)

RAV=0.000 000 383 6q3+0.000 005 222q2-0.012q+1.008

(9)

RAV=0.998 062 889 657 683 8e-0.013 626 295 055 132 58q

(10)

式中q为降雨强度。

由图7可见，本研究降雨强度与径流控制率模拟结果使用三次函数决定系数更高，更加符合结果所表征的关系。所有的拟合函数均揭示了径流控制率与雨强呈负相关关系，与实际情况相符。

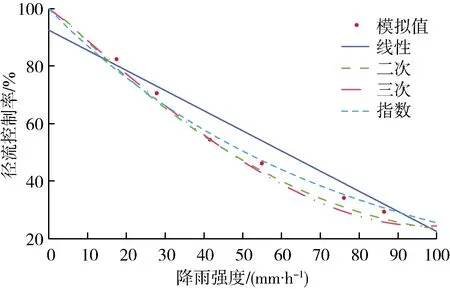
图7 降雨强度与径流控制率拟合函数Fig.7 Fitting function of rainfall intensity and runoff control rate

通过对天福和园小区径流控制率随降雨重现期变化的模拟，发现在重现期增大时，降水量增大，海绵措施及绿地通过下渗控制的水量减少，更多的径流通过排水管网排出，故随着重现期的增大，径流控制率从1年一遇的82.5%逐渐减小到100年一遇的29.4%；在较小重现期，即降雨重现期小于10 a时，重现期增大时，降雨强度变化较大，径流控制率随重现期的变化较大。当降雨重现期大于10 a时，相较于较小重现期条件，降雨强度远超管网设计标准，LID措施下渗逐渐饱和，对径流控制效果有所减弱，径流控制率随降雨重现期的增大变化趋于平缓，从1年一遇到10年一遇，径流控制率减小36.4%，从10年一遇到100年一遇，径流控制率减小16.7%。

4 结 论

a. 所应用的耦合管网系统的二维城市雨洪过程模型适用于海绵城市径流控制率的模拟评估，模拟精度较高，对于海绵城市建设模拟评估有借鉴意义。

b. 天福和园小区径流控制率的模拟表明，随着降雨重现期的增大，径流控制率逐渐减小，当降雨重现期为1 a时，径流控制率为82.5%，降雨重现期为100 a时，径流控制率为29.4%。

c. 在降雨重现期较小时，降雨重现期的变化对径流控制率影响较大，如当降雨重现期从1 a变化为10 a时，径流控制率减小36.4%。当降雨重现期较大时，径流控制率随降雨重现期的增大逐渐趋于平缓，如重现期从10 a增长到100 a时，径流控制率只降低16.7%。

d. 根据模拟结果，采用回归分析的方法得到不同降雨重现期降雨强度与径流控制率的拟合关系，拟合函数表明降雨强度与径流控制率呈负相关关系。