我国股指期货市场波动跳跃行为研究
2020-11-19李佳
李 佳
(武汉大学 湖北 武汉 430000)
一、引言
在资产价格研究中,早期学者认为收益率是一个高斯过程,但Manderbrot(1963)研究发现资产价格的收益率具有尖峰厚尾特征,从而否定了资产价格收益率遵循高斯过程的假设。随后有研究表明,资产价格在短时间内可能产生大幅度波动,即发生跳跃行为。跳跃一旦发生,会对股指期货市场产生巨大冲击,所以对我国股指期货市场跳跃行为研究具有非常重要的意义。
对资产价格跳跃现象进行研究,检测与估计跳跃行为是前提。对波动跳跃行为检测与估计方法通常有两种:一种是以模型估计为基础的参数方法,另一种是以高频数据为基础的非参数方法。
参数方法基于随机过程,Press(1967)假定对数资产价格是布朗运动和具有泊松分布的随机过程的线性组合,后者代表跳跃行为;Chan等(2002)设置跳跃幅度为类似自回归的ARMA过程,提出自回归跳跃幅度模型;Maheu等(2004)把过去跳跃加入GARCH波动率方程,从而丰富了GARJI模型,研究表明过去跳跃不能影响波动率的非对称性,不对称性是由当前跳跃引起的。非参数方法利用高频数据,先估计出已实现波动率和连续性波动,然后用二者估计量之差来估计跳跃波动成分。Andersen等(1998)定义已实现波动率是日内收益率的平方之和,并用已实现波动率作为真实波动率的估计,因此只要估计出积分波动率,就可以使用二者之差来估计波动率中的跳跃成分。在这个领域具有里程碑意义的成果是Barndorff-Nielsen和Shephard(2006)构造的BN-S检验统计量,检验的思路是用已实现波动率与二次幂变差之差估计波动率中的跳跃成分,判断是否发生跳跃行为。随后很多学者对BN-S检验进行改进,提出了相应的跳跃检验统计量。如Huang等(2005)延续了BN-S检验的思路提出了Z检验统计量,但其缺陷是在存在市场微观结构噪音的情况下,由于相近的高频收益率具有一定程度的相关性,从而将价格的连续性波动错误推断为跳跃波动;所以Corsi等(2010)对Z检验统计量进行改进,使用交错的高频收益率作为已实现二次幂变差以及已实现三次幂变差的估计基础,从而得到跳跃波动部分。
参数方法利用的是离散的低频数据,不能包含资产交易过程中的全部有用信息,而非参数方法可以充分使用高频数据中包括的有用信息来估计跳跃波动成分,因此简单的非参数方法估计的结果也会比复杂的参数模型更有效。
针对我国金融市场跳跃特征,国内学者进行了大量实证分析。如陈国进等(2010)基于沪深300指数高频数据,对波动率中连续波动部分和跳跃成分两种波动进行估计并分析其特征,指出我国股指具有显著的跳跃聚集特性且两种波动的滞后相关性比美国市场更久;杨科等(2012)指出我国股市波动率和跳跃波动表现出聚集性,而且跳跃发生的频率比较高;王明涛等(2017)指出沪深300股指期货的跳跃次数日效应明显,滞后3阶的跳跃幅度对它起正向作用,当天和前天的跳跃幅度和跳跃次数大幅增加和降低波动的连续部分。
上述研究为我国证券市场资产价格跳跃行为提供了较为具体的检测方法、分析思路和对策建议,对资产价格波动率的预测、跳跃风险管理等具有积极意义。本文使用修正的Z检验统计量检测和估计跳跃波动,在估计波动率的过程中考虑到市场微观结构噪声的影响,使用核估计量对已实现波动率进行纠偏,然后对三个股指期货市场的跳跃波动进行研究和对比,分析我国股指期货市场的跳跃行为特征。
二、跳跃行为检测的理论基础
已有研究指出即使是很容易的非参数方法模型效果也比复杂的参数方法要好。因此本文拟采用C-TZ检验估计噪声纠偏后的已实现波动率中的跳跃波动成分。
(一)BNS检验
假定股票的对数价格pt遵循跳跃扩散过程:
dpt=μtdt+σtdWt+dJt
(1)
其中,μt是漂移项,σt是严格为正的随机波动过程,Wt是标准布朗运动,Jt是t时刻的泊松跳跃过程。
对数价格从0到t时刻的二次变差为:
(2)

(3)
Barndorff-Nielsen和Shephard(2004)指出,当每日观测得到的价格个数趋于无穷大时,连续性波动可以用二次幂变差BVt来估计。即:
(4)
这样波动率中的跳跃成分可以表示为:
(5)
设定原假设为资产价格没有发生跳跃,检验统计量Ht大于临界点时,就可以拒绝原假设认为第t个交易日内发生了跳跃。表示如下:
(6)
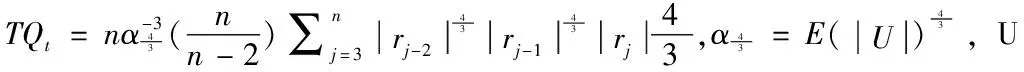
(二)Z检验
继承了BNS检验方法的基本思路,Huang等人提出了Z检验统计量。其统计量如下:
(7)
其中,TPt为三次幂变差。在交易日没有发生跳跃行为的条件下,当nt→∞时,Z检验统计量渐进服从标准正态分布。
当Z统计量大于标准正态分布在显著性水平α上的临界值φα时,可以推断跳跃是显著存在的。
(三)C-TZ检验
但是Corsi等(2010)指出在连续跳跃发生的频率很高的情况下,有一部分跳跃Z检验统计量检测不出来。因此他们提出修正的Z检验统计量,即C-TZ检验统计量。
已实现门阀多次幂变差定义为:
(8)
其中,Ι(.)是示性函数,φt是严格为正的一个随机门阀函数。在一定条件下,已实现门阀多次幂变差能够依概率收敛,即:
(9)
(10)
其中Zγ(x,y)的表达式为:
(11)
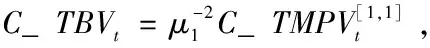
(12)
在没有跳跃行为时,当nt→∞时,C-TZ统计量渐进服从标准正态分布。当C-TZ检验统计量大于在显著水平α上标准正态分布的临界值φα时,可以认为存在显著的跳跃行为。基于C-TZ统计量,第t日的跳跃波动为:
(13)
三、波动率估计模型的构建
(一)波动率估计的噪声纠偏
本文用已实现波动率RV作为波动率的估计,RV的计算基于有效价格,即市场不存在任何摩擦时的有效价格。事实上市场摩擦无处不在,因此当前市场价格与资产内在价值有一定偏差,这两者之间的差异称为市场微观结构噪声。当使用高频数据时,微观结构噪声的影响非常明显,因此本文采用已实现核估计来对波动率进行纠偏。
已实现波动率RV的定义是日内高频收益率平方之和,即:
(14)
Hansen和Lunde(2006)提出的已实现核估计量对波动率进行如下纠偏:
(15)
(二)跳跃行为的估计
对已实现波动率进行噪声纠偏后,利用纠偏后的已实现波动率序列,估计波动率中的跳跃成分。采用C-TZ检验统计量,第t天波动率的跳跃成分为:
(16)
第t天的绝对跳跃为:
(17)
四、我国股指期货市场跳跃行为实证分析
(一)数据选择及说明
本文数据基于沪深300股指期货、中证500股指期货和上证50股指期货三个研究对象的5分钟高频数据,最终选取2016年1月8日至2018年4月30日沪深300股指5分钟交易数据共27950个、中证500股指期货5分钟交易数据共27950个、上证50股指期货5分钟交易数据共27950个。数据来源于万德,实证部分利用Matlab完成。
(二)连续性和跳跃性波动的描述性统计分析
表1是对三个研究对象的已实现波动率进行噪声纠偏后得到的已实现波动率的描述性统计指标。由表可知中证500股指期货的波动率标准差最大,为2.5032e-04,沪深300股指期货次之,上证50股指期货最小。这说明中证500股指期货的投资风险较大,上证50股指期货投资风险较小。这与三个股指期货标的指数样本股的选取有很大联系。
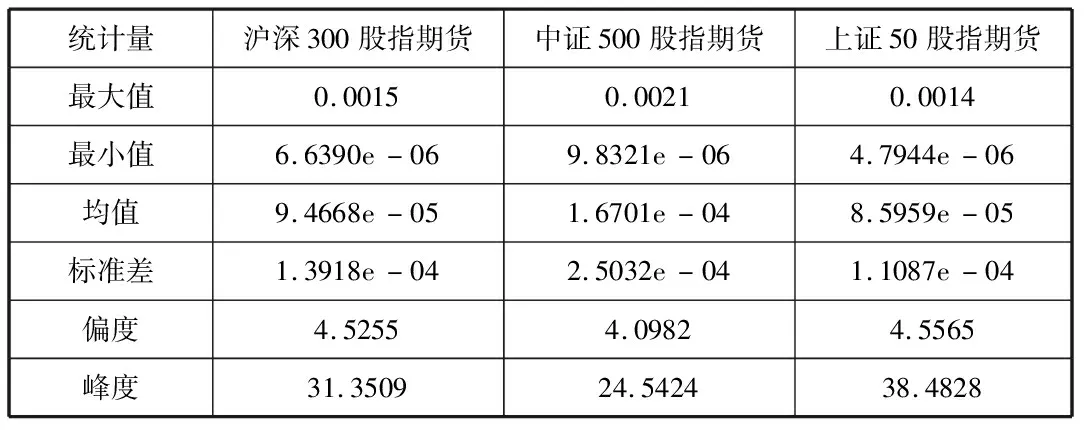
表1 噪声纠偏后波动率序列统计特征
图1为95%置信水平下,三个研究对象波动率跳跃序列图。图中可以看出,虽然三个市场跳跃幅度和跳跃频率相差较大,但在某些时刻三个市场会同时受到新信息冲击发生共同跳跃。无论是考虑跳跃频率还是跳跃幅度,中证500股指期货都比其他两个市场大很多,发生大幅度跳跃的可能性也高很多,上证50股指期货跳跃幅度最小。这是因为中证500指数的样本股选取的是中小市值公司,而上证50指数样本股选取的是龙头企业,无论从流动性还是公司估值模型看,小盘股更容易出现大涨大跌现象。
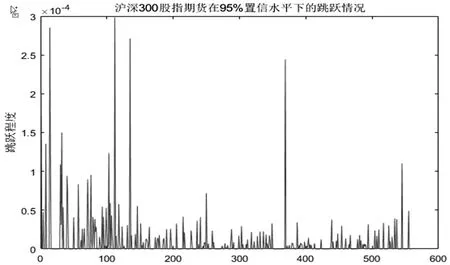
图1 95%置信水平下的正跳跃序列
表2为三个研究对象的相关系数。由表可以发现三个研究对象的跳跃序列相关系数较高,这说明三个股指期货市场受新信息冲击同时发生跳跃的频率较高。
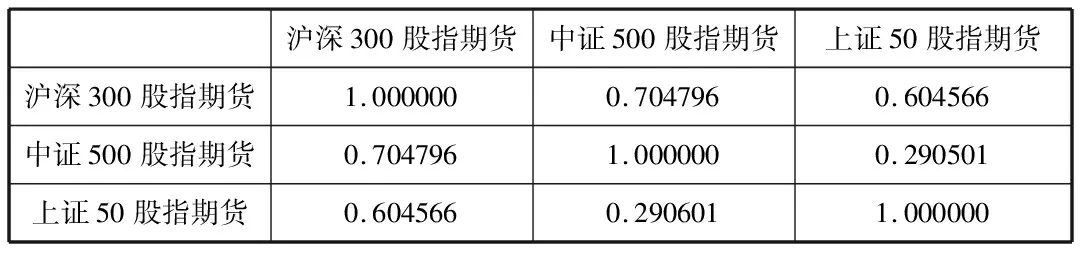
表2 三个研究对象的相关系数
(三)跳跃行为的特征分析
表3是95%置信水平下三个研究对象正跳跃序列的特征。表中可以看出,中证500股指期货的跳跃幅度最强,所有跳跃中最大值为7.7703e-04,均值为1.8131e-05,远大于其他两个股指期货市场,说明中证500股指期货容易受到信息冲击,从而发生大幅度的跳跃行为。考察标准差方面,中证500股指期货的标准差也远大于其他两个研究对象,说明其跳跃波动最大。而上证50股指期货不仅跳跃幅度小,且其标准差几乎是中证500股指期货的三分之一,跳跃波动平稳。沪深300股指期货介于两者之间。三个研究对象都呈现右偏、尖峰现象。
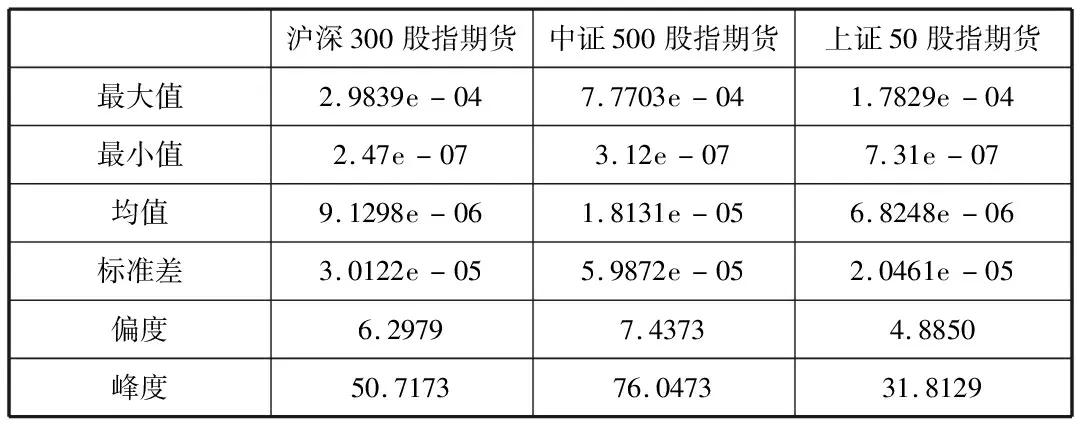
表3 三个研究对象的跳跃序列特征
表4是95%置信水平下三个研究对象绝对跳跃序列的特征,可以发现结论与上述基本一致。
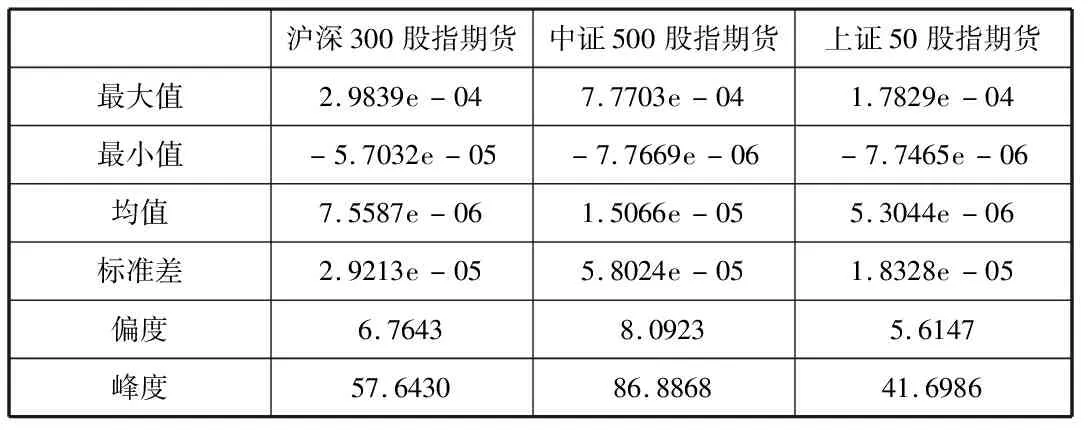
表4 三个研究对象的绝对跳跃序列特征
表5为三个研究对象跳跃方差对总方差的贡献序列的特征。表中可以看出,三个研究对象跳跃行为发生时跳跃方差占总方差的比例大部分在50%以下,均值在27%到29%之间,说明跳跃波动与连续性波动相比较小,连续性波动构成已实现波动率的大部分。其中上证50股指期货跳跃方差对总方差的贡献最大。
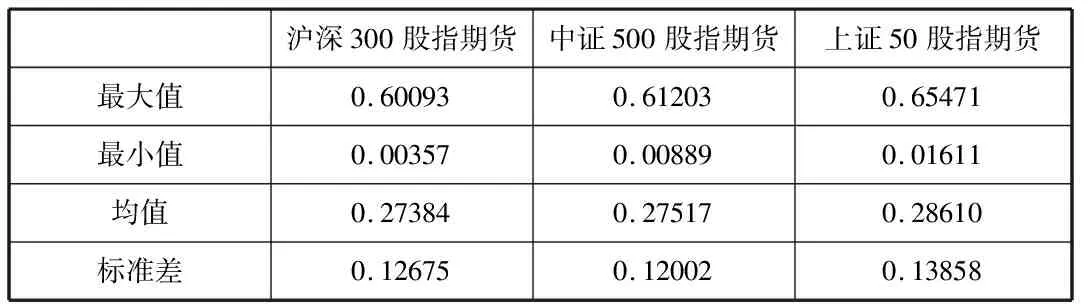
表5 三个研究对象跳跃方差对总方差的贡献序列的特征
五、总结及建议
本文以非参数方法为理论依据,基于沪深300股指期货、中证500股指期货、上证50股指期货的五分钟高频数据,估计出噪声纠偏后的已实现波动率中的跳跃波动成分,进而分析跳跃波动的影响因素和特征,主要结论有:
(1)我国股指期货市场总体上发生跳跃的可能性较大,三个研究对象中中证500股指期货发生跳跃的可能性最大,沪深300股指期货的跳跃频率次之,上证50股指期货发生跳跃的可能性最低。在跳跃的聚集性方面,三个市场发生连续跳跃的可能性非常小。
(2)中证500股指期货的跳跃强度最大,远大于另外两个股指期货,沪深300股指期货的跳跃强度次之,中证500股指期货的跳跃幅度最小。
(3)三个股指期货跳跃波动的相关系数较高,发生共跳的可能性较大。
由于我国股指期货市场投机氛围较为严重,投资者更多地关注资本利得,在市场上容易追涨杀跌,放大了市场风险,导致我国股指期货市场价格发生跳跃的频率整体较高。所以,投资者应理性投资,不能盲目追涨杀跌。
