防滑铲对公路斜坡软弱土路堤稳定性的影响

2020-11-18黄立葵刘致浩唐恩宽

公路工程 2020年5期

黄立葵, 刘致浩, 唐恩宽

(1. 湖南大学土木工程学院，湖南长沙 410082；2. 中国建筑第五工程局有限公司，湖南长沙 410004)

0 引言

我国西南山区的公路和铁路建设经常遇到斜坡软弱土路基。与水平软弱土路基相比，斜坡软弱土路基更容易出现边坡失稳现象[1-2]。阿尔及利亚南北高速公路希法段位于该国北部，路线穿梭于崇山峻岭之中，地形起伏较大，有多处斜坡路堤，且斜坡路堤大部分位于泥灰岩或泥岩等软弱土层上。为提高斜坡软弱土路堤的稳定性，设计中采用了在路堤坡脚处设置防滑铲的防护方案。防滑铲断面为倒梯形，采用透水性天然碎砾石料填筑，不仅置换了软弱土，还能起到排水的作用，防止路堤坡脚的抗剪强度因地下水的作用而降低[3]。与国内外增强斜坡路基稳定性的一般方法比较，防滑铲的结构新颖，操作简单，具有良好的可操作性和经济性，能为道路边坡防护带来很大的经济和社会效益。

现有涉及此种处治措施的研究文献较少，且多是定性描述。吴玉[4]等采用极限平衡法对防滑铲应用于斜坡软弱土路堤的工作机理进行了讨论，其考虑的路堤模型根据铁路路基设计规范建立，且将进行条分的土体假设为刚体，未考虑土体的弹塑性本构关系以及变形对应力的影响。为此，本文运用有限元分析软件ABAQUS，建立设置防滑铲的公路斜坡软弱土路堤模型，采用强度折减有限单元法，对比分析有无防滑铲这2种情况下路堤模型的稳定安全系数，得到稳定安全系数K与斜坡软弱层厚度的关系，并提出相应的组合优化措施，以期对国内的防滑铲应用提供借鉴。

1 计算模型

土体本构模型采用目前工程分析中最普遍的理想弹塑性模型，屈服准则为摩尔-库伦准则，并假定按平面应变问题考虑，建立如图1所示的防滑铲应用于斜坡软弱土路堤计算模型。参考《公路工程技术标准》(JTG B01-2014)，取路堤宽度30 m，路堤中心线高度8 m，路堤边坡坡度为1∶1.5，斜坡软弱层厚10 m，斜坡坡度为1∶5。于路堤坡脚处设置两侧坡度为1∶1，底宽6 m的倒梯形防滑铲，路堤坡脚落于防滑铲顶中间位置，防滑铲的埋置深度为4 m。材料参数参考工程经验及相关公路设计规范，见表1。

图1 设置防滑铲的公路斜坡软弱土路堤模型Figure 1 Embankment model with anti-slide shovel on weak soil slope

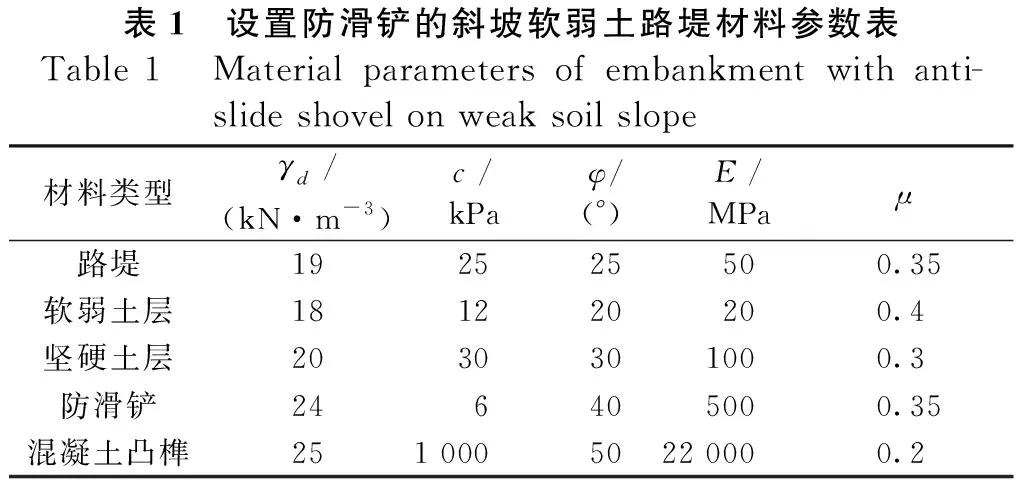
表1 设置防滑铲的斜坡软弱土路堤材料参数表Table 1 Material parameters of embankment with anti-slide shovel on weak soil slope材料类型γd/(kN·m-3)c/kPaφ/(°)E/MPaμ路堤192525500.35软弱土层181220200.4坚硬土层2030301000.3防滑铲246405000.35混凝土凸榫251 0005022 0000.2

2 分析方法

匀质边坡的稳定性分析方法，目前主要包括极限平衡法和数值分析方法。强度折减有限单元法是在诸多分析法中，应用广泛、前景良好的一种数值分析方法。此方法将强度折减理论与有限元计算技术相结合，可直接得到边坡的圆弧滑动面和稳定安全系数[5]。

此方法的基本原理是，将路堤材料的实际抗剪强度指标c、φ值同时进行折减，折减方式如式(1)所示。

(1)

式中:c′、φ′值为折减后新的抗剪强度指标，然后将c′、φ′值作为新的输入参数进行试算。如果此时有限元计算收敛，稍微增大折减系数Ftrial后得到另一组抗剪强度指标，再次进行试算，直到有限元计算发散。则有限元计算最后一次收敛所对应的折减系数Ftrial即可定义为斜坡软弱土路堤的稳定安全系数K，即:

(2)

(3)

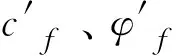
3 结果分析与讨论

3.1 有无防滑铲时圆弧滑动面比较

路堤边坡的滑动面一般呈现曲面，通常称之为圆弧滑动面。塑性应变的发展体现了路堤土体剪切破坏的发展过程，是破坏土体内所产生不可恢复的变形分量，故塑性应变的发展能够描述边坡土体的滑动面变化。

图2分别是有无防滑铲时模型在自重荷载作用下的等效塑性应变云图。没有设置防滑铲时见图2(a)，等效塑性区从路堤坡脚处通过，塑性区范围较大，应变值也较大；设置防滑铲时见图2(b)，等效塑性区下移，基本位于防滑铲底部，塑性区较小，没有形成贯通，且应变值较小。

(a) 未设防滑铲

3.2 参数折减后圆弧滑动面变化

按照前述参数折减的方法，修改摩尔-库伦弹塑性模型参数值，可得参数折减后的等效塑性应变云图，分别如图3、图4所示。未设防滑铲时，取折减系数Ftrial=1.10，路堤坡脚处的等效塑性区增大，但有限元计算是收敛的，说明在此折减系数情况下边坡是稳定的；加大折减系数，取Ftrial=1.20，从等效塑性应变发展趋势可知，等效塑性应变向上延伸，且有无限发展的趋势，坡脚有明显的突变，表明此时边坡已达到临界极限状态；继续加大折减系数，取Ftrial=1.22，有限元计算不收敛，故此种情况下斜坡软弱路堤的稳定安全系数即为1.20。

(a) Ftrial =1.10

设置防滑铲时，取折减系数Ftrial=1.15，防滑铲底部的等效塑性区向防滑铲右部外延，整体有向右上角翘起的趋势，但在此折减系数下边坡仍是稳定的；加大折减系数，取Ftrial=1.27，云图显示，等效塑性区已经贯通到软弱层顶面，防滑铲整体的转动已经较大，说明此时边坡已处于临界极限状态；继续加大折减系数，取Ftrial=1.28，有限元计算不收敛，故此种情况下斜坡软弱路堤的稳定安全系数即为1.27。图3和图4表明，斜坡软弱路堤的稳定安全系数由无防滑铲时的1.20增加到有防滑铲时的1.27。

(a) Ftrial =1.15

3.3 不同软弱层厚度条件下防滑铲对稳定性的影响

软弱层厚度显著影响路堤的横向变形[6]。假设图1模型基本不变，改变斜坡软弱层的厚度，按照前述强度折减有限单元法，图5给出了在软弱层厚度分别为2、4、6、8、10 m的条件下，有无防滑铲的斜坡软弱土路堤稳定安全系数K的变化情况。

由图5可以看出，在同等条件下，设置防滑铲能提高稳定安全系数，但是软弱层厚度的不同会影响稳定安全系数提高的程度。在未设置防滑铲的情况下，软弱层厚度为2 m时，稳定安全系数K为1.27；当软弱层厚度大于或等于4 m时，K值基本保持在1.20。设置防滑铲后，当软弱层厚度不大时，即防滑铲的底部嵌固在下卧刚硬层中，稳定安全系数提高到了1.42，比未设防滑铲时增大11.8%；当软弱层厚度为4 m时，即防滑铲的底部刚好接触于下卧刚硬层，K值提高到了1.40，比未设防滑铲时增大15.7%；稳定安全系数在软弱层厚度为4～6 m的过程中有较大降低，由1.40降到了1.27，且在大于6 m后基本保持在1.27，此时的K值比未设防滑铲时只增大5.8%。

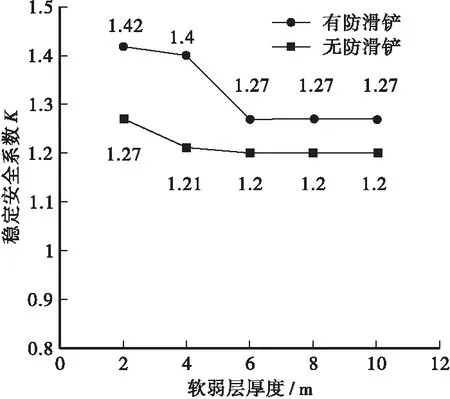
图5 稳定安全系数与斜坡软弱层厚度的关系Figure 5 Relationship between coefficient of stability safety and soft layer thickness

3.4 优化设计

以上讨论表明，当软弱层厚度不大时，防滑铲对斜坡软弱路堤的稳定性明显提高。当软弱层厚度过大时，单纯设置防滑铲对提高稳定性的效果不大，此时可与其他措施组合起来使用，比如在防滑铲底部正中间的位置设置一个上宽下窄的混凝土凸榫[7]，如图6(a)所示。假设凸榫材料采用C15混凝土，上宽2.5 m，两侧坡度为1∶6，底部刚好深入到下卧硬土层上，材料参数见表1。由图6(b)可见，在8m斜坡软弱土层内增设混凝土凸榫后，由于凸榫刚度大，防滑铲在荷载作用下将要发生转动的趋势被抑制，斜坡软弱土层基本不产生应变，应变主要发生在凸榫左上方的防滑铲内。继续应用强度折减有限元法，计算得到此时的稳定安全系数为1.35，比仅设置防滑铲又提高6.3%。不难预见，适当加强防滑铲的整体性可使安全系数进一步增大。