考虑土拱效应的双向增强复合地基沉降计算

张 玲, 邓 云, 欧 强, 黄 璇

(1.湖南大学 岩土工程研究所，湖南 长沙 410082；2.福州理工学院，福建 福州 350506)

0 引言

联合水平向土工加筋垫层与竖向桩体复合地基组成的双向增强复合地基技术虽已推广应用于公路、铁路及建筑工程等领域，但其设计计算理论，特别是沉降计算仍亟待进一步深入研究。

针对桩承式路堤的双向增强复合地基的沉降计算方法而言，已有不少学者在各自不同的假定条件下，提出了各自的沉降计算方法。例如：张玲[1]等将加筋垫层视为弹性地基梁、桩和桩间土视为一系列不同刚度的弹簧，根据Euler-Bernoulli梁理论推导出双向增强地基的沉降计算表达式。赵明华[2]等基于弹性理论的解答，考虑以加筋体在单桩范围内的部分为研究对象，推导了空间情况下水平加筋体变形函数。DED[3]结合Pasternak剪切模型和薄膜模型去分析加筋垫层，建立了土工格栅加筋垫层+碎石桩双向增强复合地基的承载变形分析模型。但上述方法都是将路堤荷载视为由路堤填料自重引起的均布荷载，未考虑由于桩土刚度差异导致的路堤填料内部应力重分布的影响，这将导致路堤荷载的不均匀分布。

然而，已有的双向增强复合地基数值模拟和试验研究成果表明[4]：由于桩土刚度差异较大而引起的桩土差异沉降，以致由双向增强复合地基支撑的路堤填料中有可能有土拱效应的影响，并且土拱效应对地基的承载变形性状影响还比较大。为此，不少学者在薄膜模型的基础上，采用不同的路堤土拱分析模型，对双向增强复合地基中的水平加筋垫层的受力变形进行分析[5-6]。

桩承式加筋路堤土拱效应研究，目前主要有TERZAGHI提出的平面土拱效应，LOW等提出的半圆形模型、俄国学者普罗托奇雅阔诺夫的自然平衡拱理论以及H&R提出的半球形土拱模型等，上述模型通常是将土拱轴线假设为平滑的悬链线或半圆弧等，而土拱形成条件则是假定固定土拱底部或着土拱拱顶处于极限平衡状态，这都是是基于土拱形成条件及土拱形状提出的极限平衡模型。此外，国内、外学者从沉降相等的面出发，在太沙基理论的基础上，深入研究了桩承式路堤土拱效应分析的“土柱模型”，从而获得了桩承式路堤桩土荷载分担比与桩土差异沉降之间的关系，然而该模型脱离了土拱形状，未考虑布桩形式对桩土应力比的影响。

此外，薄膜模型主要反映了土工加筋体的拉膜效应，薄膜的变形多为“抛物线假设”或“圆弧假设”，计算简便。但薄膜模型也存在一定的不足，未考虑加筋垫层的抗弯特性，仅适用于单层土工织物的加筋垫层。而对于多层土工材料加筋垫层或土工格室等三维加筋材料形成的加筋垫层，其抗弯刚度不容忽视，在荷载调节方面，主要表现为柔性筏板效应[7-8]。

本文采用自然平衡拱理论进行土拱效应分析，再考虑加筋垫层的柔性筏板效应，基于弹性地基梁理论，提出考虑土拱效应的双向增强复合地基沉降计算公式。

1 计算模型的建立与分析

1.1 土拱模型分析

如图1所示，选取路堤中心线上两桩中心距范围内的土柱为研究对象，路堤高H，重度为γ。复合地基中桩的直径或边长为dp，桩中心距为s，分析时将圆形截面桩等效为方形截面桩，等效方桩的边长d=0.9dp，桩间净距为s′=s-d。双向增强复合地基是非常复杂的三维空间问题，若将其简化为二维平面问题，本文则按参考水平受荷桩桩体计算宽度的取值方法来确定计算宽度[2]，即：

(1)

式中：dp为桩的直径或边长；kf为桩形状换算系数，方形截面桩的kf=1.0，圆形截面桩的kf=0.9。

(a) 剖面图

路堤填土中的土拱效应是在填土荷载作用下产生不均匀沉降而引起填土不均匀位移，路堤填土调整自身变形以承载自重而形成的。自然形成的路堤土拱，其形状及结构必然是最合理的，因为土体具有抗压强度较高、抗拉强度低的特点，所以拱轴线上剪力、弯矩为零，只有轴力。根据结构力学分析，如图2所示，则拱轴线方程为：

图2 路堤土拱受力分析Figure 2 Force analysis of soil arch on emban km ent

(2)

式中：f为拱高，也可视为形成完整土拱所需的最小路堤填土高度。

根据力的平衡条件，可以求出桩顶荷载pp为：

(3)

桩间土所分担的荷载ps，即土拱下部土体荷载，ps=bγy

(4)

1.2 加筋垫层变形分析

本文采用Timoshenko地基梁理论(计入剪切变形)来讨论加筋垫层受力变形。视加筋垫层为一长s、宽b、抗弯刚度D和剪切刚度C的地基梁，忽略其水平位移，仅考虑其在路堤荷载作用下的竖向挠曲变形，垫层与桩土加固区计算模型如图3所示。桩和桩间土视为不同刚度的弹簧，桩间土可提供的竖向反力qs为：

qs=bksws

(5)

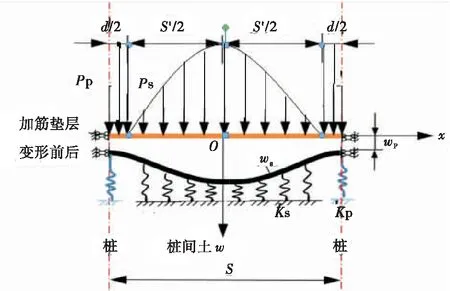
图3 土工加筋垫层受力变形分析Figure 3 Force and deformation analysis of geosynthetic reinforced cushion layer

式中：ks为桩间土地基反力系数，与土的性质和基础尺寸有关，可通过室内模型或现场载荷试验确定也可查经验值表粗估；ws为桩间土的沉降。

桩用线性弹簧来模拟，桩的弹簧刚度kp为：

(6)

式中：Kp为桩的刚度系数，kN/m，其值可取Q～s曲线上的切线或割线斜率。对灌注桩，当无实测资料时也可按经验公式Kp=10Pa计算[9]，其中Pa为单桩容许承载力，kN。

若假定桩横截面上各点的沉降相同，则可仅用一根弹簧来模拟桩，并假定某一变形量下桩弹簧上作用的荷载pp为：

pp=bkpwp

(7)

式中：wp为桩顶沉降。

基于图3所示坐标系，根据荷载及地基反力的情况，将右半部分(0≤x≤s/2)分成两段，其长度从左到右分别为：l1=s′/2和l2=d/2。则在分段上部荷载ps、pp作用下, 作用于Winkler弹性地基上Timoshenko梁的平衡微分方程可表示为：

(8)

式中：D和C分别为加筋垫层的抗弯刚度和剪切刚度，其中剪切刚度C=kAGe，其中k为截面剪切系数，由形状确定，通常矩形截面k=5/6；A是梁的截面积；土工合成材料一般只承受拉力，不受剪切力，故剪切模量为颗粒层的剪切模量为Ge=E/2(1+v)，其中E是弹性模量，v是泊松比。

由方程(8)推导出Timoshenko梁的控制微分方程：

(9)

式(9)中：

因此四阶常系数非齐次方程(9)的通解为：

(10)

式(10)中：

将式(10)代入方程(8)，并求导可得转角φ：

(11)

则加筋垫层的弯矩M=-Dφ′，即：

(12)

则加筋垫层的转角φ可改写成：

φ=eax

(13)

则加筋垫层的剪力Q=C(w′-φ)，即：

以各地类面积为因变量(Y)，以社会经济指标为自变量(X)，进行相关分析，计算土地利用变化与社会经济驱动因子之间的相关系数[13]，构建各地类面积与社会经济指标的多元逐步回归模型(表7)[17]。

(14)

式中: 待定系数c1，c2，c3，c4通过以下边界条件确定：

(15)

将式(14)分别代入式(11)、式(12)，可以求出c1，c2，c3，c4与f有关，再根据受力平衡条件求出f：

(16)

式中：A=bs；Ap=bd；As=bs′。

根据式(12)计算确定出0≤x≤s/2各点的沉降后，可得桩土差异沉降Δs：

ΔsΔ=ws|x=0-wp|x=0.5s′

(17)

由上述分析可见，地基梁的挠曲变形与路堤荷载ps、pp有关，而路堤荷载的重分布又是由路堤填土土拱效应引起的，而土拱效应的发挥程度又取决于桩土的差异沉降。因此土拱效应、加筋垫层变形和复合地基沉降是一个非常复杂的耦合系统，难以直接求解。此外，其中Δs在另一方面也反映了加筋垫层刚度及路基填土的一系列物理性质。

2 算例分析

遂宁—重庆铁路某一试验路段的地势较为平整，且表面覆盖层为呈软塑状的冲洪积软土，厚度6～12 m，冲洪积软土下层为呈中硬塑状的粉质黏土，土体的物理力学参数如表1所示。表中:γs为土层的平均重度；w为含水量；e为孔隙比:φ为内摩擦角；c为粘聚力；Es为压缩模量。在实际施工时，采用红层软岩作为填料进行路基填筑，填筑高度大约为11.0 m，边坡坡率1∶1.5，路堤顶部宽12.0 m。经过专家评审，决定采用粉喷桩对地基进行加固处理，设计桩径为0.5 m，桩间距采用1.0 m，其中桩长需满足完全穿过软土地基并嵌入到基岩中至少0.5 m的条件，并且要求粉喷桩顶部的厚度达到0.5 m，铺设的两层双向土工格栅碎石垫层两层抗拉强度为50 kN/m。土工格栅碎石垫层自上而下分别为0.1 m厚碎石层、土工格栅、0.3 m厚碎石层、土工格栅以及0.1 m厚碎石层。更为详细的工程背景资料可详见文献[10]。

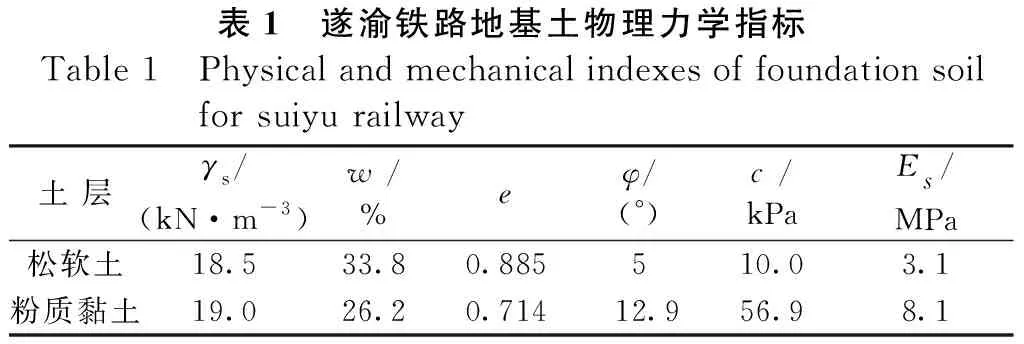
表1 遂渝铁路地基土物理力学指标Table 1 Physical and mechanical indexes of foundation soil for suiyu railway土 层γs/(kN·m-3)w /%eφ/(°)c /kPaEs/MPa松软土18.5 33.80.885510.0 3.1 粉质黏土19.0 26.20.71412.956.98.1

采用本文方法对遂渝铁路ZY1与ZY2断面的地基沉降进行预测，计算所需参数如下：路堤填土重度γ=19 kN/m3，弹性模量Ee=20 MPa，泊松比νe=0.3；土体弹簧刚度系数由ks=1.2Es/[b×(1-μs2)]估算，土的压缩模量Es取值见表1，泊松比νs取0.3，故ZY1和ZY2断面的ks1=5750 kN/m3，ks2=4 250 kN/m3，土体的屈服位移sus取35 mm；桩的弹簧刚度系数kp由式(6)估算，其中桩刚度Kp由经验公式Kp=10Pa计算，故ZY1和ZY2断面的Kp1=1 800 kN/m，Kp2=2 000 kN/m，取加筋垫层的弹性模量为80 MPa。

按本文方法计算所得不同填筑高度时ZY1和ZY2断面路堤中心线沉降值及其与沉降观测结果的比较见表2。由表2可见，与实测值相比，本文方法计算得到的路堤中心沉降值误差在允许范围内，验证了本文方法的合理性。

表2 路堤中心线沉降计算值与观测值的比较Table 2 Comparison of the calculated settlements and the measured ones in the mid-span of the emban km ent填筑高度/mZY1断面ZY2断面实测值/mm文献[2]计算/mm本文方法/mm实测值/mm实测值/mm本文方法/mm717.518.218.122.326.522.5922.322.524.329.432.128.91027.224.227.231.736.532.11128.634.528.535.740.235.3

3 参数分析

由上述考虑土拱效应的双向增强复合地基沉降计算模型可知，土拱效应的发挥与路堤填土高度、桩净距、桩土刚度比等因素相关，而且还与桩土差异沉降相关。现对以上参数进行简要分析。

图4、图5分别表示土拱高度与填土高度、桩净距的关系曲线。分析可知：土拱高度与路堤填土高度成正比，随着桩净距的增大先增大，后来趋于稳定。

图4 拱高与路堤高度关系Figure 4 Relationship between f and h

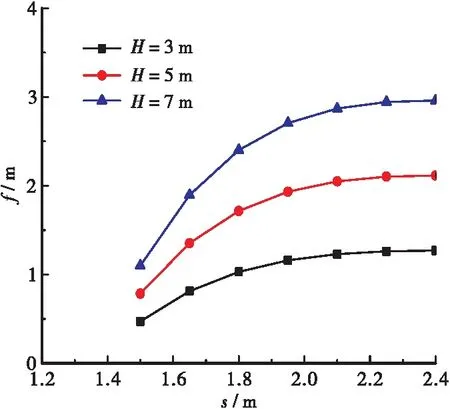
图5 土拱高度与桩净距的关系Figure 5 Relationship between f and s

图6、图7分别表示桩土差异沉降与桩土刚度比与土拱高度的关系曲线。由图6可知桩土差异沉降随着桩土刚度比的增大而减小；由图7分析可知土拱高度随着桩土差异沉降的增大而增大。

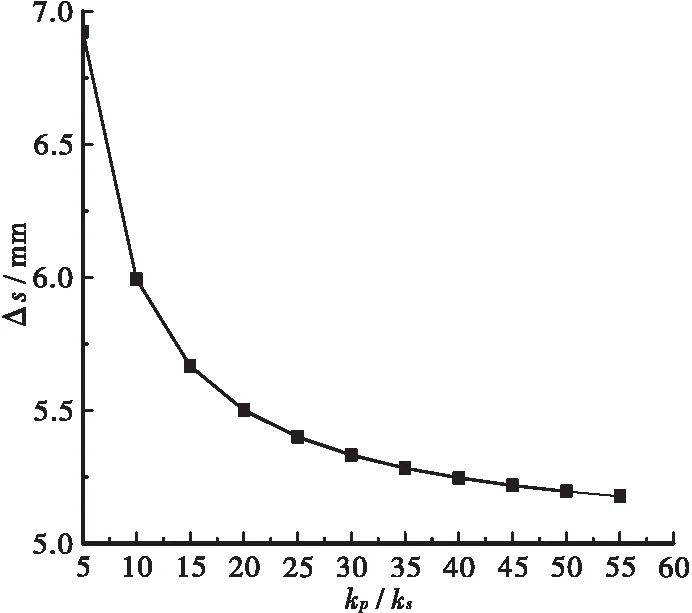
图6 桩土差异沉降与桩土刚度比的关系Figure 6 Relationship between Δs and kp/ ks

图7 拱高与路堤高度关系Figure 7 Relationship between f and Δs

4 结语

本文借助自然平衡拱理论分析路堤填料土拱效应，视土工材料加筋垫层为弹性地基上的Timosh-enko梁，桩与桩间土视为不同刚度的弹簧，基于弹性地基Timoshenko梁理论，推导出双向增强复合地基沉降计算公式。结合工程实例验证了本文方法的可行性。本文方法具有如下特点：

a.本文的双向增强复合地基沉降计算方法可考虑路堤填土—加筋垫层—复合地基三者之间的相互作用。

b.结合工程实例：探讨了土拱效应的发挥不仅与路堤高度、桩体复合地基桩间距布置等因素密切相关，而且与桩土差异沉降的发展密切相关。

c.以地基梁模型分析加筋垫层，可考虑加筋垫层抗弯拉性能对路堤下双向增强复合地基承载变形特性的有利影响，更适合于多层土工格栅等二维土工材料或土工格室等三维土工材料加筋垫层构成的双向增强复合地基的沉降分析。

但本文方法忽略了加筋垫层水平位移、地基土变形的非线性特性等因素的影响，进一步的研究仍待继续。