基于S型曲线的五次多项式轨迹规划

杨友良 孟文龙

(华北理工大学电气工程学院 河北 唐山 063210)

为了满足机械臂末端及关节的运动参数对应于时间的变化关系，保证机械臂完成期望的空间运动提高农业生产力，解决劳动力不足，降低工人劳动强度，提高工人劳动舒适性，降低作业成本，提出了一种基于S型曲线的五次多项式轨迹规划。在直线插补的基础上，带有圆弧过渡的折线插补优化算法，在一定程度上对路径进行了优化，并提高了机械臂运动的稳定性。对正弦速度曲线、梯形速度曲线和S型速度曲线进行分析，并基于三种速度曲线进行五次多项式轨迹规划，得出一种效果较好的规划方法。

引言

随着科学技术的发展进步，农业也在朝着机械化、信息化、数字化的方向发展。国内外许多学者对摘果机器人进行了研究，包括摘果机器人本身、避障、摘果、识别与定位等[1-3]。采摘机器人在自然环境中工作，比在工业环境中更加复杂。目前，机器人主要基于计算机视觉技术对采摘环境进行重构。轨迹规划是对机械臂末端及关节的运动参数对应于时间的变化关系，保证机械臂完成期望的空间运动。为了使机械臂工作可靠且稳定，所以要求所用的轨迹关于时间的曲线是平滑且连续的，保证曲线波动不大[4-5]。机械臂的运动轨迹指的是：机械臂末端在自由空间内运动时，所有的位姿总和。而机械臂轨迹规划则是使机械臂到达目标位姿要求时，对速度和加速度等运动参数的设计。轨迹规划的目的是保证机械臂快速、准确且稳定完成路径规划的任务。轨迹规划与路径规划的区别是：路径规划只是对末端路径进行空间搜索，与时间无关；而轨迹规划则是对机械臂末端及关节的运动参数对应于时间的变化关系，保证机械臂完成期望的空间运动。为了使机械臂工作可靠且稳定，所以要求所用的轨迹关于时间的曲线是平滑且连续的，保证曲线波动不大。

一、轨迹规划

(一)笛卡尔坐标系下轨迹规划

笛卡尔坐标系(也称为直角坐标系)下的轨迹规划指的是末端执行器依据任务要求到达目标位置(相对于基坐标系的位置)。当任务要求末端执行器沿着直线或者是曲线运动时，将位姿描述时的直角坐标用时间函数表示。但考虑到机械臂的实际情况，电机都会安装在关节处，所以需要将规划目标有末端转换到关节位置，即将末端执行器的坐标变量通过运动学反解，转换到关节变量中去，如图1。

图1 规划流程

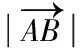
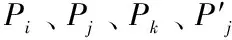
(二)关节空间下轨迹规划

在进行轨迹规划的过程中，将关节参数以时间函数表示。在笛卡尔坐标系下进行轨迹规划时需要对大量的插补点进行运动学反解，运算量巨大，效率低。且在您笛卡尔坐标系下的轨迹规划会出现奇异问题，造成速度失控等问题。在进行关节空间轨迹规划时，必须要注意的是要保证运动的平稳性和连续性，进而提高机械臂的使用寿命和效率，如图2。

图2 关节空间轨迹规划流程图

二、S型曲线轨迹规划

考虑本文所用的路径搜索算法生成的路径在自由空间内有许多中间节点，采用笛卡尔坐标系的轨迹规划，虽然能满足通过中间点，但运动反解产生大量的计算，影响工作效率。所以，提出了一种分步式的关节空间轨迹规划算法，即先选用合适的速度曲线对中间节点进行速度的规划，再利用所得中间点的速度，进行关节空间的轨迹规划。两种轨迹规划算法在位移和速度的曲线是平滑且稳定的，但五次多项式轨迹规划加速度的曲线是平滑的，保障的机械臂运动的速度不会发生突变，提高电机的使用寿命。选用的轨迹规划算法以五次多项式为基础，进行分步规划。首先，分别以正弦速度曲线、梯形速度曲线和S型速度曲线对路径中间节点进行速度规划，得到中间节点的速度；然后利用五次多项式的计算方法进行轨迹规划仿真验证，从而得出最佳的组合方式,(1)基于梯形曲线的五次多项式轨迹规划梯形曲线表达式的计算：已知总的运动时间为T，对加速度a、加速时间t1、匀速时间t2和减速时间的计算：

(1)

t2=T-t1-t3

(2)

(3)

(4)

(2)基于正弦曲线的五次多项式轨迹规划正弦曲线表达式的计算：已知总的运动时间为T，则：

(5)

(6)

(7)

仿真结果如图3所示。

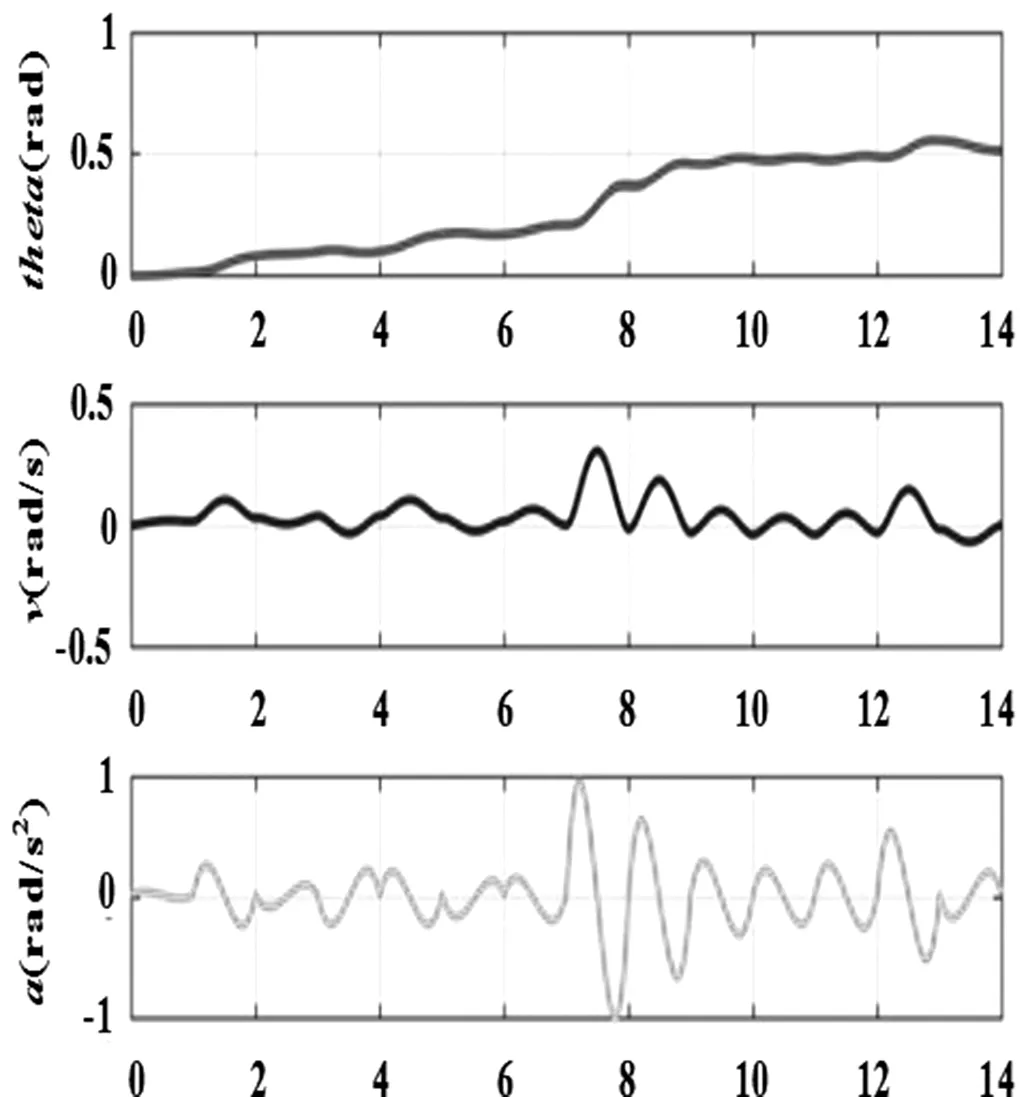
图3 基于正弦曲线的五次多项式轨迹规划

(3)基于S型曲线的五次多项式轨迹规划S型曲线表达式的计算：已知总的运动时间为T，取七段曲线的时间相同为t，仿真结果如图4所示。

图4 基于S型曲线的五次多项式轨迹规划

三种轨迹规划的结果在角位移方面差别不大，但基于S型速度曲线在速度和加速度的稳定性较好，波动较小，而且角加速度相对较小，有利于机械臂的平稳运行。

三、结论

轨迹规划是保证机械臂能够平稳运行的基础。对笛卡尔坐标系下轨迹规划的两种方法进行分析。首先，在笛卡尔坐标系下轨迹规划方面，分别对直线插补和圆弧插补进行介绍。考虑到上一章搜索结果为折线，在直线插补的基础上，提出一种带有圆弧过渡的折线插补优化算法，在一定程度上对路径进行了优化，并提高了机械臂运动的稳定性。但在笛卡尔坐标系下进行规划需要进行大量的反解运算，数据处理量大。然后，对关节坐标系下的两种方法进行了分析，并基于速度稳定性的考虑，采用了五次多项式的方法。对正弦速度曲线、梯形速度曲线和S型速度曲线进行分析，并基于三种速度曲线进行五次多项式轨迹规划，得出一种效果较好的规划方法——基于S型曲线的五次多项式轨迹规划。