基于不确定度分析的计算结果有效数字确定方法

张馨睿，吴飒，陈仁军，周学亮

（1.北京航空航天大学，北京 100083； 2.陆军装备部航空军事代表局，上海 200233；3.苏州天航长鹰科技发展有限公司，苏州 215155）

背景

在科学研究与工程实践中，不可避免地要进行大量的数据计算，也就是把一些数值作为已知量，通过规定的计算方法以数值的方式给出运算结果。无论是作为已知量还是作为运算结果的数值都是通过有效数字的方式给出，也就是说这些数值在本质上具有一定的不确定性。数据计算不仅应当按照计算方法给出理论结果，也应当把来自于数据源和计算方法的不确定度信息正确地传递给计算结果的使用者，一般是以有效数字位的方式完成数据结果和不确定度信息的传递。因此，如何确定计算结果的有效位数是十分必要的，不正确的有效数字位会造成计算结果中所传递的不确定度被错误地使用。正是因为有效数字位与不确定度存在着本质上的关联，因而有必要通过不确定度分析的方法进行有效数字位的确定。

1 概念

1.1 有效数字的含义

数据的来源一般有两种途径，一种是通过直接测量得到的测量量，另一种是通过计算的得到的计算结果。对于第一种情况，有效数字是反映被测量大小的全部数字，包含准确数字以及一位带有不确定度的估读数字。有效数字的最末一位是估读的，因此只有最末一位数字具有不确定度，有效数字的不确定度代表了估读数字的不确定度，可以通过有效数字的不确定度大小来确定哪位数字是估读数字。有效数字也在一定程度上表达了测量结果的不确定度[2]，其最末数字位数离小数点越近，被测值的不确定度越大。对于第二种情况，通过对计算结果的修约得到其有效数字。无论是直接测量值还是通过间接计算得到的数值，当以有效数字表示时，都要遵循只有最末位是估计值，其他位都是准确数字的要求。只有这样才能保证正确反映出分析量的多少，才能使结果被正确使用。

1.2 不确定度的含义

不确定度的概念首先应用在测量结果的表述中，用以合理表示被测值分散程度。无论是直接测量量还是通过计算得到的测量值，其结果的完整表示应该是被测量量加上相应的不确定度。不确定度反映了测量的质量，不确定度小，表明测量结果距真值的偏离范围就越小，质量就越高，其使用价值就越高，相反，不确定度越大，则偏离范围就越大，质量就越低，其使用价值就越低。

2 测量不确定度评定

进行测量不确定度评定时，比较常用的方法是应用测量不确定度传播率的方法（GUM法），具体过程包括建模、标准不确定度评定、计算合成标准不确定度和计算扩展不确定度。

2.1 建模

被测量的值的不确定度取决于参与计算的其他分量，确定这种取决关系即为建模。被测量Y的最佳值y由X1，X2，…，XN的最佳值x1，x2，…，xn得到，即y=f(x1，x2，…，xn)。y的标准不确定度 u(y)取决于 x1，x2，…，xn的标准不确定度。

2.2 标准不确定度评定

A类评定方法是为了得到测量数据的标准差的最佳估计值，通过一系列测量数据使用统计方法进行评定。通常使用方法有贝塞尔法、最大残差法、极差法、最小二乘法。

B类评定方法是通过非统计方法进行的，B类评定方法中最常见的是使用来自于技术资料、证书或手册中提供的数据。这些数据往往提供了可能的取值范围，但其概率分布要进行假设，根据已知信息可假设为正态分布、均匀分布、反正弦分布、双均匀分布、三角分布，如果信息缺乏，一般情况下可以假设为均匀分布。

2.3 合成不确定度计算

合成不确定度是在不确定度传播公式下，自变量的标准不确定度经函数关系传播到因变量所产生的不确定度。不确定度传播公式为：

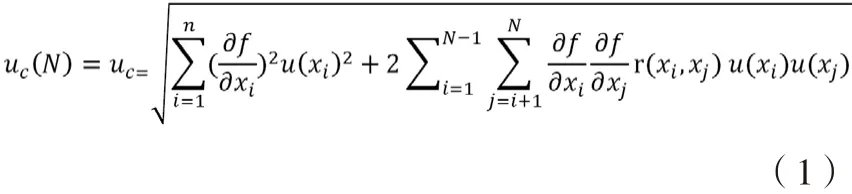
假设自变量之间互不相关，则r(xi，xj) =0合成不确定度公式为：

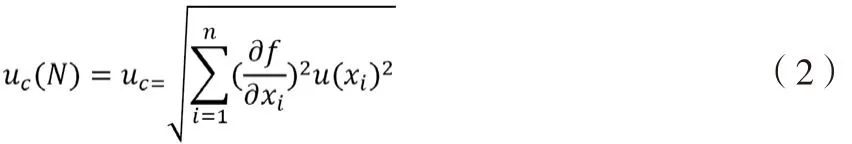
2.4 扩展不确定度计算

扩展不确定度表示测量值大部分合理地包含在此区间内，扩展不确定度由合成不确定度与包含因子相乘求得：

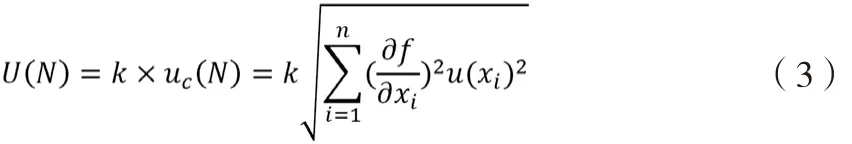
包含因子常用求取方法如下[3]：

1）当参与运算分量的自由度已知时，根据下式（4）计算合成不确定度的有效自由度

vi—u(xi)的自由度。

由t分布求出包含因子P为置信水平，可取0.95，0.99，0.997，可根据t分布表，通过p与v查表得tp(v)，即k。

2）当参与运算分量的自由度未知时，可通过赋值法求取k。

实际测量工作中，大多数测量量的分布可以近似为正态分布，对于正态分布的情况，包含因子取决于期望的置信概率。在工程上一般的置信概率取值为90 %、95 %、99 %，对应的包含因子分别为2、2.56、3。其他分布情况，也有类似的幅值方法，具体可以参阅测量不确定度评定和数理统计相关书籍。

3 计算结果的不确定度

计算结果的不确定度评定与测量的不确定度评定非常类似。

3.1 建模

计算结果的来源公式即为模型。

3.2 标准不确定度评定

计算所面临的情况不存在一系列测量数据，不使用统计方法进行评定，因此不使用A类评定方法。

计算过程的不确定度应使用B类评定方法进行评定，数据可来源于资料或前期计算结果，因此在进行标准不确定度评估时，参与计算的每个数值都是不确定度评定时的来源。如果数值给出了不确定度信息，则可以利用该信息计算其标准不确定度。如果该数值仅以有效数字给出，由于没有给出其他信息，故假设其为均匀分布，根据修约规则，其量值变化半宽度为a，标准不确定度等于

3.3 合成标准不确定度计算

计算结果的合成标准不确定度计算与测量不确定度计算类似。

合成标准不确定度是在不确定度传播公式下，参与计算分量的标准不确定度经灵敏度系数传播到计算结果所产生的不确定度。不确定度传播公式为：

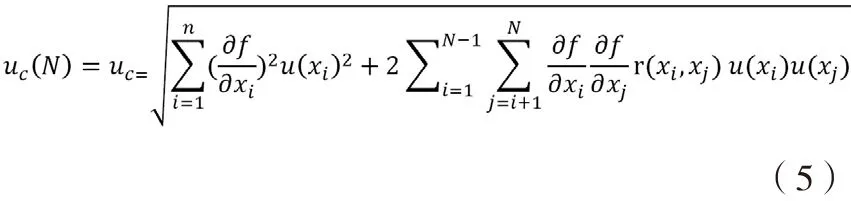
假设参与计算的分量之间互不相关，则r(xi，xj) =0，合成标准不确定度公式为：

3.4 扩展不确定度计算

计算结果的合成标准不确定度计算与测量不确定度计算类似，扩展不确定度由合成不确定度与包含因子相乘求得：

k通过赋值法求得，取决于预期的置信概率，在工程上一般的置信概率取值为90 %、95 %、99 %，对应的包含因子分别为2、2.56、3。

4 计算结果的有效数字确定

4.1 常规方法

数值计算是科研工作的核心，计算公式可以是常规的算术计算，也可以是非常复杂的计算方法。下面就几种常见的计算方法，给出目前采用的有效数字确定原则[1]。

加减法：最终结果的有效数字的末位与参与运算变量中有效数字末位最高位者相同。

乘除法：最终结果的有效数字的位数与参与运算变量中有效数字位数最少者相同。

乘方运算：最终结果的有效数字位数与底数有效位数相同。

对数运算：最终结果的有效数字位数与真数的有效位数相同。

4.2 基于不确定度分析的方法

有效数字的不确定度与最末一位修约数字有直接联系，无论是直接测量还是间接计算得到的结果，其不确定度都表现了计算结果在哪个数位上是不确定的，确定有效数字位数即确定修约数字在哪位，可以通过计算结果的大小与其不确定度来确定。进行最终结果报告时，结果的末位应与不确定度的末位保持一致（如GJB 3756）。在进行计算时，根据修约规则，有效数字中只包含一位不确定数字就是最末一位修约数字，因而对于不确定度的关注只有一位数字即首位数字。根据预期的置信概率对应的包含因子，得到扩展不确定度，然后根据通用的修约规则，得到只有一个数字位的数值，如该位数值大于等于5，则有效数字位进一位，否则有效数字位保持不变。例如0.04对应的有效数字位是小数点后第二位，0.05对应的有效数字位是小数点后1位[5]。

4.3 在常用计算方法中的应用

1）加法：N=f(x1，x2，…xn)=x1±x2±…±xn

合成不确定度：

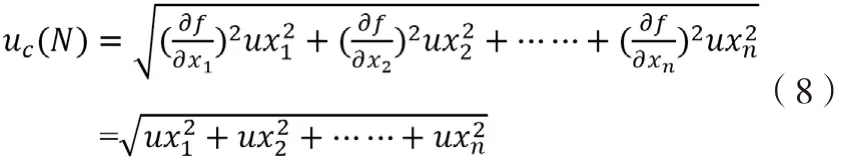
这是最简单的计算过程，当只有一个数值具有最少有效数字时，它将占主导地位，其他数值的影响可以忽略。通过公式就可以明显看出。这种情况下与常规方法是一致的。

只有当存在多个数值具有相同的最小有效数字时，才需要根据不确定度传播公式计算其合成标准不确定度。

2）乘法：N= f(x1，x2，…xn)=x1×x2×…×xn

合成不确定度：

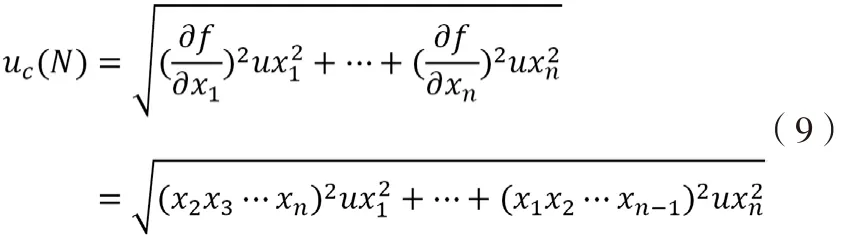
3）除法：N= f(x1，x2，…xn)=x1÷x2÷…÷xn

合成不确定度：

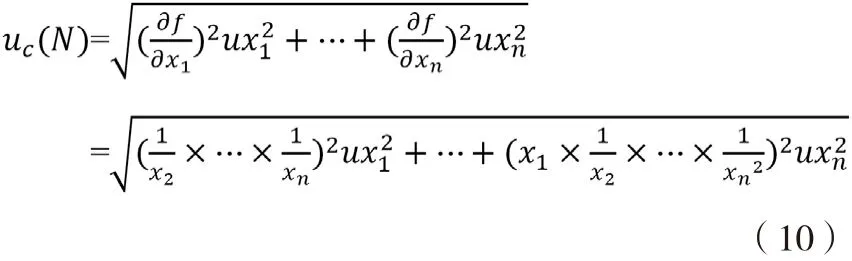
4）乘方（以平方运算为例）：N=f(x)=x2

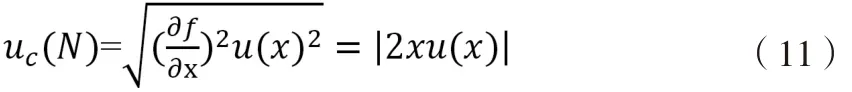
合成不确定度：

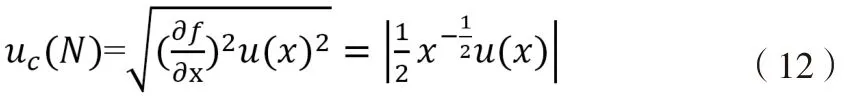
6）对数:N=f(x)=logax

合成不确定度：

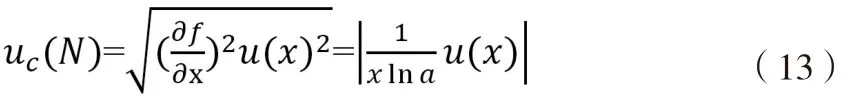
7）指数:N=f(x)=ax

合成不确定度：

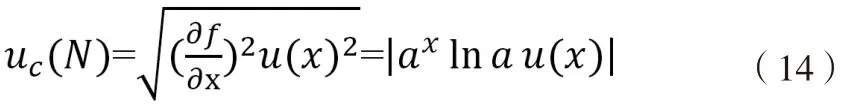
5 示例与分析

5.1 加减法运算

在加减法运算中，如若参与运算的分量中最小有效数值只有一个时，其产生的不确定度占主导地位，其他数值产生的不确定度可以忽略，因此这种情况下，常用的确定方法与本文提出的确定方法得出的结果相同。

例 1：N=x1+x2+x3+x4+x5+x6，x1=1.325，x2=1.364，x3=1.102，x4=1.32，x5=1.364，x6=1.182，计算结果N=7.657。

1）使用本文提出的确定方法：

x1、x2、x3、x4、x5、x6服从均匀分布，其标准不确定度为

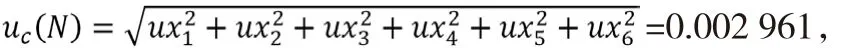
由于只有一个数据占主导，且假设其为均匀分布，因而认为计算结果也基本服从均匀分布，其扩展不确定度为，0.002 961×2≈0.006故有效位进一位即0.01，按照修约规则N的最终表示结果是N=7.66。

2）使用常用确定方法：

参与运算的有效数字中小数位数最少者为2，因此最终计算结果中保留的小数数位也是2位，最终计算结果为7.66。两种方法给出了同样的结果，原因是在加减法运算中，灵敏度系数是常数1，只有一个数据具有最小的有效位，在本文提出的方法中不确定度取决于最小有效位；常规方法中也取决于最小有效位。

例 2：N=x1+x2+x3+…+x100，x1=x2=x100=0.013 25，N=1.325

1）使用本文提出的方法：

x1、x2、…、x100服从均匀分布，其标准不确定度为

由于每个数据的不确定度都相同，且假设其为均匀分布，因而认为计算结果也基本服从均匀分布，其扩展不确定度为0.002 89×2≈0.005，故有效位即0.01，按照修约规则N的最终表示结果是N=1.33。

2）使用常用确定方法：

参与运算的最小有效数位为4，因此运算结果的有效数位也是4位，最终计算结果为1.325。

当参与加减法运算的变量修约数字所在位数相同且变量个数增加到一定程度时，采用两种方法得到的结果是不同的，原因是由于变量个数的增加使得扩展不确定度扩大了十倍，有效位也随之发生改变，此时常用的方法仍根据变量中小数位最小者确定有效位是不合理的。

5.2 乘法运算

V=a×b×h，a=5.375，b=4.230，h=4.110， 结 果 为V=93.445 987 5。修约截尾产生的不确定度属于均匀分布，标准不确定度

按正态分布95 %置信概率的包含因子为2，则扩展不确定度为0.02，确定有效位是与不确定度首位，最终表示结果是V=93.45。而采用常规方法，最终表示结果的有效位是所有数据中最小有效位数，表示结果是V=93.446。

采用两种方法得到的结果是不同的，原因在于采用常规方法时将不确定度传播中的灵敏度系数全部看作常数1，采用本文提出的方法，在进行不确定度传播计算时，真实的考虑了灵敏度系数，参与运算变量的灵敏度系数大于常数1，因此得到的结果会偏大。

5.3 除法运算

5.4 平方运算

E=v2，v=6.23，计算结果 E=38.812 9。则。按正态分布95 %置信概率的包含因子为2，则扩展不确定度为0.035 972×2≈0.1，确定有效位是与不确定度首位，最终表示结果是v=38.8。而采用常规方法，最终表示结果的有效位是底数有效位数，表示结果是v=38.8。

5.5 开方运算

5.6 对数运算

y=log10x，x=20.11计算结果y=1.303 412，标准不确定度，则0.000 062 3，按正态分布95 %置信概率的包含因子为2，则扩展不确定度为0.000 062 3×2≈0.000 1，确定有效位是与不确定度首位，最终表示结果是y=1.303 4。而采用常规方法，最终表示结果的有效位数与真数的有效位数相同，表示结果是y=1.303。

6 结论

本文基于不确定度传播原理对确定计算结果有效数字的方法，计算由自变量修约截尾产生的标准不确定度传播到测量值的合成不确定度，计算结果有效数字的确定与扩展不确定度相关，计算结果的有效位与扩展不确定度的首位相同。采用常用方法与本文提出的方法得出的结果是有差异的，原因在于常规的方法由于没有考虑计算中各数据对不确定度的贡献是与计算方法中该变量的偏导数有关的，因而会造成一定的偏差，本文提出的方法考虑了在不确定度传播过程中灵敏度系数的影响，根据不确定度更准确地确定了有效位，文中举例说明两种确定法则的差异。使用本文提出的方法进行有效位的确定仍然会造成不确定度的失真，因此在最终计算结果的表示形式上以有效位加不确定度共同表示较为合理。