基于CST仿真的双脊喇叭天线设计
2020-11-18姚泽南刘浩明叶瑀
姚泽南,刘浩明,叶瑀
(广东省医疗器械质量监督检验所,广州 510663)
1 喇叭天线介绍
喇叭天线的是一种面天线,由于其工作频带宽,增益高,结构简单而且具有较高的功率容量,喇叭天线有非常广泛的应用。喇叭天线常被用来作为测试用标准天线[1],因而在医疗器械电磁兼容测试中有较高的应用价值。
喇叭天线由两部分组成:第一部分为波导管,它的主要起能量传输作用;第二部分为喇叭,喇叭部分可以看做是由波导在横截面逐渐展开形成的[2]。波导管将输入的信号传送给喇叭,信号在逐渐张开的喇叭部分被激励,谐振辐射出去。
矩形波导是波导管的一种,矩形波导中能够传输的电磁波模式一般称为TEmn(Transverse Electric)模式,即横电模式,指的是电场方向与传播方向垂直。其中m表示波导x方向的宽度与半波长的比值,n表示波导y方向的宽度与半波长的比值。如图1所示矩形波导的各种工作模式,z轴为电磁波传播方向。
矩形波导管内部的主模是TE10模,也叫横电波模式。这种模式的传播方向是沿着z轴方向的,其电场分量垂直于电磁波的传播方向,并且平行于矩形波导的y轴方向,电场分量的大小沿着宽边x轴变化。所以矩形波导的宽边长度a等于半波长λ/2。如果a等于半波长的整数倍(倍数大于1),则把这种电磁波称为该矩形波导的高次模。高次模对应更高的频率,所以在传输时衰减的更快。
2 角锥喇叭天线理论分析
本文设计的双脊喇叭天线是基于角锥喇叭天线演变而来的,分析角锥喇叭天线有助于理解双脊喇叭天线的工作机制,对角锥喇叭的分析,通常是将H面喇叭和E面喇叭进行向量叠加。
1)根据天线理论,辐射口径面越大,辐射就越强,辐射的方向性也越好。如果没有喇叭部分,只是在矩形波导末端面开口,那么在开口处也能产生电磁辐射,但因为辐射的口径面太小,所以由矩形波导直接开口产生的辐射场很弱。如果在波导末端连接一个渐变的喇叭形状的开口,那辐射口径面积就增大了,辐射增强,方向性也增强。
2)如果没有喇叭部分,在矩形波导末端面开口,那么在开口处电磁波呈现的波阻抗就有很大不同,电磁波就会大量反射,而未得到有效的辐射。传输效率必然较低。如果波导口连接渐变的喇叭口径,那么电磁波在经过此处就有一个渐变的过程,与空间就能形成更好的阻抗匹配,从而更好的将能量传输到空间,提高了电磁波的传输效率。
图2为喇叭天线的口径面示意图,以H面喇叭天线为例,假定H面喇叭的矩形波导的TE10模式电波被激励。H面喇叭天线是矩形波导沿着宽边x逐渐扩展形成的,因此其口面场Es=Esy的相位沿着宽边x逐渐变化,由于窄边y保持不变,所以Esy相位沿窄边y方向上的分布与矩形波导相同,矩形波导的末端x逐渐扩张。
图2中Rx、Ry分别为H面和E面喇叭天线的长度;Dx、Dy分别为H面喇叭天线的口径长度;O为天线的相位中心,它相当于喇叭天线的等效辐射中心,也就是说电磁波是由这个等效源点发射出来的。可以推导出相移量最大值为:

也就是说,H面扇形喇叭天线的相位却沿x方向而变化,口面场Esy方向沿y轴方向。假设口面中心O为相位零点,在口面上x方向边沿处,口面场Esy的相移量最大,相位随坐标变量呈平方率分布。
同理,对E面扇形喇叭天线,口面沿着窄边y逐渐张开,口面场Esy相位沿y轴方向发生变化,而相位沿x轴保持不变,在y轴边沿处,相移量取最大值。

对角锥喇叭天线,由于宽边x、窄边y同时张开,在这两个方向上口面场相位也会相应变化,与此对应的相位最大值为:

也就是说,最大相移量沿宽边和窄边均按平方率变化。
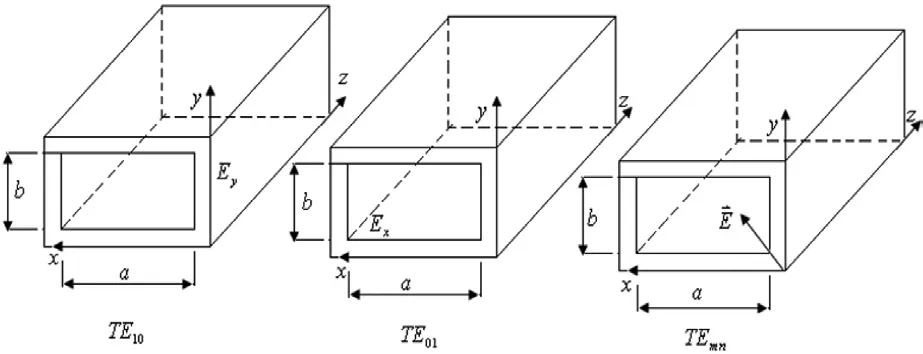
图1 矩形波导的几种工作模式
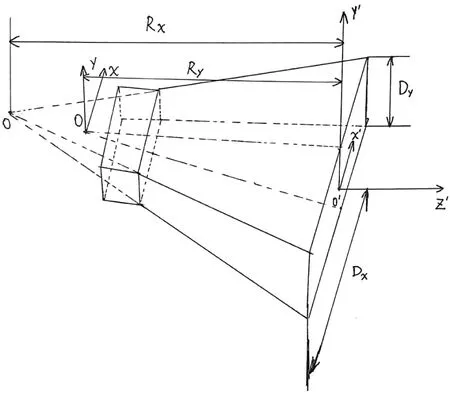
图2 喇叭天线的口径面示意图
角锥喇叭天线的口面场振幅和相位分布可以用以下公式来表达:

从以上公式可以看出,不管角锥喇叭天线口面是沿着哪个边逐渐展开,其口面场的振幅沿窄边方向是均匀的,而沿宽边方向按余弦规律变化,口面场的相位随变化的那条边呈现平方率变化。
3 双脊波导设计参数分析
双脊波导可以展宽喇叭天线的工作频带,双脊喇叭天线可以看成是由逐渐张开的脊波导构成,对于它的分析可以从分析脊波导入手。
相对于矩形波导,脊波导有许多优点。因为脊波导中脊凸起,其等效电长度就增长了,所以在相同的工作频率下,脊波导天线的尺寸就可以做的更小。同时,因为TE10模式电波的截止波长就比矩形波导更长,单模传输的频率范围就展宽了[3]。
为了分析加脊波导展宽带宽的原因,本文采用等效电路法来分析。根据双脊波导与单脊波导中的场分布,图3给出了其等效电路[3],从图中可以看出,电容由两部分构成:脊波导凸起的平面部分引入的电容Cp,脊波导两边角引起的边缘电容Cf。
因为磁场主要分布在脊的两侧,单位长度电感值为L0,令脊波导中填充的介质的介电常数ε,可以得到Cp=εa2/ b2,边缘电容:
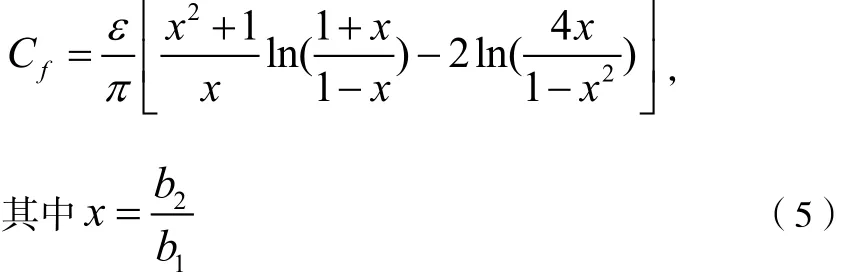
式中,脊波导的总电容C=Cp+2*Cf。单位长度的总电感,其中 μ 为波导中填充介质的磁导率。脊波导中各个参数可以按照如下公式计算[4]:
脊波导的截止频率fc
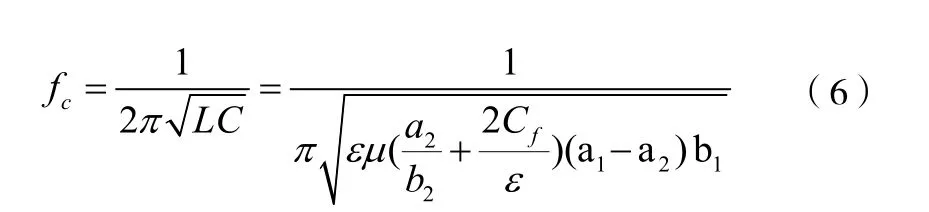
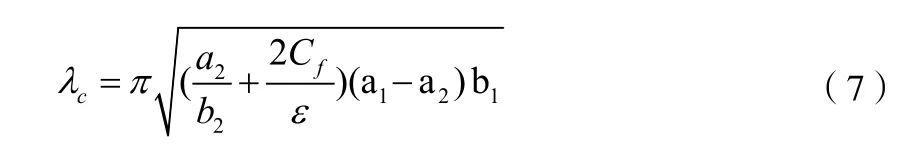
公式(6)、(7)是根据单脊波导来计算的,根据以上公式可以很简单的求出双脊波导的截止频率和截止波长,双脊波导的等效电容是单脊波导的1/2,等效电感是单脊波导的2倍,所以双脊波导和单脊波导的截止频率与截止波长是相等的[5]。
4 双脊喇叭天线设计与仿真试验
双脊喇叭天线波导部分和喇叭辐射段部分组成,其中在波导部分有同轴-波导转换段、后腔两个部分。同轴线穿过一个脊的中心,与另外一个脊相连,起到馈电的作用[5]。后腔可以减小后向辐射对前向辐射的影响。喇叭辐射段由喇叭和渐变的双脊组成,这两个脊一般呈指数渐变,喇叭部分的这种渐变设计可以改善波导与空间的匹配,形成更好的辐射性能。
对于双脊喇叭天线,脊波导段部分的长度应小于最高工作频率的半波长[6],同轴线一般选择50 Ω的特征阻抗,同轴线外导体与脊波导中的一个脊接触,内导体延伸到脊波导的另外一个脊上并与之形成良好的接触。从同轴线进入的电磁能量通过两个脊波导之间的内导体进入到波导部分,通过调节双脊后腔的尺寸,可以实现同轴和波导部分的良好匹配。电磁能量经过喇叭部分辐射出去。
要设计出工作频率为1~8 GHz喇叭天线的具体尺寸,首先需要确定波导截面的尺寸。
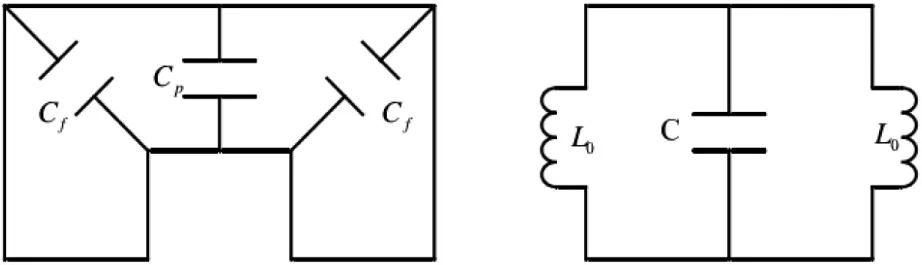
图3 截止状态下脊波导等效电路
根据分析,喇叭段长度应大于最低频率波长的二分之一,避免激励高次模,最低频率为1 GHz,根据波长计算公式:

得出最低频率的半波长为150 mm,为了尽量小型化,喇叭长度L取150 mm。喇叭口面大小根据天线增益来计算,为了尽量小型化同时保证天线的增益,喇叭口面处取宽边w取为200 mm,窄边h取为140 mm。
喇叭天线加脊后,天线带宽会明显增大,确定脊的形状,一般选择指数双脊,即脊结构形状曲线为指数形式[7],脊间距是根据阻抗匹配来调节的,不妨设置其初始值s为2 mm,双脊喇叭天线的脊曲线方程为

该曲线经过(0,s/2)和(L,h/2),这样可以求解出A和k关于C的函数:

在CST(Computer Simulation Technology)中将C设置成变量,就可以扫面不同指数对天线的影响。公式(7)给出了波导尺寸的指导,本文设置初始长度a=90 mm,b=63 mm,C=0.01,图4为建立的初始模型。
在CST中进行仿真,初始参数仿真的驻波比如图5所示,从图中可以看出,仿真的结果基本满足喇叭天线的预计,但驻波比在5.18 GHz时出现了一个峰值,而一般天线的要求是VSWR<2,所以还需要对天线进行优化,下面对其关键参数进行分析扫描,以调整得到最优参数。
脊曲线的形状、双脊间距对天线匹配的影响最大,下面分别对这些因素进行扫描优化以得到最优匹配。
分析波导部分的宽边长度a对VSWR的影响曲线,从结果中可以看出,a的变化对驻波比影响较小。
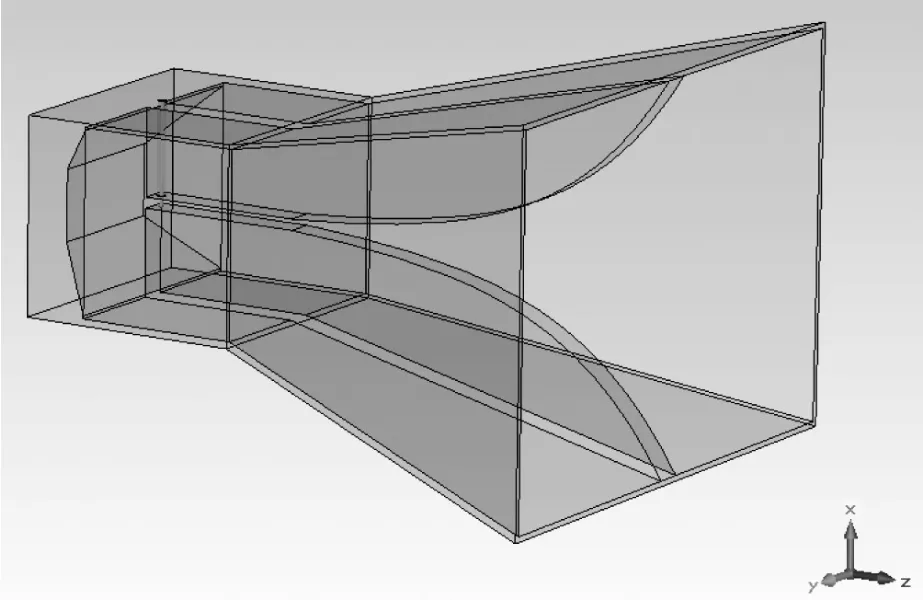
图4 双脊喇叭天线模型
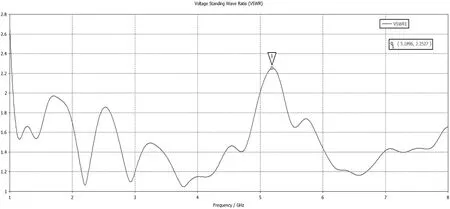
图5 初始模型仿真的VSWR曲线
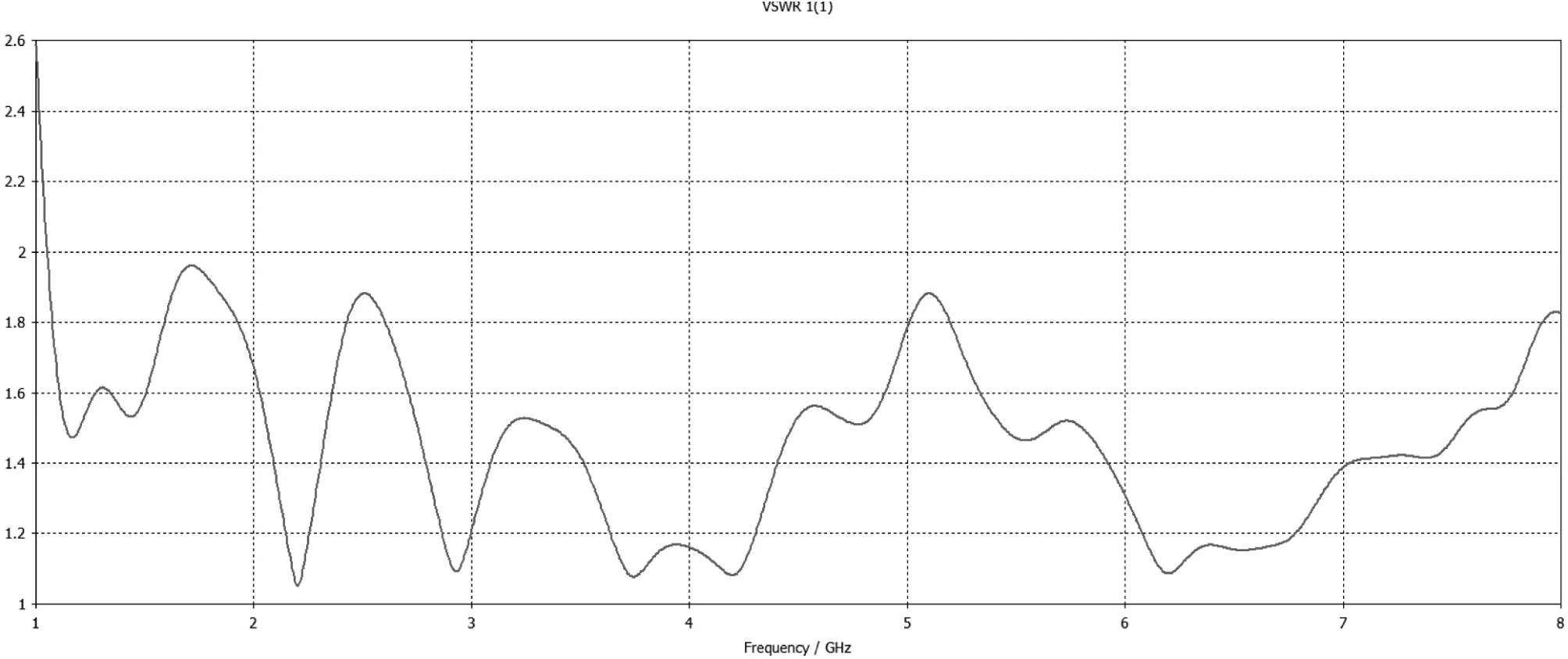
图6 VSWR的最终优化的结果
分析波导部分的窄边长度b对驻波比的仿真影响曲线,从结果中可以看出,b的变化对驻波比影响较大,随着b的增大,位于5.2 GHz处的一个峰值逐渐降低,但当b增大到76 mm时,在高频8 GHz附近驻波比出现了明显的上升。
分析扫描双脊间距s对驻波比的仿真影响曲线,驻波比对于s的变化非常敏感,当s等于1 mm时能够得到最优驻波比,后面我们从天线内部的电场分布也会说明为什么s对于天线的影响较大。
分析喇叭口径的窄边长度a1对驻波比的仿真影响曲线,从结果中可以看出,随着a1的增大,整个曲线向低频移动,这是因为口径长度越大,对应的工作频率越低,所以整个天线是驻波比曲线往低频移动。
分析喇叭口径的宽边长度b1对驻波比的仿真影响曲线,从结果中可以看出,在2 GHz以后,b1的变化对天线的驻波比几乎没有影响。在1~2 GHz之间,b1越大,则在1 GHz处明显改善,但在2 GHz处会变差。在b1=200 mm时,可得到良好的折中值。
通过a、b、s、a1、b1多参数的分别扫描,给出了各个参数的初步取值范围,然后同时优化这些参数:将各个参数设置成相同的权值,将驻波比设计成优化目标,最后得到最理想的驻波比。这种多参数同时优化的方法考虑了各个参数的互相影响,从而保证最理想的系统优化值。CST最终优化的参数:波导部分宽边为a=90,窄边长b=68 mm,波导长度为80 mm,双脊间距s=1 mm,脊宽为10 mm,脊曲线变量C=0.01,喇叭口径宽边为w=200 mm,窄边为h=140 mm,喇叭部分长度为150 mm。最终参数仿真出来的驻波比曲线如图6所示,驻波比在1.05~8 GHz都能保持在2以下,在1~1.05 GHz这个频段内略高于2,这主要是尺寸限制的原因,造成截止频率略微偏移,这个设计误差是可以接受的范围。
为了分析天线的工作模式,图7给出了各个频率对应的电场分布图,从图中可以看出,对应的各个频点都出现了明显的TE模式,而未出现TM模式,这也达到了我们的设计预期。同时,从电场图中可以看到,在双脊之间有比较强的电场,这也解释了为什么我们在调整双脊间距时,驻波比变化会那么大。
图8给出了各个频率对应的辐射方向图,从图中可以看出,各个频点的最大增益都出现在+Z方向,这符合我们的设计预期。在1 GHz、3 GHz、5 GHz、8 GHz处的增益分别为 6.8 dBi、10.7 dBi、12.5 dBi、16.7 dBi。虽然在8 GHz时,最大增益旁边出现了两个小的凹陷(增益下降),但最大增益仍然在+Z处,这就不影响电磁兼容测试的使用。
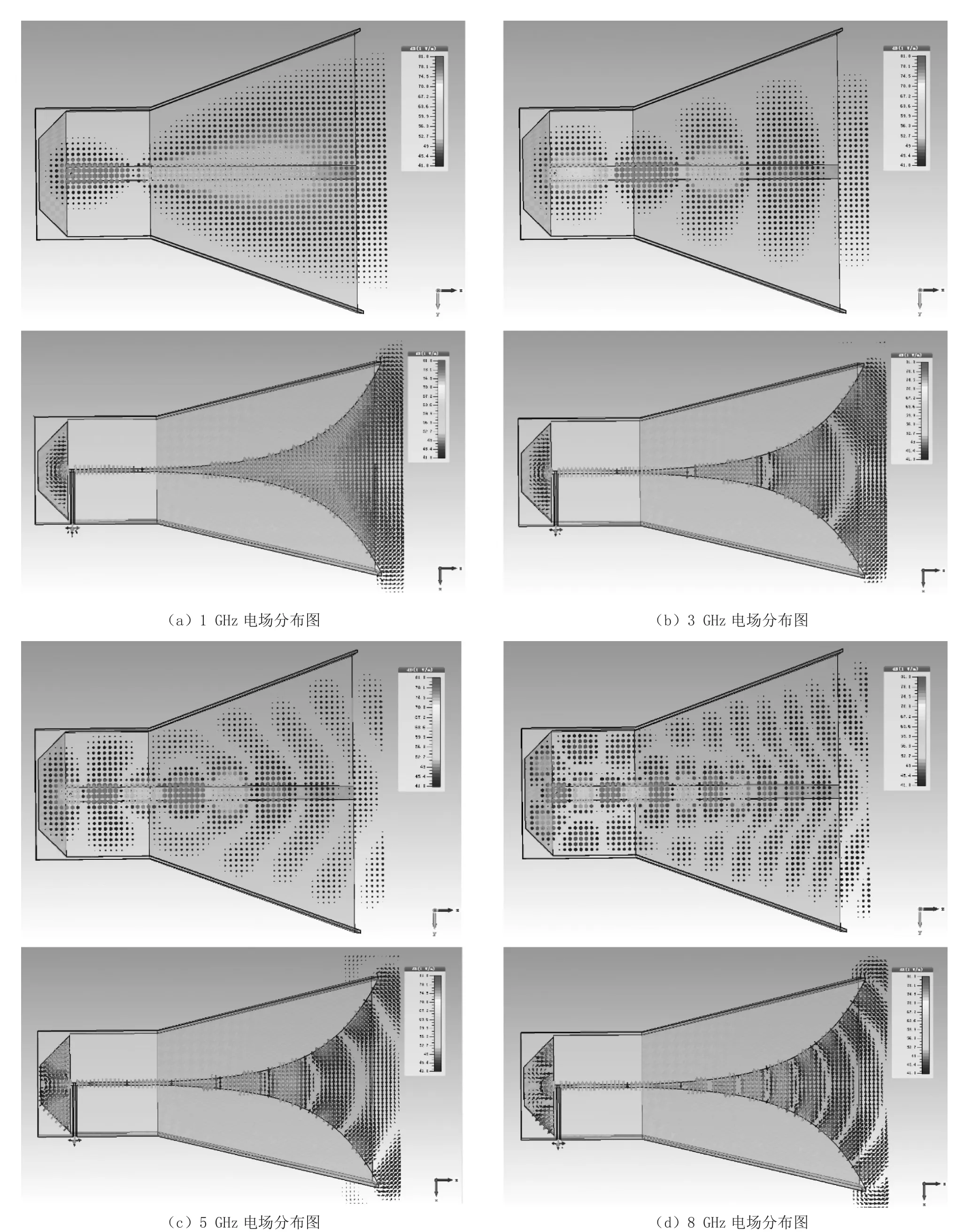
图7 各个频率对应的电场分布图
综上所述,本章所设计的双脊喇叭天线符合矩形波导的TE模式,辐射符合角锥喇叭天线特性,在1~8 GHz频段内的驻波比、增益、辐射方向图都满足电磁兼容测试的需求,这种工作与宽频段的高增益天线有较高的实用价值。
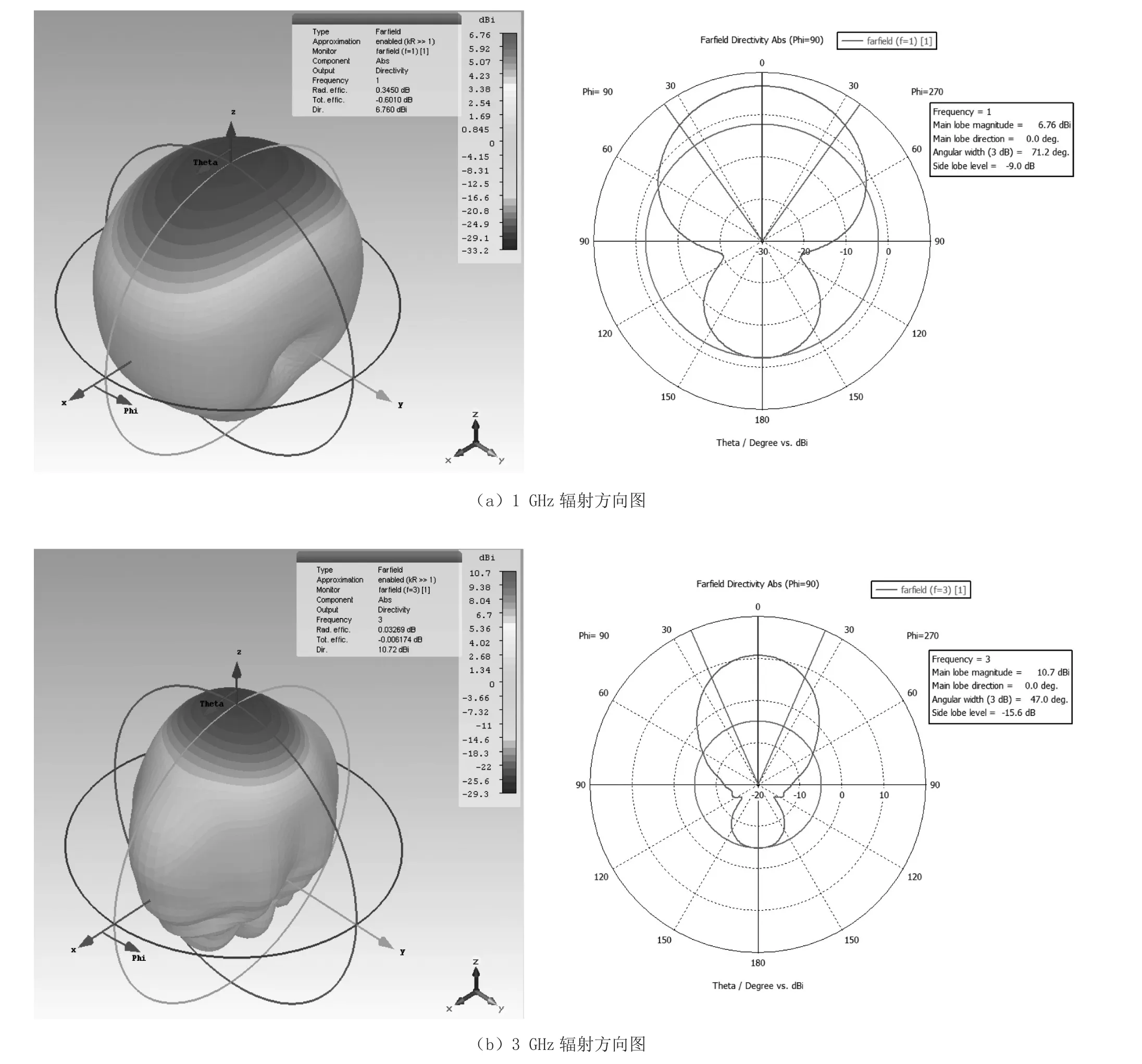
图8 最终的辐射方向图
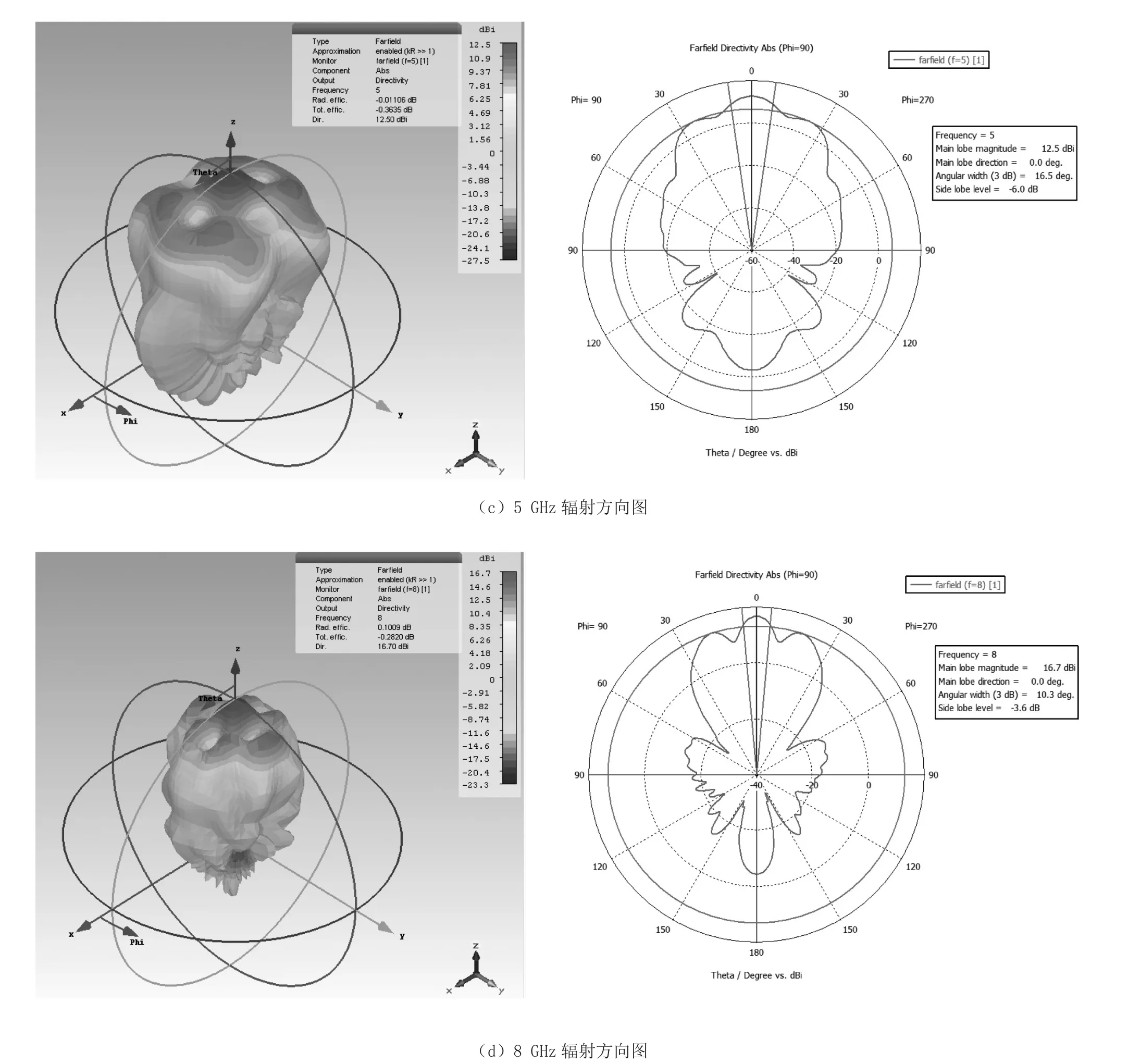
图8 最终的辐射方向图
