应用Squeeze算法实现地震数据高效压缩

高 潇，张 伟，徐锦承，杨 辉，邵理阳，潘 权，宋章启

(1.中国科学技术大学 地球和空间科学学院，合肥 230000;2.南方科技大学 a.地球与空间科学系，b.电子与电气工程系，c.创新创业学院，深圳 518055)

0 引言

随着地震勘探规模的扩大，海量的地震数据需要被存储以供后期处理使用。尽管这个问题可以通过使用大容量的地震存储设备来解决，但是在实际处理中计算机的IO瓶颈又会限制处理速度，从而出现计算机IO能力与计算能力不匹配的现象。因此，将数据压缩之后保存，不仅能解决海量数据的存储问题，同时也能减轻IO负担，加快处理速度。

目前的数据压缩方法通常被分为两大类：①无损压缩;②有损压缩。对于无损压缩，数据压缩之后能完全恢复，不丢失任何信息，但随之而来的问题就是无法实现较高的压缩率。而有损压缩的压缩过程一般都分为变换-量化-编码三个过程[1-3]。相对无损压缩，有损压缩增加了变换、量化这两个步骤：变换可以有效地消除数据间的相关性，数据间相关性越大，数据的冗余度就越大；量化是将主要变换系数和次要变换系数区分开来，主要系数包含数据的概貌部分，是必须保留的，否则无法重构数据，次要系数重构数据的细节部分，是对重构数据质量的进一步提高，有损压缩就是通过舍弃部分次要系数来实现高压缩率的。虽然压缩前、后数据会出现一些差异，但通过设置合适的压缩参数，这些差异就会比较微弱，并且丢失的是数据中的非主要信息，在很多实际应用中这种误差是完全可以忽略的。

对于地震数据的压缩算法研究，早期开始于传统的无损压缩算法(如Huffman编码压缩[4]，LZ77编码压缩[5]或LZW编码压缩[6]等)，之后为了规范地震数据压缩后的交换格式，国际数字地震台网联合会(The International Federation of Digital Seismograph Networks, FDSN)，将Steim压缩算法确定为地震数据交换标准格式的核心算法，Steim算法目前常用的主要是两种:①SEED数据格式所采用的Steim1算法;②miniSEED数据格式所采用的Steim2 算法，但这些无损压缩算法用于地震数据能实现的最大压缩率有限，不能满足实际海量数据的存储需求。而有损压缩算法根据研究目的不同，用户可以自行设定压缩参数从而使压缩率达到10乃至超过100[7-10]。正因为如此，在过去几十年，许多地球物理学家都致力于寻找一种高效的地震数据有损压缩算法。当前比较流行的地震数据压缩算法大都是基于变换的压缩算法，如Candes等[11]提出的多尺度、多方向的各向异性变换方法——Curvelet变换；Pennec等[12]提出的Bandelet变换；Guo等[13]提出的Shearlet变换以及Fomel等[14]提出的Seislet变换等，而目前使用最多的两个典型代表就是：离散余弦变换[9,15-18]和小波变换[6,10,19-26]。

Ahmed[15]在JPEG图像压缩算法中首次提出了离散余弦变换的概念；Spanias[17]对比了四种基于变换的压缩方法对地震数据压缩的效果，结果表明，DCT是最健壮且有效的；刘财[18]在DCT的基础上，将游程编码算法引入到了地震数据压缩中，测试显示这种技术对层间相似性较强的数据具有不错的压缩效果；Dalmau[9]为了解决磁盘的IO限制，将DCT应用到了时间域逆时偏移的互相关处理中。然而，由于该算法自身的特性，即将数据分块处理，当实现较高的压缩率时，解压得到的数据块之间存在明显的边界，这个即是所谓的“块状效应”[7]。小波变换是一种用于图像层次分解的数学工具[27]。相比于离散余弦变换,由于小波变换引入了不同的母小波，这些母小波可以通过扩张或收缩以及平移来构造最适合的子波，从而更易于获得最佳的压缩效果。另外，由于不需要对数据进行分块处理，从而使小波变换压缩得到的数据即使在高压缩率的情况下，也不会产生”块状效应”[28]。唐向宏等[29]以二维地震数据具有较强的分频带特性为切入点，提出了一种利用M带小波变换进行压缩的算法，该算法能在保证重建数据精度满足后续处理的前提下，获得10～20的压缩比；徐锋涛等[30]提出了一种基于嵌入式零树小波编码(EZW)的地震数据压缩算法，其首先对地震数据进行二维小波变换，之后利用系数之间的相关性对变换后的系数采用嵌入式零树小波进行编码，最后使用自适应算术编码对量化后的系数进行无损熵编码。但是小波变换不能很好地表示数据中的震荡模式，而地震数据又恰好具备这种特性[7]。

近年来，除了上述的一些经典地震数据压缩方法外，一些新的方法也被提出。耿瑜等[31]将Dreamlet变换应用到了地震数据压缩中；Dreamlet变换中利用到了局部余弦基和频散关系，研究结果表明，对于地震数据压缩而言，Dreamlet变换比Curvelet变换具有更好的性能；Boehm[32]提出了一组专门针对全波形反演中伴随状态方法的波场压缩策略，包含粗空间网格重新插值，自适应选择多项式阶数和自适应选择浮点数精度这三个步骤。尽管这种压缩方法能获得比较理想的压缩率，但它其中的一个压缩策略是专门针对谱元法设计的，因此如果要在其他方法中使用(有限差分法)，就需要额外的适配工作。Lindstrom[10]将zfp压缩算法(zfp算法是一个开源的用于压缩浮点数组的C/C++函数库，由劳伦斯利弗莫尔国家实验室的Peter Lindstrom, Markus Salasoo和Matt Larsen开发并维护)用到了三维全空间波形层析成像的散射积分计算实现中，从而大幅减少了数据存储量并显著提高了IO性能；陈祖斌等[33]将压缩感知算法应用到了地震数据压缩重构中，该方案在下机位实时使用混沌伯努利测量矩阵压缩小波变换后的系数，同时在上机位结合使用贝叶斯小波树结构压缩感知重构算法和马尔科夫链蒙特卡洛推理对数据进行解压；实际数据测试表明这种方法具有不错的压缩效果；Nuha[34]以神经网络研究为基础，提出了一种适用于检波器地震数据的实时压缩算法，与常规方法相比，这种方法在压缩率和重构数据质量上都要更优。

Squeeze压缩算法(SZ)，是由美国阿贡国家实验室的Di和Cappello[35-36]开发维护的一种误差约束的有损压缩算法，即数据在压缩过程中会严格遵循用户定义的误差。SZ最初的研发目的是为了提升高性能计算中的check-point性能以及数据的后续处理效率。SZ压缩算法相比之前传统的压缩算法，具有压缩性能高、扩展性好以及移植性佳的优点，并且时间复杂度只有O(N)。为了对比SZ压缩算法和其他高性能计算中常用的压缩算法之间的性能差异，Di和Cappello以及Tao对13个涵盖了各个学科领域的高性能计算应用进行了测试[35-38]。实验结果表明对任何一个HPC应用得到的数据集进行压缩，SZ的性能都是最佳的。此外SZ支持多种语言，包括C、Fortran以及Java。

SZ的压缩实现十分简洁，只需在代码中添加几行压缩函数调用，就能实现数据的高效压缩存储。但目前还没有SZ在地震数据压缩中的相关工作。笔者首次将SZ压缩算法引入到地震数据压缩中，首先对Squeeze的算法实现进行阐述，之后对其与实际工作结合的编码进行简单示例，接着通过三个测试案例比较Squeeze算法与DCT压缩和Dreamlet压缩的性能差异，最后给出相应的结论。

1 Squeeze算法的原理

SZ的算法实现包括三个步骤：①基于多层和多维数据的预测模型；②自适应误差约束量化；③熵编码模型。

1.1 多维和多层预测模型

与传统基于变换的压缩方法不同，SZ基于多项式预测。SZ算法的早期版本[35]使用的是一维预测算法，包括常量、线性以及二次预测模型。之后的版本[37-38]将预测模型改进成了多维，从数学意义上来说，称之为Lorenzo预测，这一改变使数据的预测命中率相比之前有了显著提高。

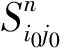
图1 二维多层预测模型示例

k1,k2≤n}{i0,j0}

(1)

V(i0-k1,j0-k2)

(2)

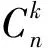
f(i0,j0)=2V(i0-1,j0)+2V(i0,j0-1)-

4V(i0-1,j0-1)-V(i0-2,j0)-

V(i0,j0-2)+2V(i0-2,j0-1)+

2V(i0-1,j0-2)-V(i0-2,j0-2)

(3)

类似推导可以得到多维多层的预测模型，

V(x1-k1,…,xd-kd)

(4)

其中：d为预测模型中数据集的维度；n为预测所用的层数。对于一个给定的数据集，参数d是固定的，但是n是可变的。从一方面来说，增加预测层数可以获得比较好的预测精度，但从另一方面而言，使用的层数越多，引入的不相关信息也越多，从而在某种程度上也会降低预测精度。因此，压缩性能的好坏与预测层数n的选择有很大关系，需要针对不同问题测试选择最优的n值。

1.2 自适应误差约束量化

经过上面的多维和多层预测之后，需要将预测值在误差约束条件下进行量化。SZ算法的误差约束是指允许用户通过配置压缩参数来对压缩结果的误差进行控制。在SZ中，用户可以选择三种误差约束方式中的一种用于当前的工作：

1)绝对误差约束(ABS)。每一个数据点的压缩误差都被限定在同一个最大允许误差范围(Max Error, ME)内。例如，设定误差约束ebabs=0.000 1，数据点的原始值为V，那么该点解压之后的值必须在[V-0.000 1,V+0.000 1]范围内。

2)相对误差约束(REL)。也称为基于数据范围的相对误差约束，会在考虑数据集范围的基础上，得到一个误差值。例如，设定ebrel=0.01，原始数据集是[100，101，102，…，108，109，110]，那么，由于数据集范围是110-100=10，每一个数据点的最大误差就是10*0.01=0.1。

3)逐点相对误差约束(PW_REL)。类似REL，但是它不考虑整体的数据范围，而是将当前点的数值作为一个数据范围。例如，设定ebpw=0.01，那么对每一个点的数据ME就是0.01*V。

这三种压缩设置都有各自的优缺点，实际处理中选用哪一种需要结合具体的研究问题而定，并且用户可以自行调优以获得最适合的压缩方式。在本文中，由于地震数据变化范围较大，使用绝对误差约束方式和逐点相对误差方式都不能获得比较好的压缩效果，因此我们使用第二种误差约束——相对误差约束(REL)进行压缩。

选定误差约束方式后，就可以根据相应的误差约束条件计算出最大允许误差ME值，之后的量化操作以ME值为基础，其具体又可以分为两个过程。

1)首先在第一步多层预测的基础上，获得当前点的预测值，在算法中称之为“第一阶段预测值”，如图2中的红点所示。设定量化编码位数为m，则总共可支持2m-1个量化编码(编码“0”有其他用途)。以“第一阶段预测值”为中心，向两端各增/减1倍ME值，从而获得一个“基础预测范围”。之后以该“基础预测范围”为单位(2*ME)，向上/向下各线性延拓次，从而共获得2m-1个“预测范围”，从值最小的预测范围开始以“1”为起始序号编码，相应的编码值如图2右半部分所示。

图2 在误差约束下的量化过程示意图

2)当真实值落入某一个预测范围内，就用该预测范围的中心值表示，称其为“第二阶段预测值”。不难看出，“第二阶段预测值”与真实值(图2中蓝点)之间的误差一定小于ME。在实际压缩中，保存的是“第二阶段预测值”所在区间对应的编码值。

若当前处理点的真实值能落入到扩展出来的间隔内，SZ算法就标记该点是可预测的，同时用相应的“第二阶段预测值”表示解压缩后的数值，用相应的量化编码表示压缩的数据。但是如果原始值不能落入扩展出来的间隔内，那么SZ算法将标记这个点是不可预测的，并将该点的量化编码标记为“0”，之后采用另外一套压缩算法进行处理——二进制表示分析压缩算法。如前所述，这个量化过程共需要m位二进制来编码所有的数据。SZ算法允许用户自定义m的大小，若在压缩过程中不显式指定，算法自身也会根据数据集自适应地选择合适的m值进行编码。

1.3 熵编码

经过以上预测和量化两个步骤，数据转换成了采用位数有限的量化编码表示，实现了有损压缩。为了进一步提高压缩效果，SZ算法在最后步骤引入了熵编码。这是一种无损压缩算法，基本思想就是将出现次数越多的数据项用位数越少的编码项代替。在具体实现中，使用的是经过优化的哈夫曼编码算法。

在当前常见的压缩算法中，都会使用熵编码来提高压缩率，笔者在之后数值测试部分所使用的DCT和Dreamelt压缩算法，在最后的操作步骤也使用了标准JPEG算法所采用的游程编码和哈夫曼编码来实现熵编码操作。

2 在地震波模拟中的应用

Squeeze算法相对于其他压缩算法而言，简单易用是其一个显著特点。由于底层实现已经完全封装好，只需要调用相应的接口就能实现数据的高效压缩，地球物理学家不需要花费很多精力去学习压缩算法原理，可以将精力集中在要解决的科学问题上。

将Squeeze算法与地震波正演模拟程序相结合，其总体实现流程如表1所示(以Fortran代码为例)。从表1中可以看出，只需要在工作中添加几行代码，就能实现一个比较理想的压缩方案。

表1 Squeeze算法与地震波模拟程序结合示例

3 数值测试

对SZ的压缩效果进行测试，研究压缩中一些典型参数的取值方法。压缩效果主要通过压缩率(CR)和压缩误差(CE)来进行衡量，定义如下：

CR=原始数据大小/压缩数据大小

(5)

CE=abs(原始数据数值-解压数据数值)

(6)

3.1 二维地震记录压缩

笔者先对SZ在地震记录数据上的压缩效果进行测试，所用数据是叠后二维SEG-EAGE盐丘的地震记录数据(图3)。同时，与离散余弦变换压缩和Dreamlet变换压缩进行效果对比。与SZ压缩不同，基于变换的DCT压缩和Dreamlet压缩不是误差约束的，它们都是通过控制变换系数的保留比例来实现数据压缩。一般保留比例用参数rt表示，具体实现为：原始数据经过变换后将获得变换后的系数，如果没丢失其中的系数，数据能够完全变换回原始数据，但为了获得较高的压缩性能，势必需要丢弃部分系数，定义绝对值最大的变换系数和rt的乘积作为阈值，当系数的绝对值小于这个阈值时，就会被抹零。

图3 2维SEG-EAGE叠后盐丘地震记录数据

测试了这三种方法在不同的压缩设置下的压缩效果，如表2所示。同时为了衡量数据集的平均压缩误差大小，引入了峰值信噪比系数(Peak Signal-to-Noise Ratio,PSNR)这一指标，数学定义为式(7)。

表2 不同压缩设置下的离散余弦变换，Dreamlet变换和SZ的压缩率以及PSNR

(7)

其中：Rx是数据范围，Rx=xmax-xmin；rmse表示均方根误差，定义为式(8)。

(8)

一般来说，rmse数值越大或PSNR数值越小就表示压缩误差越大，反之亦然。图4给出了这三种方法压缩率和PSNR之间的关系曲线(部分)。从图4中可以清楚地看到，在相同压缩率的情况下，Dreamlet压缩的PSNR最小，其次是DCT，SZ算法的PNSR最大，从而说明其误差相对较小。图5是三种方法在压缩率接近的情况下，解压缩之后的数据，其中图5(a)是压缩设置为rt=5.0E-4情况下的DCT解压缩结果，其压缩率CR=9.578；图5(b)是压缩设置为rt=3.0E-2情况下的Dreamlet解压缩结果，其压缩率CR=9.710；图5(c)是压缩设置为rel=5.0E-5情况下的SZ解压缩结果，其压缩率为CR=9.778。从图5中可以看出，Dreamlet变换的解压缩结果相对较差，在600左部和1 200右部丢失了许多重要的细节信息，相比之下，DCT和SZ的解压缩结果要好很多，且在视觉上整体差异不大。

图4 DCT, Dreamlet和SZ三种压缩方法压缩率与PSNR之间的关系

为了更加确切地比较三者的差异大小，在图5的基础上，获得了它们各自的压缩误差，如图6所示。其中DCT的最大压缩误差绝对值为0.002 679，Dreamlet压缩为0.191 113，而SZ压缩为0.000 033，这比DCT压缩误差小2个数量级，比Dreamlet压缩误差小4个数量级。为了对比明显，将图6的显示刻度范围都限定在[-1.5*10-3,1.5*10-3]，从中可以看出，在压缩率为9.5左右时，SZ和DCT的压缩误差相对Dreamelet方法都比较小，并且SZ更略优一些。

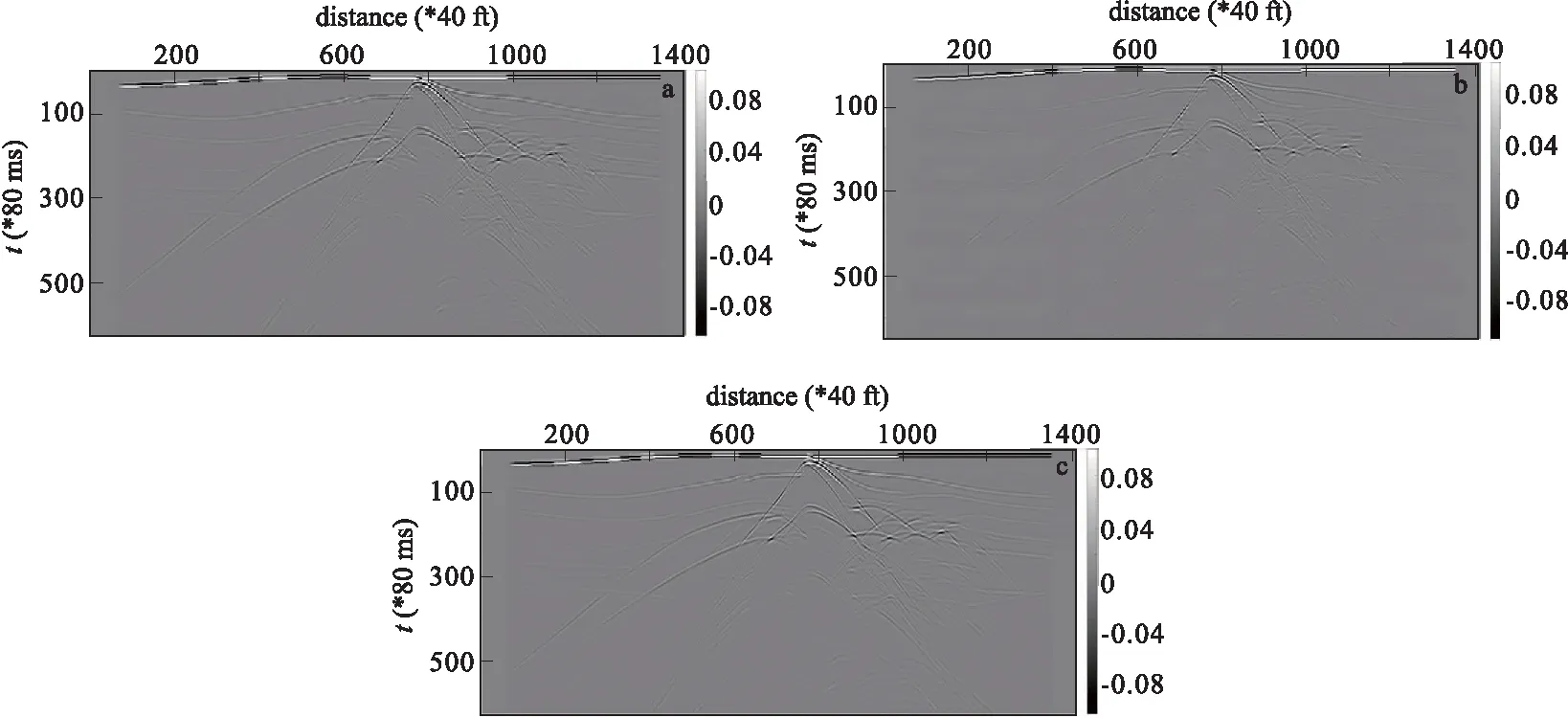
图5 DCT、Dreamlet和Squeeze的压缩数据对比

图6 DCT、Dreamlet和Squeeze的压缩误差对比

3.2 三维实际地震道集记录压缩

我们采用实际原始道集记录对Squeeze算法的压缩能力进行测试，同样也与Dreamlet和DCT压缩算法对比测试结果。测试使用的道集记录数据共有432炮，每一炮都有12条测线接收数据，每条测线有检波器120个，间距为50 m，单个检波器记录时间为6 s,采样间隔为4 ms。

表3展示了压缩率约为8.5时，三种方法的压缩参数设置。为了对比数据误差，我们在这里随机选择第27炮的道集数据进行分析，图7是其所有测线原始道集记录，图8分别是DCT、Dreamlet和SZ算法的压缩重构结果。从图8中可以直观地看出，对于DCT和Dreamlet压缩，它们的重构数据在数据采集的初始阶段(例如t<500 ms)以及末尾阶段(例如t>4 000 ms)的误差比较大，同时由于这两个算法都是分块操作的，因此重构得到的数据中会有比较明显的分块特征，误差呈现比较明显的块状分布；SZ重构得到的数据误差除了在数据采集的初始阶段会有比较明显的误差外，之后阶段都能比较好地保留原始数据特征。图9是它们三种方法的重构误差对比，DCT和Dreamlet的误差比较接近，它们在t>1 600 ms区域丢失了比较多的细节信息，而SZ误差相对小很多，未见有明显的细节信息丢失，从而验证了SZ算法用于原始道集记录压缩的可行性。

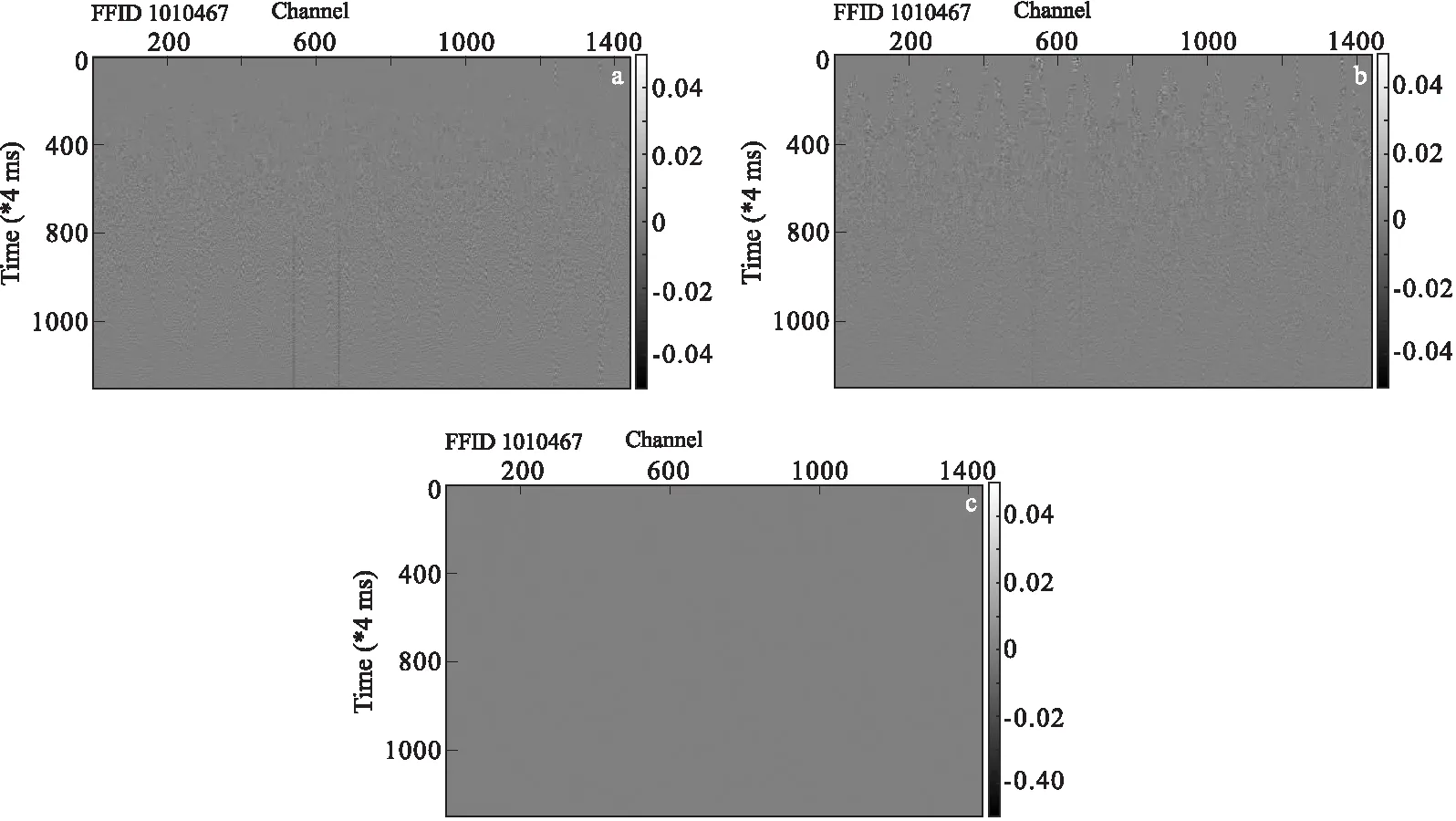
图9 压缩率约为8.5DCT、Dreamlet和Squeeze的重构误差对比

表3 压缩率约为8.5时的离散余弦变换、Dreamlet变换和Squeeze算法的压缩设置

图7 第27炮的所有测线原始地震记录数据(AGC时间窗=500 ms)

3.3 全空间波场数据压缩测试

为了进一步测试Squeeze算法对波场数据的压缩效果，使用有限差分方法[39-41]对Marmousi模型(部分)进行正演波场模拟，之后对获得的全空间波场数据进行压缩。具体操作为每模拟一个时间步，就将相应的全空间三维波场数据压缩并输出。为了对比压缩效果，同样使用DCT，Dreamlet和SZ三种算法对数据进行操作。正演模拟相关参数如表4所示，相应的Marmousi模型(切面)如图10所示，实际使用的三维模型是该切面沿着y方向扩展得到的。

表4 Marmousi模型的正演模拟参数设置

图10 Marmousi模型(部分)的P波速度切面(y=250 m)

在对三种压缩方法各自测试了不同的压缩设置后，获得了三种方法压缩率大致相同的情况，如表5所列。

表5 相近压缩率下的离散余弦变换，Dreamlet变换和Squeeze算法的压缩设置

为了对比压缩效果，使用正应力Txx分量在t=0.6 s、y=250 m处的波场快照进行分析。原始波场快照如图11所示，相应的压缩之后的数据如图12所示，从图12中可以明显看出，三种方法的压缩都没有使原始数据发生比较大的差异。图13则展示了具体的细节差异。从图13中可以直观看出，Dreamlet的压缩误差相对较大，其次是DCT，Squeeze的误差相对较小。这个结果同前面测试相同，表明Squeeze算法对地震波场数据压缩也有比较好的适用性。

图11 正应力Txx分量在t=0.6 s、y=250 m处的原始数据波场快照

图12 压缩率相近DCT、Dreamlet和Squeeze的波场快照压缩数据对比的原始数据波场快照

图13 压缩率相近DCT、Dreamlet和Squeeze的波场快照压缩误差对比

基于变换的DCT和Dreamlet压缩算法由于在变换过程中涉及到数据的多维变换操作，其中包含大量的指数以及乘法运算，其压缩过程的时间复杂度不是O(N)，而SZ算法的时间复杂度只有O(N)，并且其预测步骤也只有简单的一些加法和乘法运算(式(3))，量化步骤也没有涉及到复杂运算，因此SZ的计算量以及计算效率从理论上来说会比前两种压缩方法好。实际测试结果也验证了这一点，在如上4 000时间步正演波场压缩过程中，DCT平均压缩耗时为0.42 s/步，Dreamlet平均压缩耗时为0.45 s/步，而SZ平均压缩耗时为0.31 s/步。对于解压缩过程，DCT平均0.29 s/步，Dreamlet平均0.32 s/步，SZ平均0.19 s/步，这说明利用SZ进行数据压缩的处理效率是相对较高的。

为了探究由于压缩造成的误差对地震波场研究的影响，我们在此以敏感核[42]计算为例进行分析，因为敏感核计算需要使用到波场数据。图14是利用原始地震波场数据计算得到的振幅衰减敏感核，图15分别是利用DCT、Dreamlet以及SZ算法压缩得到的波场数据计算得到的敏感核，从图15中可以看出，三种方法得到的敏感核形态基本与原始数据计算得到的相同，图16分别是它们各自的误差，从图16中可以看出，DCT和Dreamlet的误差比较接近，但是SZ的误差相对它们两个要更小一些。这说明SZ能在实现较高压缩率的同时保证后续处理的数据精度。

图14 原始波场数据计算得到的振幅衰减敏感核

图15 压缩率相近DCT、Dreamlet和Squeeze压缩数据计算得到的振幅衰减敏感核对比

图16 压缩率相近DCT、Dreamlet和Squeeze压缩数据计算得到的振幅衰减敏感核误差对比

4 结论

笔者对Squeeze算法原理进行了简要概述，并将其应用到了叠后数据，实际道集记录数据和波场数据的压缩实现中。通过与基于变换的离散余弦变换压缩和Dreamlet变换压缩的测试结果对比，SZ算法在相同压缩率的前提下，可以在较大程度上保留原始数据特征，实现较小的压缩误差，同时对后续处理造成的误差影响也是相对较小的，并且SZ算法的压缩和解压缩时间开销也很低。另外，SZ算法由于使用的便捷性，其在实际工作中的编码复杂度在这三种方法中也是较为简单的。