GNSS模糊度整数估计方法图形可视化软件设计与应用分析

吴汤婷,刘丽晶,赵宝贵,卢立果

(1. 东华理工大学 江西省数字国土重点实验室,江西 南昌 330013;2. 东华理工大学 测绘工程学院,江西 南昌 330013)

0 引 言

载波相位整周模糊度的快速准确解算是全球卫星导航系统(GNSS)实时高精度动态定位的关键问题,错误的整周模糊度将导致分米级甚至更大的定位偏差[1-4],而模糊度解算的核心在于模糊度浮点解的整数估计. 常用的三类模糊度整数估计方法包括:整数取整、整数序贯取整和整数最小二乘[5-10]. 尽管从理论上三类整数估计算法较容易被实现,且已有公开软件LAMBDA3.0提供三类模糊度整数估计功能[11]. 但是单纯地根据数学原理直接估计出整周模糊度,而对模糊度由实数空间映射到整数空间的过程缺乏直观的认知,不利于对三类估计理论的深入理解. 为更好地解释这三类整数估计过程,文献[5-6]采用归整域构建了模糊度实数域与整数域之间的几何关系,文献[7]进一步采用蒙特卡洛模拟了不同精度下模糊度的浮点解与归整域之间的几何关系,用以说明三类估计方法的性能. 尽管三类估计方法几何原理清晰、图形直观,便于对三类整数估计原理的理解,但是实现过程较复杂,且目前尚未有公开软件提供这类功能的演示. 因此,本文通过研究三类估计方法的一般理论表达式,基于MATLAB GUI设计了一套三类估计方法二维几何图形构建的可视化分析软件,实现对三类估计方法的归整域、映射图和蒙特卡洛模拟及成功率计算等分析,为后续相关研究提供参考和帮助.

1 基本理论

1.1 归整域

Sz={x∈Rn|z=F(x)},∀z∈Zn,

(1)

式中,z为整数向量.

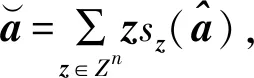
(2)

式中:sz(·)为指示函数,有

1.2 整数取整

整数取整(IR)估计是将模糊度浮点解向量的每个元素直接取整到最近的整数向量. 因此,IR估计不考虑模糊度分量间的相关性,其表达式为

(3)

式中，[·]表示对元素进行取整运算；n=1, 2, 3, ….

由于IR是将模糊度浮点解直接归整到最近的整数上,浮点解与整数解的差异值不超过0.5. 因此,IR估计的归整域一般表达式为[6]

i=1,2…,n, ∀z∈Zn,

(4)

式中，ci为第i个元素为1的单位坐标向量.

1.3 整数序贯取整

(5)

式中:

(6)

式中，lk,i为LTDL分解的单位下三角矩阵L的元素.

IB估计是将浮点解的条件期望取整到距其最近的整数,条件期望与取整的整数解的差异值不超过0.5. 因此,IB估计的归整域一般表达式为[6]

(7)

1.4 整数最小二乘

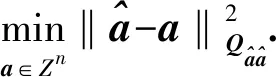
(8)

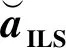
(9)

因此,ILS归整域一般表达式为[5]

∀z,u∈Zn,z≠u,

(10)

式中:x为浮点解;z为ILS解;u为任一整数向量.

式(10)可以进一步简化为

(11)

式中:c=u-z.

由式(11)可知,ILS归整域是由多个平面围成的空间,且平面数取决于模糊度次优解个数,模糊度次优解个数区间为[2n, 2n+1-2]．

2 三类整数估计方法归整域演示软件设计

图1为三类整数估计方法图形可视化软件功能结构图，图2为三类整数估计图形可视化软件界面.

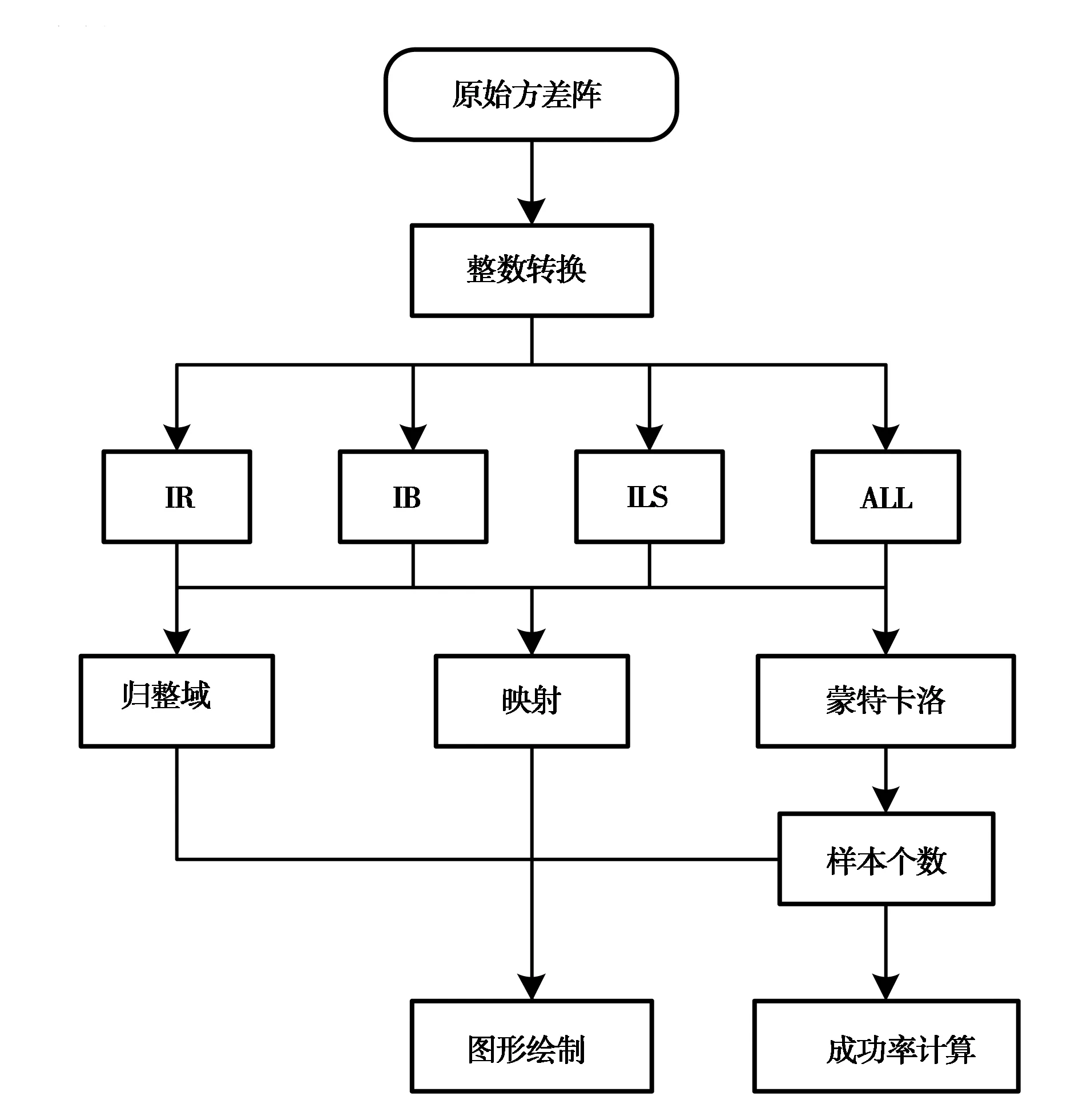
图1 三类整数估计方法图形可视化软件功能结构图.

图2 三类整数估计方法图形可视化软件界面.

3 软件测试与分析

3.1 归整域图

图3为绘制的IR归整域图.从图中可以看到IR的二维归整域是由规则的正四边形构成的实数空间. 分析其原因为IR估计仅与浮点解有关,取整过程可以看作是浮点解的四舍五入,因此对于二维模糊度来说,其归整域是一个规则的正四边形,且整数转换前后不改变其形状.

图3 IR归整域图形

图4 IB转换前后归整域图形及其形状变化图

图4为绘制的IB整数转换前后归整域及其变化图.由图可见IB的归整域为一个平行四边形,转换后的形状相对于转换前更接近正四边形. 分析其原因为基于LTDL分解的IB估计是由后到前的顺序进行序贯取整,因此对于二维模糊度向量来说,第一个估计的模糊度分量(即Y轴方向)是按照直接取整获得的,第二个估计的模糊度分量(即X轴方向)是基于式(4)序贯取整得到的,其取整范围受模糊度分量间的相关性影响,但是每一个归整域在X轴方向的边界范围大小仍为1,此时归整域为平行四边形. 当模糊度分量不存在相关性时,IB估计等同于IR估计,此时IB的归整域简化为正四边形. 由于整数转换的中间过程可以有效地降低模糊度分量间的相关性,因此转换后的形状将更接近正四边形.

图5为绘制的ILS转换前后归整域及其形状变化图.由图可以看到转换前由于模糊度分量间相关性很大,ILS的归整域是一个狭长的凸六边形,转换后的归整域为一个比较规则的凸六边形. 分析其原因为ILS是基于最小二乘搜索获得最优解(即ILS解),而对于同一个最优解当浮点解选取不同时将会对应不同的次优解,由式(10)可知其归整域的构建取决于次优解和最优解之间的线性关系. 对于二维模糊度向量来说,通常根据浮点解的选取不同最优解对应六个次优解,此时归整域为六条直线构成的交叉区间. 需要说明的是,当模糊度分量线性无关时,ILS估计等同于IR估计,此时归整域简化为正四边形. 对于原始的模糊度向量,由于模糊度分量间的相关性很大,此时归整域是一个狭长的凸六边形;而整数转换的中间过程可以有效地降低模糊度分量间的相关性,此时转换后的形状将朝着接近正四边形的方向变化.

图5 ILS转换前后归整域图形及其形状变化图

3.2 映射图

图6为整数转换后三类估计方法映射图.其中,模糊度真值假定为零向量. 由图可知,每个整数向量对应唯一的归整域,且各归整域之间互不重叠,当采用IR、IB和ILS估计时,浮点解处于零向量所在的归整域才能获得正确值,反之则会错误固定. 因此,三类估计方法的模糊度浮点解和固定解在归整域内满足“多对一”的映射关系.

图6 整数转换后三类估计方法映射图(绿色点为真值，红色点为错误值)

3.3 蒙特卡洛模拟浮点解图

图7为蒙特卡洛模拟生成的浮点解与三类归整域的关系图.其中,模拟样本数为10 000. 由图可见,整数转换前浮点解分布在一个倾斜的扁形椭圆空间内,整数转换后浮点解分布在一个近似圆形的椭圆空间内,主要是由于整数转换通过降低模糊度相关性实现了椭球的压缩. 在三类归整域与浮点解空间分布的关系方面,ILS在整数转换前后归整域均与浮点解分布形状保持最大程度的吻合,IB次之,IR最差,且IB和IR与整数转换直接相关,整数转换有利于增大二者的吻合程度.

3.4 成功率计算

表1所示为整数转换前后三类方法模糊度正确估计的概率.其中,成功率=落在归整域内样本数/总样本数,为保证成功率统计的准确性尽量不受蒙特卡洛模拟样本个数的影响,样本数设定为10 000 000. 由表1可知，整数转换前,IR和IB的成功率远低于ILS,整数转换后IR和IB的成功率得以较大程度地提高,ILS成功率不受整数转换的影响,三类方法模糊度估计的成功率大小满足不等关系:PS,IR≤PS,IB≤PS,ILS,统计结果与文献[14]理论相符. 根据成功率统计式,由图7也能很直观得出上述不等关系.

图7 蒙特卡洛模拟浮点解与三类归整域的关系图

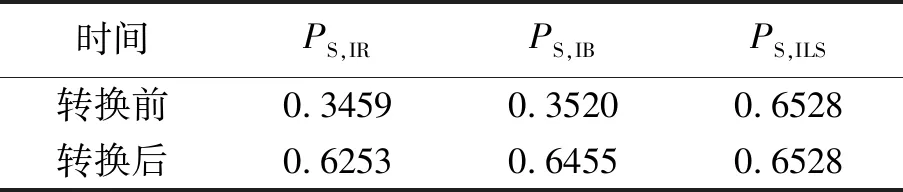
表1 三类估计方法成功率

4 总 结

针对IR、IB和ILS三类估计方法由浮点解到整数解的固定过程过于抽象,不利于对整数估计的直观理解这一问题. 本文基于MATLAB GUI设计了一套三类估计方法二维几何图形构建的可视化分析软件. 该软件可以实现三类估计方法的归整域构建、浮点解与固定解间的映射图构建、不同精度下浮点解的蒙特卡洛模拟以及成功率计算等功能. 实验测试数据表明该软件性能稳定,可以满足对三类整数估计方法几何图形表达的需求,并有助于直观形象地理解整数转换对模糊度估计的影响,也对模糊度估计方法的教学演示具有很好的辅助作用.