双边市场视角下企业创新与非价格竞争

白 崭 副教授

（1、云南财经大学 云南昆明 650221；2、武汉商贸职业学院 湖北武汉 430205）

传统的单边市场研究的是边际成本定价理论，而在双边市场中对平台上交易量起决定作用的不再是价格总水平而是价格结构，因此双边市场的中平台企业的定价策略天然存在非对称性。本文分别比较了限定创新次数条件和无限创新次数条件下卖端用户的创新竞争模型，在限定创新次数条件中，本文的研究结果表明平台企业的最优定价策略分两步走：对卖端用户的最优定价决策可以充分挖掘卖端用户的创新能力和生产剩余，对买端用户的最优定价决策不仅可以最大程度地吸引买端用户加入到平台当中而且可以有效抑制卖端用户之间激烈的价格竞争。

双边市场模型设置

（一）基本的模型

在实验中，设在双边市场中平台对双边收费标准为此：f为平台企业收取卖端的费用，Pb为买端所提交的平台费用，其中假设平台企业的收益为平台在双边获取的平台费用。图1 可以细致化的表达平台和双边企业之间的关系。

笔者采用逆向归纳法进行分析，假设已知Pb和f，可分析平台市场的均衡条件是什么。在此基础上，再假设在有限的条件下，设定卖端用户的创新条件，笔者就可以找到平台企业可以设定的最优价格。最后笔者将动态要素加入卖端用户的创新中并进行量化分析。

图1 双边市场概况

（二）平台企业

由于市场的产品质量并不相同，采用k=1，…，n代表各个产品质量情况，产品质量随k值得增加而增大。笔者采用z变量表示各个买端的购买意愿，服从正态分布的：z～U[z_,z_]。遵照前人的研究方法，收集了具有n种产品的质量数据，设定两个产品市场从而求出市场的均衡条件。

考虑到买端平台费Pb的情况下，设买端用户的效用函数如下：

式（1）中，uk为质量为k的产品的使用价值，并且u0＜u1＜…＜un也就是产品质量越高，则价格越高。只有买端用户有购买行为时，平台费Pb才需要支付。此时用户也需要支付。zk为无差异水平，也就是买端用户购买意愿的不同程度，对于质量为k的产品和k-1 的产品在各自相对价格水平下，zk依旧是无差异的。由此得到：

由式（1）得，当买端用户的购买意愿大于zk时，对收取平台费pk的质量为k的产品的偏好大于收取平台费pk-1 的质量为k-1 的产品的偏好。观望的买端用户不采用平台购买或者用其他方式购买时，它不需要支付Pb，即U(z,0,Pb)=u0z=0。

从式（2）推出下列无差异水平：

沿用Shaked 和Sutton 的方法，这种假设的方法对于均衡特征的求证提供了一种较为简便的方式。其他条件情况下，当出现三家或者更多的企业进行市场服务时，会使得均衡特征的求证过程更加复杂。

两种产品品质的市场均衡

承接上文的假设1，本文将买断用户的平台费用Pb加入考虑，利用式（3）和（4），得到:

式（5）和（6）分别是通过对z1和z2进行分析，进而对买断用户在高低端产品的企业进行选择的意愿是否存在差异性进行分析，具体如表1 所示。

将连着的一阶条件进行相交之后的交点就是均衡利益点。在这个均衡利益点上，可以得到，这两类的企业是对整个市场进行共享的。其中，这两类产品的无差异水平是要超过下界z_的，否则就会存在高品质现有企业会对整个市场获得的情况。

从图2 中可以看到，区间Ⅰ的下界z2=z_且z1=Pb/u1，上文中提到的均衡点是存在的，这样就一定会存在高品质企业的一阶条件是满足z2≥z_的。这主要是因为在竞争对手的产品价格不变的前提之下，不管是高品质企业，还是低品质企业，其收入函数都是凹函数，所以二阶条件自然满足。考虑到z_＞2z_，在图2 中，高品质公司的一阶条件满足：在z1=Pb/u1这一点上要高于z_。重新整理得到：

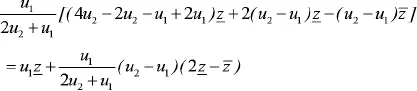
由此，可以发现，鉴于2u2+u1＞3u1，可以得到[u1/(2u2+u1)]＜1/3。结合2z_-z_＜0，由此可以证明下界小于上界。三个均衡的区间都是可行的，价格以及收入都是呈现正向的。

在区间Ⅰ中，平台对于买端用户收取少部分的费用将会吸引更多的买端用户，当平台费用收取较低，甚至是免费时，那么前文所提及到的第二类买端用户也会参与到平台之中。当价格足够低时，不重视质量的群体会直接越过平台来进行低品质产品的购买，那些重视产品质量的群体不会成为平台的潜在用户。在区间Ⅱ中，买端用户的平台费高于一定的门槛值，与区间I 相比较可以得出，买端用户主要面临的是一个相对较高的平台进入壁垒，所以一定程度上可以对现有企业的竞争程度进行一定的中和。在均衡的条件下，低品质的企业一定程度上会将价格设定在某一无差异水平上。随着买端用户平台费进一步提高到区间Ⅲ，竞争中的现有企业会根据购买者意愿较低的用户进行剔除。所以，这一部分市场没有被覆盖到。

笔者对市场上低品质的水平u1和质量差异水平u2-u1之间的关系，进行函数构图。可以发现的是：质量差异水平很低，但低品质水平较大时，均衡点将会落在区间Ⅰ内。在这种情况下，平台会有很强的需求以及购买的意愿，卖端的产品差异化程度较低，企业之间的竞争是比较激烈的。然而，当低品质水平较低时，低品质的产品对于买方而言具有较低的效用，所以会限制买方的购买意愿，因此均衡点落在了区间Ⅱ内。随着低品质水平越来越低，均衡点由区间Ⅱ转移到区间Ⅲ中，在这个过程中会出现现有企业之间的价格竞争程度的逐渐减缓。当出现产品的差异化程度较大时，如果低品质水平较高，均衡点落在区间Ⅱ内，这种情况下，企业价格的竞争在一定程度上会得到中和；如果出现低品质水平较低的情况，那么买端的用户的购买意愿也会受到影响，购买意愿的用户将会退出平台，因而会出现空白的市场。

为了进一步对现有企业的均衡定价和收入与买端用户的平台费之间的关系进行证明，在区间Ⅱ中，∂R*1/∂Pb是关于Pb的减函数，可得：

综上，当Pb满足Pb≥1/3[(2u2+u1)_z-(u2-u1)z]，区间Ⅱ和区间Ⅲ中现有的企业均衡价格和收入与买端用户平台费之间是呈现负相关关系。这表明了如果平台进行买端用户费用的提升，那么现有的企业就会对现有的买端用户进行一定的补贴。在均衡的条件下，买端用户的平台费用越高，由于企业的补贴将会造成企业成本的增加，进而导致企业收益的减少。基于价格的角度，有如下两点：

表1 均衡条件下区间I、II、III 的边界条件

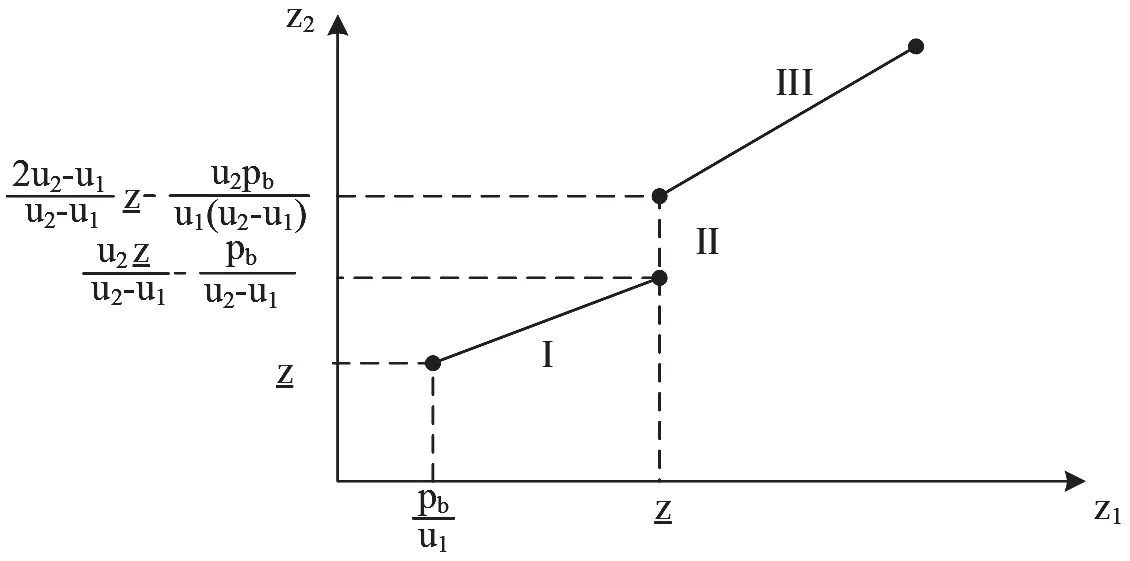
图2 低品质现有企业一阶条件

首先，买端用户的平台费并不会对买端用户的规模造成影响，而有可能只是对卖端均衡收入产生了一个消极的交叉网络外部性。例如，在区间Ⅱ中，现有的企业对买端的用户进行补贴，所以买端用户将会参与到平台之中，并且成为买端一侧，在这个区间内，平台费用的提高并不会导致买端用户需求量的减少。

其次，当买端平台费较低时，上述消极的网络外部性的影响是可以忽略的。前文在区间Ⅰ的均衡中提到的，现有企业在区间Ⅰ会通过对平台费用进行激烈的价格竞争，力求更大的市场份额。所以，现有企业的均衡收入在该区间中是与平台的费用相独立的，市场不存在空白，完全被覆盖。所以，平台的费用可以提高，在此同时，需求量也不会流失。由此可以看出，平台企业的最优定价至少是大于等于这一水平的。

在区间Ⅲ内，尽管企业在竞争情况下仍然要进行买端用户的补贴，但是买端用户费用如果不断地增加，这种补贴的方式始终不能将所有的买端用户进行挽留，所以区间III 中买端用户平台费的增加会导致买端用户的规模和现有企业的收入的减少。

双边市场下企业创新和定价策略

在有限时域中，企业在选择创新时会面临一个两个阶段的问题。在这种假定之下，笔者分析并且得出平台最优的买端平台费和卖端平台费。在无限时域的情况下，笔者将动态的特征并入到创新竞赛中，同时引入了企业的创新。通过量化的结果进行平台企业对双边收取的平台费对企业均衡条件下创新率的影响来进行求证。首先对概念的解释为：

假设市场上共有M 个同质化企业同时进行研发和创新竞赛。用εc(φi) 表示企业i 的可变的研发成本，其中ε 是作为常数参数。根据Segal 和Whinston 的假设，可以假定上述企业的成本函数是凸函数，并且表示为c(φi)=φi2，由此可得企业的创新成本是不断提高的。用φ ∈[0,1] 来表示企业i 的创新率及完成一个成功的创新研发的概率。

所有企业是同质的，所以假设这是一个对称均衡模式，也就是说所有的企业都是有相同的创新率。用π（φ）表示当M 家企业的创新率服从φ ∈[0，1] 时至少会有一家企业进行研发成果的得出的概率，成功的创新成果进入市场的概率rM(φ) 表述为：

（一）限定创新次数条件

在两阶段模型中，不管哪家卖端企业都需要在每一个阶段做出自己的决策。不进入市场的企业收入为0，企业如果要进行创新，都需要承担卖端平台费。

如果现有企业的均衡收入越高，平台企业就会适当的时机进行买端用户补贴，在一定程度上汲取卖端用户的剩余价值，从而吸引更多的买端用户。此外，买端用户的消费倾向如果不够集中，那么企业也就不会对购买意愿较低的买端用户进行关心，所以也需要平台企业进行买端用户的平台费用的补贴来进行收入的增加。同理可得，买端用户如果对于不同品质的产品表现不出购买意愿的变化，那么企业的竞争就会更加激烈，一定程度上会导致市场价格的降低，市场在企业的刺激之下会变得更加活跃。

产品品质差异化程度某种程度上会对最优化配置平台两端的平台费起到决定的作用。产品品质差异越大，那么现有企业之间的竞争就会呈现更加平和的状态，进而会对企业的均衡收入起到提升的作用。

（二）无限创新次数条件

越高的市场进入可能性越会降低现有企业的期望价值，因为现有企业会因为新进入者的创新而滑落为低品质企业甚至退出市场。

本文研究的是一个卖端企业之间的马尔科夫均态平衡问题，均衡价格存在跨期独立。

定 义 算 符T : B(X) →B(X) ，，则贝尔曼方程式（A1）可以表式为ν=Tν。至此，可以得出最优价值函数v是T的映射中的一个固定点。本文继而检验了Stokey 和Lucas 提出的理论2 的要求即布莱克维尔收缩的充分条件。

其中，V A(φ) 表示当其他卖端用户的创新率为φ 时，一家是始终参与创新竞争的企业的价值函数。当φ`=φ时，所有的卖端企业采用相同的创新率。如果V A(φ) ≥0，则最优创新率φ`=φ；否则，没有企业会参与创新竞争。创新率是由下列等式决定的：

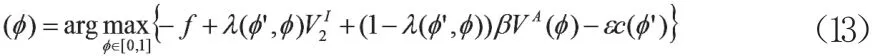
假定Pb是给定的，变动卖端用户平台费f。当卖端用户平台费f超过企业的期望创新回报值时，没有企业会参与到创新竞赛中。因此，笔者的研究重点放在对称均衡模型即所有的企业都参与创新活动，从而研究卖端用户平台费对均衡创新率的影响。

不难发现随着卖端用户平台费的增加，企业均衡创新率也随之提高，其经济学原因在于卖端用户平台费的增加变向增加了企业创新成本，从而刺激企业在创新和研发上投入更多的精力以期望获得一个较高的创新成功率和市场领先机会。因此，随着f 的增加，企业创新的失败成本越来越高，期望创新回报值则有所减少。简单来说，f 的提高加剧了企业的危机意识，变向刺激了企业的创新积极性，从而提高了企业的创新率。

结论

在限定创新次数条件中，笔者的研究成果表明一方面平台企业尽可能地提高卖端用户的平台费来获取更多的卖端企业剩余价值，另一方面对于买端用户，平台企业要根据买端用户对不同品质产品购买意愿的差异化程度高低来决定是否收取买端用户平台费、收取多少以及是否补贴。对于平台企业而言，最优的双边定价策略一方面可以尽最大可能地吸引、刺激平台上买端和卖端用户参与到平台当中，另一方面最优的买端平台费定价策略可以在一定程度上中和卖端用户的价格竞争，减少卖端用户为盲目占有市场份额而经济无效率地自发补贴买端用户。在无限创新次数条件中，当所有的卖端用户都参与到创新竞争中，参数结果表明不断增加的买端用户平台费会变向抑制企业的创新积极性，反而较高的卖端用户平台费会刺激均衡状态下整个市场的整体创新率。

总之，在平台企业的市场中，竞争关系的企业是纵向上具有差异的且是根据买端用户的爱好来设定价格的。在同一市场上，具有高品质的产品企业是有可能被其竞争者的创新产品超越的，导致高品质企业变为低品质企业。