“数”山有路“形”为径

林振伟

著名数学家华罗庚曾说过：“数形本是相倚依，焉能分作两边飞，数缺形时少直观，形少数时难入微，数形结合百般好，隔裂分家万事休。”在数学教学中，无论是教师还是学生都需要用到数形结合的思想方法，让复杂难懂的数量关系变得简单、明了、形象，使我们的数学学习事半功倍，下面我浅谈一下在数学教学中我对“数形结合”的应用。

一、 数形结合，能激发学生学习兴趣

无论我们做什么，兴趣无疑是最好的老师，有了兴趣，做什么都有了精气神，有了动力，小学生学习数学亦是如此。

对于小学生来说，他们的大脑发育还不完善，对于一些抽象的概念知识，他们还不能够很好的去理解，因此这就需要老师将那些抽象难理解的知识转换成具体的形象的事物来帮助他们理解。学习有余数的除法知识时，有道题是这样设计的：六一儿童节快到了，我们要去布置会场，先搬来23盆花，每组摆5盆，可以摆几组，还剩几盆？对于初学除法的孩子们来说，他们还像丈二的和尚摸不着头脑，这时老师开始提示这些小家伙们了，你可以用圆圈当做一盆盆的花，在练习本上先动手画一下，大家试试看。这时，爱动爱画的小朋友们立刻兴致勃勃的圈画了起来。就在简单的画的过程中，他们对有余数的除法有了一个最基础的认识，对这类题目的第一个感觉就是有趣。如果数学课堂上教师能让每位学生都感到“有趣”，积极的参与到课堂中去，那么精彩纷呈的课堂绝不在话下。

二、 数形结合，让学生由“模糊”变“清晰”

小学阶段的学生们还处于形象思维阶段，难以很好的理解比较抽象的知识，帮助他们最好的方法就是把抽象的数量关系用简单的图形加以表示，这样就使得学生对问题的认识由“模糊”变“清晰”，这就是数形结合的精髓。

在解决问题中我们经常会遇到这种类型的题目：妈妈给小明买了一个书包和一个文具盒，文具盒的价钱是13元，书包的价格是文具盒的3倍，问妈妈买书包和文具盒一共花了多少钱？书包比文具盒多花多少钱？

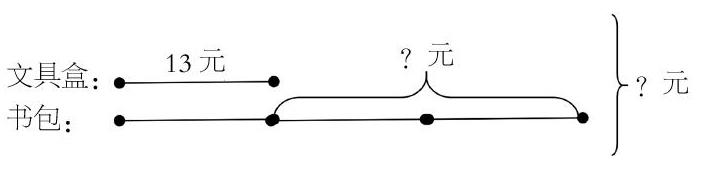
此时学生的大脑是处于混沌状态的，因为他们并不知道一个书包多少钱，要求计算出妈妈买书包和文具盒一共用了多少钱？这时用倍比的知识来解决此问题是比较抽象的，但是线段图却起到了良好的作用，如下图所示：

通过线段图可以看出书包是3个文具盒的价钱，也就是：

13×3=39（元），总价钱就是39+13=52（元）书包比文具盒多花的钱就是39-13=26（元）。

就这样，模糊的数量关系借助一个简单的线段图，变得清晰起来，从而很好的理解了倍比关系的做法，学习的信心也增强了！

三、 数形结合，能够突出重点，突破难点

在日常教学中，我们都会这样告诉我们的，无论解答什么样的题目，都要先找到这个问题的核心——问题的重点、难点，学生如若能顺利的找到问题的重点，解决问题也就顺理成章。但小学生的抽象思维能力、空间想象能力都还有所欠缺，有时他们仅凭空想象考虑问题往往会不周密、不严谨，进而影响解题的正确率。这时，老师如若能引导学生利用数形结合的思想来画一画，以画促思，则能对学生起到更好的帮助作用。

例如：学习了新人教版五年级数学下册“长方体和正方体的表面积”这部分知识后有这样的一道习题：把2块棱长为1.5分米的正方体木块拼成一个长方体，这个长方体的表面积是多少？不出所料，有些同学很快算出27平方分米，还有些同学认为不对，但又说不出问题所在。看到学生的窘境，我轻轻提醒一句：我们已学过画长方体和正方体了，你为什么不拿起笔来画图看看呢？这时同学们茅塞顿开，纷纷动笔，热闹的课堂一下子安静下来，不一会，听见下面有同学在喊：“不是27平方分米，而是22.5平方分米！”……响应的同学越来越多，有的同学迫不及待的举着画好的图，是22.5平方分米！是22.5平方分米！刚才的疑问也在大家动手画画的过程中解决了。根据学生们画好的图，我又开始刁难他们了，同学们仔细看看，有几种方法可以解决这个问题呢？不一会，已经发现问题重点的他们就想到了所有的方法：

方法1：两个正方体拼成了一个长为3分米，宽为1.5分米，高为1.5分米的长方体，根据长方体的表面积公式，该图形的表面积为：

（3×1.5+3×1.5+1.5×1.5）×2

=11.25×2

=22.5（平方分米）

方法2：两个正方体拼成长方体后有2个正方形面消失了，所以长方体的表面积为：

1.5×1.5×6×2-1.5×1.5×2

=27-4.5

=22.5（平方分米）

这种由一些图形组成的新图形的表面积，并不能直接把两个图形的表面积直接加起来，问题的重点难点在于这些图形拼成新的图形后原来的一些面可能不再是新图形的面了，而变成了新图形的内部，由表面积的定义即可知这些成为内部的面在计算新图形表面积时是不能算进去的，这样把问题的重点突出，难点突破，问题就迎刃而解了。

四、 让学生形成用数形结合解决问题的习惯

小学数学中的很多知识都可以借助数形结合的思想方法来解决，如：认识整数、分数、减、乘、除解决问题，倍的问题、图形组合问题等等，其中复杂的数量关系都可以借助简单的图形变得简单明了，也就是“数”山有路“形”为径。

“数”山有路“形”為径，我们在平时的数学教学中要多加渗透学生对各种数学思想方法的学习，数形结合尤为常用，学生养成用数学的思想方法解题后，数学思维能力、解决问题的能力也会随之提高。