分类思想在中学数学的应用与教学

杨振中

摘要：分类思想是中学数学中常用的一种数学思想，在中学数学解题中的应用非常广泛。它是利用题目所给的参数进行分类，把复杂的问题分为若干个比较容易的问题来解决。在分类思想的教学方面应该尽量体现分类思想的应用，让学生在运用分类思想的实践中加深对分类思想的理解，提高学生的解题能力和思维能力。

关键词：分类；解题；教学

中图分类号：G633.6文献标识码：A文章编号：1992-7711（2020）07-0162

分类思想是用在中学数学解题中一种常用而且很重要的思想，它在其他学科也占有很重要的地位。其中在中学物理学和化学等其他自然学科中的应用也非常频繁。

一、分类思想的定义和它在数学方面的表达形式

分类就是按照事物间性质的异同，将相同性质的对象归于一类，不同性质的对象归于不同类别的思维方法，它是一种逻辑方法，同时也是一种数学思想。分类的思想就是当我们面临的数学问题不能以统一形式解决时，可以把已知条件的范围划分若干个子集，在各个子集内分别讨论问题的解。然后通过综合各种解而得到原问题的解答。用数学式子来表达时我们可设符合这一问题所有的元素组成一个集合P，依据元素某些性质可将集合P无遗漏、无重复地分成若干个真子集P1、P2、…、Pn，（即满足：1. P=P1∪P2∪…∪Pn。2. Pi∩Pj=？，i，j∈{1，2，…，n}则称P1、P2、…、Pn是集合P的分类。）如有必要还可以对Pi再进行分类，构成二级分类，依次类推。

二、分类思想在中学数学解题中的应用

在中学数学中，分类思想运用是相当广泛的。在笔者多年的教学中，笔者感受到几乎是每一章节的内容都有运用到分类思想。这不仅体现在日常教学中，而且体现在解决问题的过程中。如果在解题的过程中，你对某一适用于分类思想的题目采用了分类讨论的方法后，你会发现它比原来的方法快捷了许多。下面，我们结合求解曲线方程、三角函数、不等式、排列组合的例子来研究分类思想在中学数学解题中的应用问题。

1.分类思想在确定曲线方程中的应用

此类问题是根据曲线的参数分类，且由曲线的定义来确定曲线的方程。在做的过程中前提是要熟知各类曲线的方程表达式，然后结合所给的参数分为若干个区间来讨论。其中在划分参数区间的过程中找到临界值是非常关键的。如：

例1.讨论方程（m-3）x2+（5-m）y2=1所表示的曲线。

分析：因为m-3，5-m的正、负是决定曲线为双曲线或椭圆（含圆）的根据，所以使m-3=0，5-m=0的值成为划分的标准；又因为m-3，5-m的相对大小又决定焦点在哪一条坐标轴上，所以使m-3=5-m的值也是划分的标准，这样抓住m=3，4，5这三个数量临界就可以进行讨论。

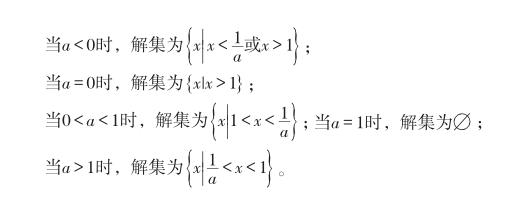
4.分類思想在排列组合中的应用

由排列和组合这章节的加法原理的定义，我们就可以知道排列和组合本身就是一个分类思想的产物。在课本上的一些解决问题的方法，笔者认为也是由分类思想得到的。在经过几年的中学学习中，学生在不断的学习中慢慢地掌握了分类思想，到了排列和组合这章节的时候就是要运用这一思想的时候。并且在这一章的时候也是他们在这一方面得到充分锻炼的时候。

例.某车间有10名工人，其中4人仅会车工，3人仅会钳工，另外三人车工钳工都会，现需选出6人完成一项工作，需要车工，钳工各3人，问有多少种选派方案？

分析：如果先考虑钳工，因有6人会钳工，故有C63种选法，但此时不清楚选出的钳工中有几个是车工钳工都会的，因此也不清楚余下的七人中有多少人会车工，因此在选车工时，就无法确定是从7人中选，还是从6人、5人或4人中选。同样，如果先考虑车工也会遇到同样的问题。因此需对全能工人进行分类。

（1）选出的6人中不含全能工人；（2）选出的6人中含有一名全能工人；（3）选出的6人中含有2名全能工人；（4）选出的6人中含有3名全能工人。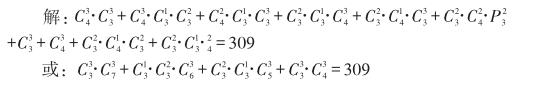

5.错用分类的情况

分类思想是一种重要的数学思想方法，是一种数学解题逻辑思维方法，使用分类思想解决问题要视具体问题而定，并无死的规定。但可以在解题时不断地总结经验，常见的“个别”情形略举以下几例。

（1）“方程ax2+bx+c=0有实数解”转化为“Δ=b2-4ac≥0”时忽略了个别情形：

三、在教学中使学生循序渐进理解和运用分类思想

学生对分类思想的理解和应用应循序渐进，由浅入深，不能也不可能一步到位。在学生了解了分类的定义后，笔者在基础知识的讲授和解题指导中充分利用教学内容，尽量体现分类思想的应用，让学生运用分类思想的实践中加深对分类思想的理解。例如，在函数最值的教学中，笔者对二次函数y=ax2+bx+c（c≠0）最值的讨论，作了这样的安排。

第一阶段，根据二次项系数a>0和a<0的两种情况讨论最大和最小值。

第二阶段，在a>0（或a<0）的前提下，在某个闭区间[]α，β内分包括端点与不包括端点两种情况来讨论。

例.已知函数y=x2-2x，根据以下不同条件求函数的最大值和最小值，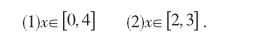

第三阶段，进一步变换为在某个不定区间上的最值讨论；或者变换为某个不定函数在指定区间上的最值讨论。

例.求函数y=x2-2ax，x∈R在[] 0，2的最大值和最小值

这样的安排使学生对二次函数的最值问题有了较清楚的理解，解决这样的问题的时候就能够得心应手了。

通过对学生的经常性训练，学生就能习惯于用严谨的思维方式处理问题，并逐步熟练利用这种方法解决相关的问题。

（作者单位：广西北海市铁山港区南康中学536017）