水文循环算法的改进

何欣芸，周朝荣,2+

(1.四川师范大学 物理与电子工程学院，四川 成都 610101；2.成都信息工程大学 气象信息与信号处理四川省高校重点实验室，四川 成都 610225)

0 引 言

近年来，受自然界中水运动的启发，一些基于水的智能优化算法迅速发展起来。Hosseini基于河流中水滴间的作用与反作用，提出智能水滴算法[1]。Yang等模拟水流运动设计出类水流算法[2]。Rabanal等借鉴河流形成动力学来解决NP-Hard问题[3]。通过观察水的循环过程以及河流、溪流的运动，Eskandar等设计出水循环算法，并应用于约束优化问题的求解[4]。Wu等受浅水波模型启发，提出水波算法[5]。这些受水运动启发的算法由于参数少、易调节、模型简单等优点受到了许多学者的关注。

然而，上述算法只涉及到自然界中水运动的部分过程，未考虑到完整的水循环运动，只模拟水运动的部分过程会限制算法搜索能力，造成算法早熟收敛。为此，Wedyan等模拟水的循环再生过程提出水文循环算法(hydrological cycle algorithm，HCA)，并通过仿真实验验证水文循环算法在连续问题与离散问题上均优于仅模拟部分水运动的算法[6,7]。其中，水文循环是指水在自然界中的连续循环运动，包括水受重力与地势影响从高处向低处流动、受阳光照射蒸发到大气层以及在空中凝结成水滴重新落回地面等阶段。HCA利用完整的水循环过程，为算法设计提供新的思路。

然而，HCA仍存在收敛速度慢、寻优精度不高以及运行时间较长等问题。为此，本文首先在HCA的种群初始化阶段采用混沌的方法，强化全局搜索能力、加快收敛速度；其次，自适应产生温度更新参数，以减少算法的运行时间；最后，在凝结阶段引入逆水流过程，以提高算法的寻优精度。为验证改进后的算法性能，在10个经典函数上进行仿真测试，并与粒子群算法[8]、遗传算法[9]与鲸鱼算法[10]进行比较。测试结果表明，改进后的算法在寻优精度、收敛速度以及运行时间上较HCA表现更优，且总体性能优于粒子群算法、遗传算法与鲸鱼算法。

1 水文循环算法

1.1 流动阶段

水滴在具有数条等高线的山形图上进行流动，山形图个数由函数的维度决定，等高线条数由算法精度决定，越靠近山顶的等高线所占权重越大。

水滴从山顶出发，在每层等高线上选择移动到某个节点。水滴遍历完所有等高线后，各个维度中存储着水滴在该维山形图的等高线上所选节点。

流动阶段涉及到节点选择与次数、速度、土壤量、温度的更新，实现原理如下：

(1)节点选择

水滴在山形图上移动时，根据下一层等高线上节点的选择概率，采用轮盘赌的方法选出节点。水滴在节点i的位置选择下一层等高线上节点j的概率给出如下

(1)

移动到新的节点后，立即更新该段路径被选次数、土壤量以及水滴的速度和所携带的土壤量。

(2)温度更新

一次流动阶段结束时，基于此时水滴的适值差异更新温度

Temp(T+1)=Temp(T)+ΔTemp

(2)

1.2 蒸发阶段

在蒸发阶段，被蒸发的水滴的个数随机生成，用轮盘赌的方法选择出被蒸发的水滴。

1.3 凝结阶段

蒸发后的水滴按如下方式进行变异

(3)

1.4 降雨阶段

在降雨阶段，若达到最大迭代次数则输出最优解；否则，重新初始化动态变量与参数，利用本次迭代得到的最优解对动态参数进行加固处理，以指导下一代寻优。参数加固计算如下

Soil(i,j)=0.9×Soil(i,j) ∀(i,j)∈BestWD

(4)

其中，BestWD表示本次迭代得到的最优解，∀(i,j)∈BestWD表示该最优解在流动阶段所选路径。

2 改进的水文循环算法

HCA的初始水滴种群随机产生，多样性难以保证，会对算法的性能造成显著影响，初始种群分布越均匀的算法具有更高的收敛速度与寻优精度[11]。为此，考虑混沌方法丰富初始种群的多样性。其次，HCA将温度更新参数设置为固定值，个别优化函数在流动阶段内循环多次，以致算法运行时间过长。因此，针对不同的优化函数设置不同的温度更新参数。最后，为解决寻优精度低的问题，基于原算法中的山形图，提出水滴逆向运动模型，即“逆水流”过程。该过程舍弃原算法流动阶段中的复杂参数与公式，不仅模型更为简单，且有效地提高了算法的寻优精度。

2.1 混沌初始化

混沌是具有遍历性、半随机性以及初始条件依赖性的一种非线性系统[12]。与随机初始化相比，利用混沌进行初始化可以产生分布更均匀的初始种群[13]。Skew Tent混沌映射模型简单、具有较好的遍历性，且初始条件的依赖性低。本文采用Skew Tent混沌映射对水滴种群进行初始化[14]

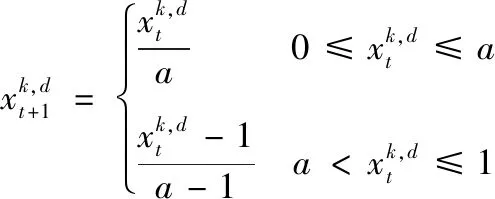
(5)

(6)

2.2 自适应温度更新参数

HCA在优化某些问题时，一次流动阶段结束后的水滴适值相差较大，温度增长缓慢，算法在流动阶段多次循环，最终导致整个算法的运行时间过长。为此，采用自适应温度更新参数代替原算法中固定的温度更新参数，由初始种群的适值来决定温度的增长速度，从而降低算法的运行时间。

在种群初始化阶段结束后，评估水滴种群的适值，根据最差适值ψmax与最优适值ψmin计算温度更新参数

(7)

2.3 逆水流

针对HCA容易陷入局部最优的问题，利用已有的山形图，设计逆水流代替原凝结阶段的变异操作，以提高算法的寻优精度。

水滴开始逆流时，首先从山脚出发，向高层等高线移动。在此过程中，同层等高线上的节点间彼此连通，水滴在同层等高线上移动后，再移向更高层的等高线。对应的逆水流过程如图1所示。

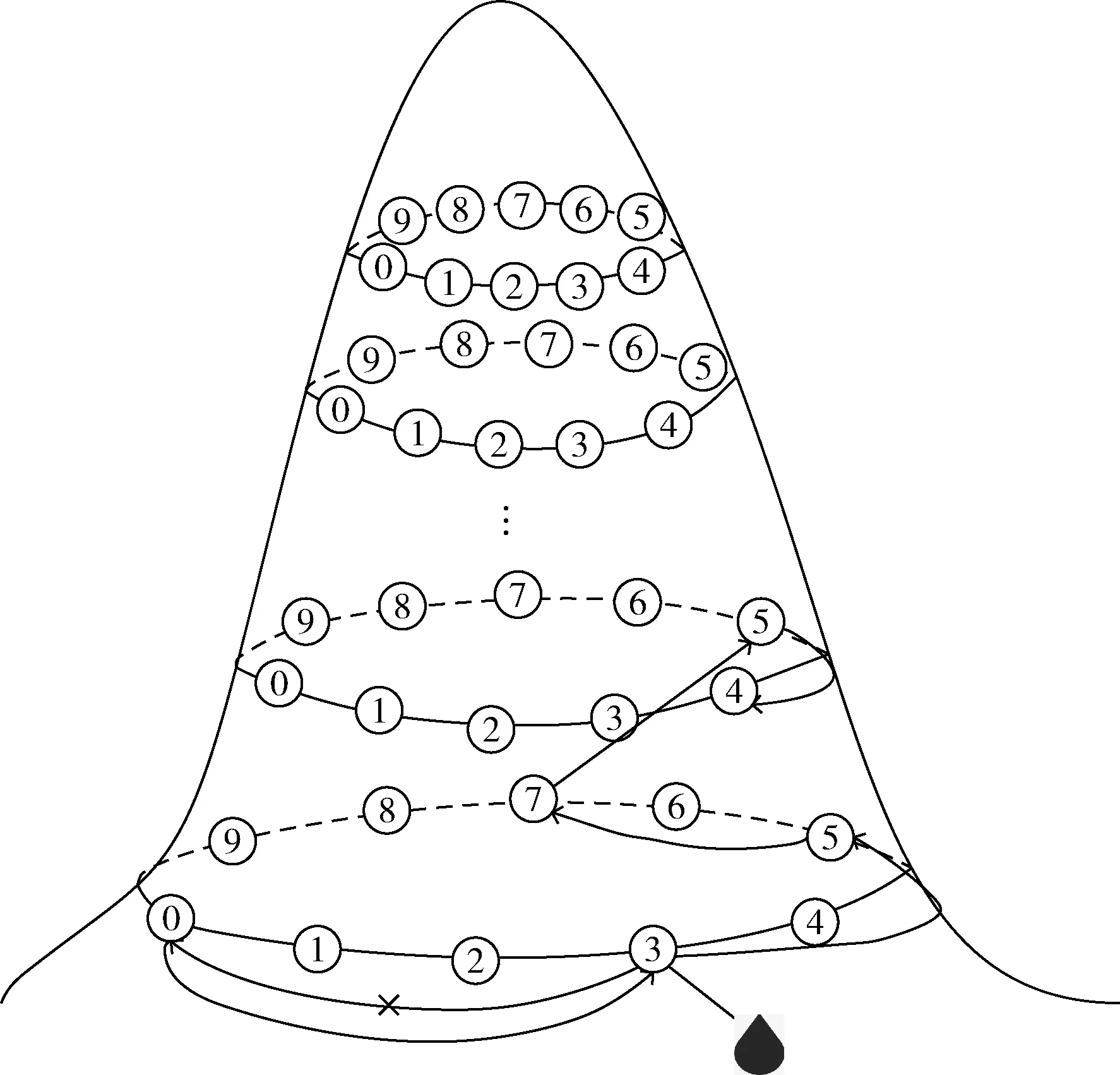
图1 逆水流过程

水滴在某一层等高线上移动时，随机选择一个节点数值比原节点数值小的节点，然后评估该节点。若对应的水滴适值优于原节点，则替换掉原节点，并继续随机选择一个数值更小的节点，直至选择数值更小的次数达到上限。

若所选节点对应的水滴适值更差，或原节点的数值已是最小，或选择数值更小的次数已达上限，则在该层随机选择一个节点数值比原节点数值更大的节点。进一步地，评估该节点，若适值更优则进行替换，并继续选择数值更大的节点直至次数达到上限；若适值更差，或是原节点的数值已是最大，则水滴流入上一层等高线。

水滴逆流的完整过程见表1。

表1 逆流过程

当流动阶段结束后，每颗水滴生成的解以节点数组的形式存储在水滴中。在逆流过程中，水滴首先改变底层等高线上的节点，由于底层等高线所占权重小，此时可视为局部搜索；当水滴逆移动到较高层等高线时，可视为全局搜索。

2.4 改进算法的流程图

HCA结合上述混沌初始化与自适应温度更新参数策略，得到温度自适应水文循环算法(THCA)；HCA结合上述混沌初始化与逆水流策略，得到逆水文循环算法(IHCA)；HCA同时结合上述混沌初始化、自适应温度更新参数以及逆水流策略，得到温度自适应逆水文循环算法(TIHCA)。其中，TIHCA的流程如图2所示。

图2 温度自适应逆水文循环算法流程

3 实验结果及分析

3.1 实验环境

仿真实验的运行环境为Intel Core i7 CPU，主频2.40 GHz，内存8 GB，Windows10 64位操作系统，实验仿真软件采用MATLAB R2016a。

3.2 测试函数与参数设置

本文选择5组多峰基准测试函数f1-f5和5组单峰基准测试函数f6-f10来验证算法性能。表2给出了测试函数的定义、搜索空间和理论最优解。

表2 测试函数

表2(续)

所有对比算法都统一设置种群大小为10，最大迭代次数为500。针对上述每个函数，每种算法均独立运行30次。对比算法与参数设置见表3、表4。

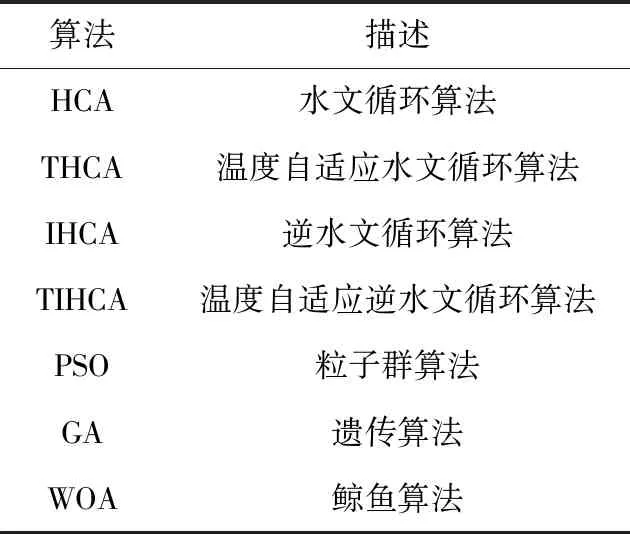
表3 对比算法

表4 各算法参数设置

3.3 算法寻优精度比较

所有测试函数的实验结果见表5、表6。

从表5可以看出，对于多峰测试函数f1-f5：在函数f1、f4中，IHCA、TIHCA与WOA得到相同的最优值；在函数f2、f3中，IHCA与TIHCA各项指标的值非常接近，且均优于其它算法；在函数f5中，IHCA的最差值、平均值、标准差均优于其它对比算法。

表5 多峰函数寻优精度对比结果

表5(续)

从表6可以看出，对于单峰测试函数f6-f10：就函数f6、f7、f10而言，IHCA与TIHCA准确找到理论最优值，且表现稳定；在函数f8中，IHCA与TIHCA得到相同的最优值，但IHCA的最差值、平均值、标准差优于TIHCA以及其它对比算法。

表6 单峰函数寻优精度对比结果

与HCA相比，THCA有3个函数的平均值更优，其余函数的平均结果相差不大；IHCA在10个函数中的寻优均值均优于HCA；TIHCA在9个函数中具有更好的平均值。总体而言，IHCA在寻优精度方面表现最好，而 TIHCA 仅次于IHCA。这表明逆水流策略在寻优精度上具有明显优势，而自适应温度更新参数策略虽未能有效地改善HCA的寻优精度，但减少流动阶段的循环次数未对算法的寻优精度造成不利影响。

3.4 算法收敛速度比较

各个算法针对不同函数的收敛曲线如图3-图12所示。

图3 函数f1的收敛曲线

图4 函数f2的收敛曲线

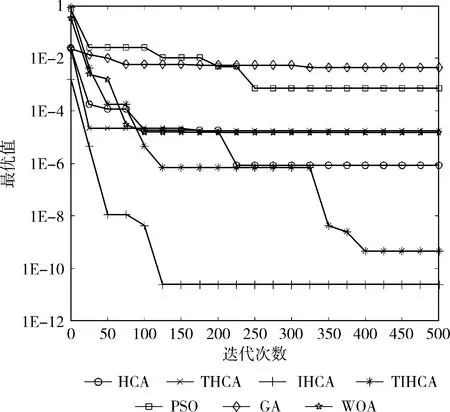
图5 函数f3的收敛曲线

图6 函数f4的收敛曲线

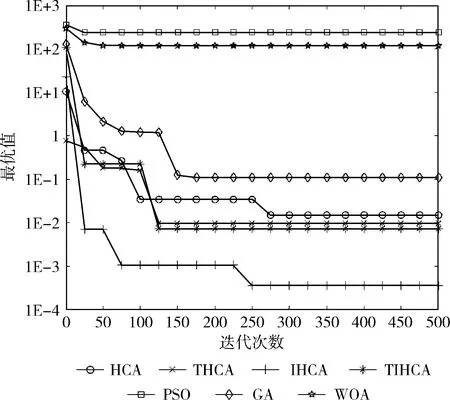
图7 函数f5的收敛曲线

图8 函数f6的收敛曲线

图9 函数f7的收敛曲线

图10 函数f8的收敛曲线

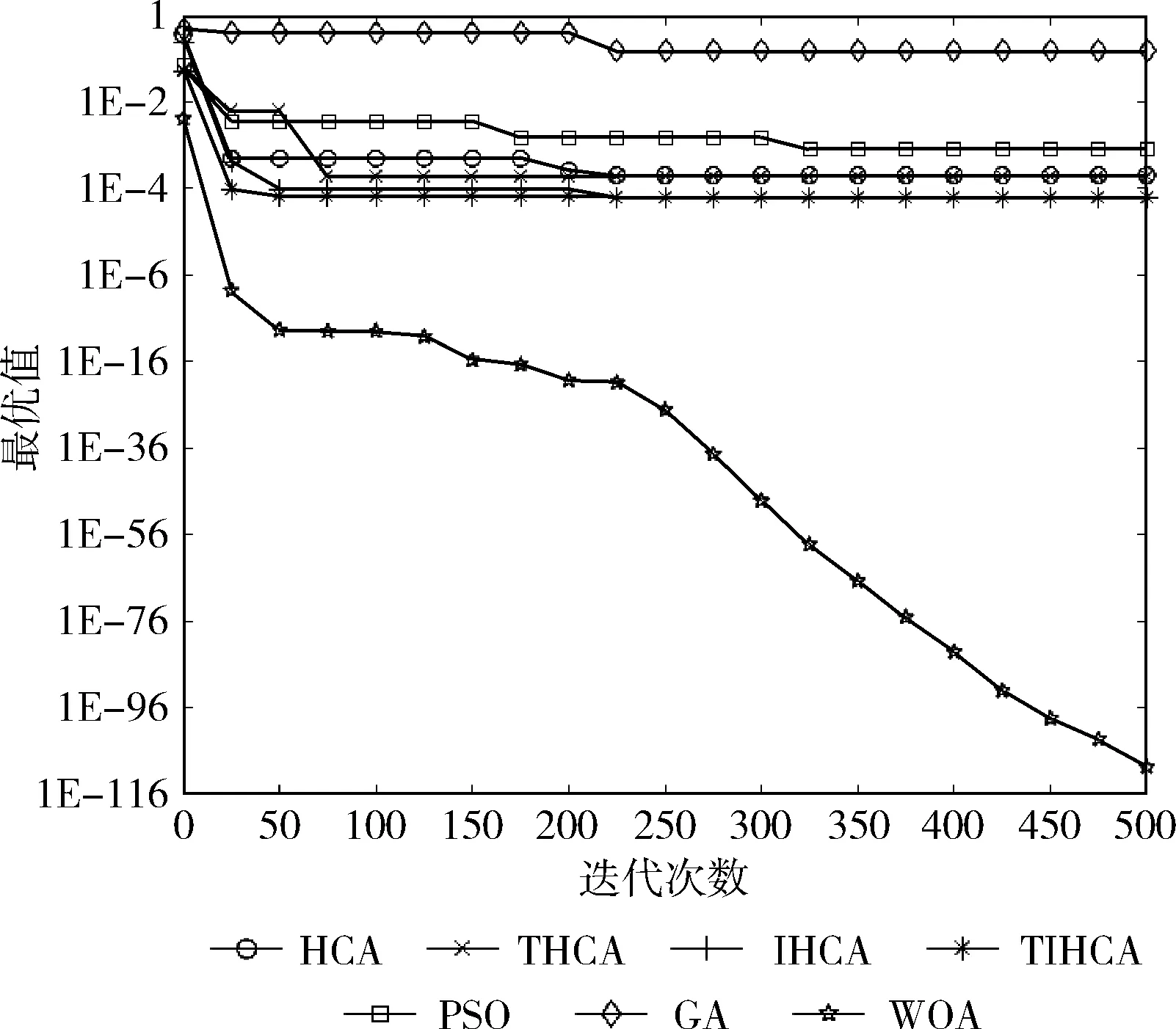
图11 函数f9的收敛曲线

图12 函数f10的收敛曲线

从图中可以看出，在绝大多数时候，所有改进的HCA都比HCA更快收敛。在函数f1-f3、f6中，THCA的收敛速度最快。虽然在函数f1、f2、f6中，PSO与THCA具有相同的收敛速度，但PSO的寻优精度较差。在函数f7、f8、f10中，IHCA具有最快的收敛速度。虽然在函数f8中，GA与IHCA的收敛速度相同，但GA的寻优精度远低于IHCA。在函数f9中，TIHCA的收敛速度最快。

与HCA相比，THCA在函数f1-f3、f5-f7、f9中具有更快的收敛速度，IHCA在函数f1、f3、f5-f8、f10中的收敛速度更快，TIHCA在函数f1、f2、f5、f6、f9中收敛更快。总体而言，THCA与IHCA的收敛速度最快。这表明各个策略对算法的收敛速度均有不同程度的提升，而混沌初始化与自适应温度更新参数的结合，以及混沌初始化与逆水流的结合在收敛速度上均有更好的改进效果。

3.5 算法运行时间比较

对算法运行30次的时间取平均值，所有对比算法的运行时间如图13所示。

图13 f1-f10运行时间对比结果

从图13可以看出，针对10个测试函数，PSO、GA与WOA的运行时间均为最短，这是由于HCA本身具有较多且复杂的参数与公式，即使改进后的算法THCA、IHCA、TIHCA运行时间仍较PSO、GA与WOA更长。

与HCA相比，THCA在函数f1-f5、f7-f10上的运行时间更短，IHCA在函数f3-f5、f9上花费更少的时间，TIHCA在函数f3-f5、f7-f10上的运行时间更短。总体而言，THCA的运行时间最短，这体现了自适应温度更新参数策略在运行时间上的优越性。而TIHCA仅次于THCA，这是由于逆水流过程的引入会增加一定的计算量。

综合上述实验结果可以看出：THCA的运行时间最短、收敛速度最快，IHCA具有最好的寻优精度与收敛速度，而TIHCA折中了寻优精度与运行时间两方面的性能指标，算法性能介于THCA与IHCA之间。在求解实际优化问题时，可以根据实际需要选择合适的策略。

4 结束语

针对水文循环算法的不足，本文采用混沌的方法初始化水滴种群，增强算法的全局搜索能力、提升算法的收敛速度；引入自适应温度更新参数策略，减少算法的运行时间；提出逆水流过程代替原凝结阶段中的变异操作，以提高算法的寻优精度。实验结果表明，改进的算法在收敛速度、寻优精度与运行时间等方面均有较大的性能提升。然而，水文循环算法自身也存在局限性：算法中包含大量参数与动态变量，以致水文循环算法以及本文中的改进算法在运行时间方面依然不如粒子群算法、遗传算法与鲸鱼算法，且求解高维函数较为困难。如何改进这些缺点，将是下一步的研究工作。