油田注水管网布局优化混合整数非线性规划模型*

张昕 周星远 张浩然 梁博文 梁永图

1中国石油大学（北京）城市油气输配技术北京重点实验室

2东京大学

3长江大学石油工程学院

油田注水系统是油田地面工程的重要组成部分[1]。油田注水系统由注水站、配水间、注水井和连接它们的管道构成，是一个复杂且庞大的水力系统。水经泵站加压后注入注水管网，经由各配水间分配到各注水井，最后经井筒注入地下以实现保持油层压力，确保油田稳产的目的[2]。整个注水系统的投资费用主要包括基础建设费用和运行费用，其中基础建设费用主要包括干、支线管线费用和注水站、配水间、注水井的建设费用。大部分油田已进入高含水开发期，每天的注水量巨大，注水生产投资较高，降低注水能耗具有必要性。现场生产习惯将大部分精力集中在注水管网运行优化方面，对注水管网拓扑布局优化关注较少，管网一旦建成，在短期内将不会有较大改动，因此在建设初期设计出科学合理的布局方案至关重要。注水管网布局设计是保证注水系统高效运行、合理开发油气资源的关键环节[3]。注水管网布局的合理性会直接影响整个系统的投资，同时布局设计结果也会对管网运行情况产生相应影响，因此对注水管网的合理布局不仅可以降低注水系统的投资成本，又可以进一步为降低注水能耗、提高生产效率奠定基础。

针对注水管网布局优化方法的相关研究，目前最主要的是分级优化法。尉亚民等[4]通过建立井组最优划分模型、配水间最优布局模型、注水站站址优化模型进行了油田注水管网的布局优化。王美薇[5]将注水管网简化为点线组合，首先进行注水井的隶属关系划分，然后以管线长度最小的原则确定配水间及注水站的位置并确定管网的拓扑结构。分级优化方法较少地考虑上级优化结果对下级优化的影响，因此根据各级优化结果得到的最终解很难保证是全局最优解。此外，也有学者通过建立整个管网的数学模型求解该问题。刘扬等[6]在油气集输管网中以管道总长度最小为目标，采用混合遗传算法求解，类似方法也可应用于注水管网布局优化中。齐晗兵等[7]将注水站、配水间、注水井简化为平面中的点，建立了树状注水管网的布局优化模型，并引入类电磁机制算法进行求解。武晓勇[8]采用改进蚁群算法确定注水井与配水间、配水间与注水站的连接关系。任伟建等[9]以注水管道总长度最小为优化目标，采用改进粒子群优化算法进行求解。以上研究均证实了优化算法求解的便利性及结果的可行性，但大多以管道总长度作为衡量投资的指标，较少考虑管径对管道建设投资的影响。

本文在基于普遍应用的单干管多井配水工艺[1]的基础上，首先运用模拟退火遗传算法划分注水井区域并确定配水间的最优位置，然后以加权距离最短为目标，运用Dijkstra 算法确定最终的注水管网拓扑结构。

1 油田注水管网

油田注水管网常见的网络形态主要分为三种：星形管网、树状管网和环状管网[10]，如图1 所示。在星状管网中节点与其所管辖的下属节点间呈星状连接；环形注水管网即配水间与注水站以及各配水间连接成环形，注水井分别连接到环形管网上[1]；树状注水管网即所有注水井与配水间呈星状连接，各配水间与注水站间以树枝状连接，即配水间之间可以相互连接。

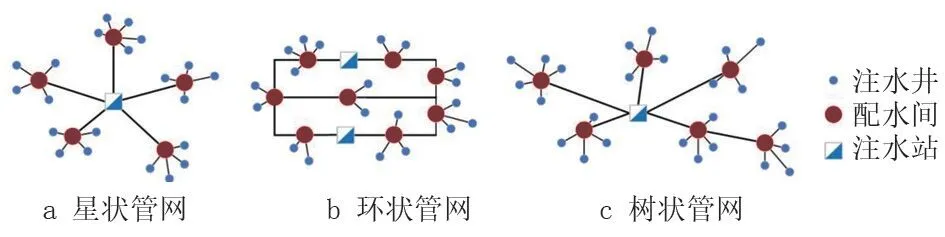
图1 三种注水管网网络形态Fig.1 Configuration of three types of water injection pipeline networks

以上三种是油田注水管网的主要形态，对比以上三种管网形态，环状管网相比其他两种管网具有造价较高的特点。树状管网较星状管网更为灵活，相比环状管网具有注水量易于控制等特点[11]。在实际生产中也存在其他形态的管网，可根据实际情况对管网的拓扑结构做出相应调整。

2 注水井组划分及配水间站址优化

2.1 数学模型

2.1.1 目标函数

先前的研究大多以距离总和最短近似代替管网建造费用最低的目标，较少考虑管径对于管网造价的影响。因考虑到注水井产量不同会导致上级配水间的处理量以及连接它们之间的管径不同，注水井的位置不同也会导致配水间的位置以及连接管道的管长发生变化，均会对注水井的分组效果产生影响，本文引入“加权距离”作为目标函数。根据经济流速法[12]初算管径，在各支线流速相差不大的情况下管径D2与流量qh近似成正比关系，又因管道单位长度造价与管径尺寸呈线性相关，因此可认为管道单位长度造价与成正相关关系[13]。在注水管网初步布局优化中，可将“加权距离”近似作为管网建设投资的衡量指标。结合以上考虑的因素，将流量作为权重建立注水井组划分与配水间站址优化数学模型［式（1）］，目标函数为各配水间到其所管辖注水井的加权距离之和最小。

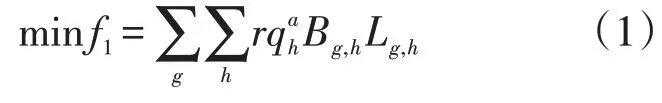
式中：qh为第h个注水井的产量；Lg,h为第g个配水间与第h个注水井之间的距离；Bg,h为判断第g个配水间与第h个注水井之间连接状态的二元变量，若第h个注水井属于第g个配水间，则Bg,h=1，否则Bg,h=0，不计入加权距离计算范围之内；γ和α分别为加权系数和指数，一般γ=1，α=0.5[13]。

2.1.2 约束条件

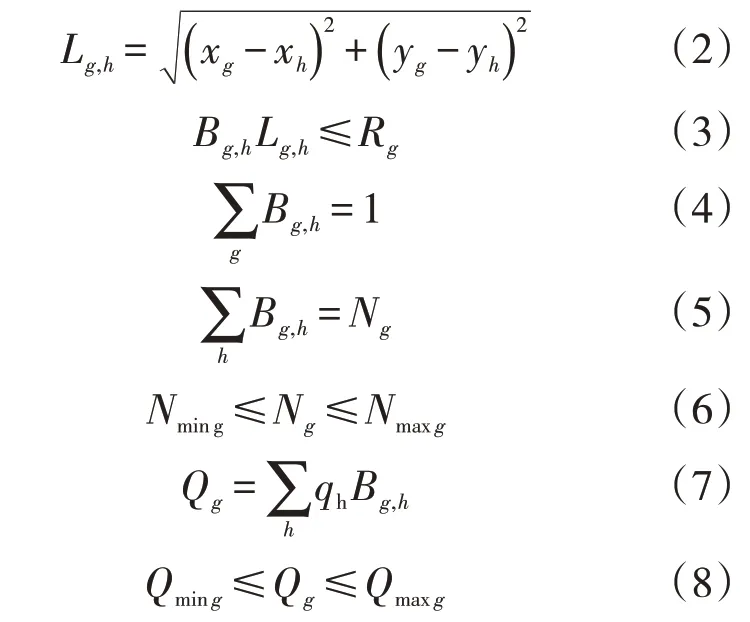
式（2）表示第g个配水间与第h个注水井之间的距离，其中(xh，yh) 为注水井h的坐标，(xg，yg)为配水间g的坐标；式（3）为配水间管辖范围的约束，其中Rg为配水间配注范围限制；式（4）为注水井隶属关系的唯一性约束，即每个注水井只能归一个配水间管辖；式（5）、（6）表示配水间管辖注水井的数量约束（一般为3～8 口）；式（7）中Qg为第g个配水间配注流量，该式表示配水间流量为其所管辖注水井流量之和；式（8）表示配水间配注流量需满足一定的范围需求，其中Qmaxg为配注流量上限，Qming为配注流量下限。

2.2 模型求解

由于本文所建立的注水井组划分与配水间站址优化模型为混合整数非线性规划模型（MINLP），采用常规的数学规划算法难以在常规时间内求得有效解，并且所建立的模型中实际包括两个子问题，分别为注水井组划分与配水间站址优化，两个问题互相耦合，即划分注水井组需已知配水间位置，而确定配水间最优位置又需已知其所需要管辖的注水井。本文选择耦合模拟退火算法（Simulated Annealing，SA） 与遗传算法（Genetic Algorithm，GA）的模拟退火遗传算法（Simulated Annealing Genetic Algorithm，SAGA）[14]对所建立的模型进行两阶段求解。模拟退火遗传算法利用遗传算法较强的全局搜索能力以及模拟退火算法较强的局部搜索能力对模型进行求解[15]。父代完成选择、交叉、变异等遗传操作后产生子代，采用模拟退火算法对子代中配水间位置进行局部搜索，产生最终子代后再次按照遗传算法的流程进入下一代。

第一阶段由遗传算法负责求解注水站与配水间的隶属关系，因为作为求解离散变量组合优化的经典算法，采用遗传算法划分注水井组具有良好的匹配性与适用性；第二阶段在配水间与注水井隶属关系已知的条件下由模拟退火算法负责对配水间位置进行优化，因模拟退火算法具有良好的局部搜索能力，在初始较优解（所管辖注水井的加权中心位置）已知的情况下能较快收敛得到最优解。同时第二阶段的配水间位置优化又能对前一阶段的注水井组划分进行反馈，即若该注水井组划分方案下，所求得配水间最优位置远不能满足相关约束或者目标函数，则证明该注水井组划分方案较差。

2.2.1 方程确定

（1）适应度函数的确定。采用适应度函数作为衡量种群中个体优劣的唯一标准，适应度函数的选择会直接影响算法的收敛速度和最终的求解结果。在遗传算法中适应度函数要求为单值、连续、非负、最大化函数[16]。因配水间站址优化中目标函数为加权距离最小，因此需要对目标函数进行一定的转化以满足遗传算法对适应度函数的要求。若某种配水间站址方案不满足模型的某个约束条件时，需加入惩罚因子使该方案的适应度变低[17]，从而使得产生子代的概率减小，最终被淘汰，适应度函数的具体表达式如下：

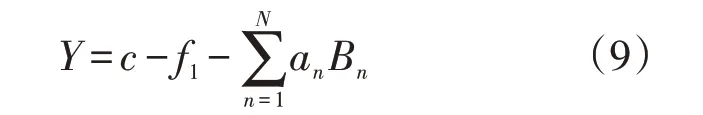
式中：an为不满足第n个约束条件的惩罚因子；Bn为判断某个解是否满足第n个约束条件的二元变量，若不满足则Bn=1，反之Bn=0 ；c为常数，通过设置合适的c值以保证适应度函数为正值。

（2）编码方式的确定。遗传算法的编码方式有二进制编码、浮点数编码、实数编码等形式，二进制编码较为常用，且对于注水井组的划分问题来说，二进制编码匹配性较好。该步骤需要根据配水间管辖注水井的数量要求确定大致的配水间数量。注水井与配水间隶属关系与算法编码对应关系如下：若某注水井属于某配水间，则对应编码为“1”，若不归该配水间管辖，则在对应位置的编码为“0”，之后将各注水井相对于各配水间的对应编码进行顺序排列；若注水井数量为n，配水间数量为m，则生成长度为n×m的二进制编码，一串二进制编码即为算法中的一个个体，代表一种注水井组的划分方案，如图2 所示。该编码方式较为直观，也便于后续的优化求解。具体求解过程中，注水井组划分方案即遗传算法优化中需要判别的约束有注水井隶属关系的唯一性约束［式（4）］、配水间管辖注水井的数量约束［式（5）、（6）］以及配水间管辖注水井的流量约束［式（7）、（8）］。若所确定的二进制编码，即GA中的一个个体不满足以上约束，则需在该个体的适应度方程中加入惩罚函数。

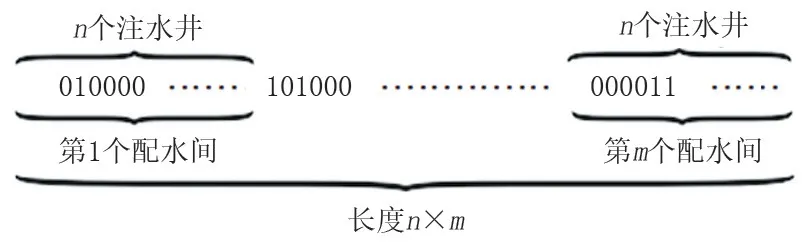
图2 注水井组划分方案编码Fig.2 Coding of water injection well group division

（3）选择算子。主要有适应度比例法、随机遍历抽样法和局部选择法。这里采用普遍使用的适应度比例法，是指按一定比例优选出适应度较高的即加权距离最小的注水井组划分及配水间站址优选方案，保证求解结果的经济性。

（4）交叉算子。随机将二进制编码中几个位于同一位置的编码进行交换，这里采用单点交叉方式，在编码串中设定一个交叉点进行交叉操作，两种注水井组划分方案以交叉点为界限，将前或后的部分编码串进行交换，以产生新的注水井组划分方案。

（5）变异算子。变异算子即父代方案里的某些基因按照一定概率变成对应的等位基因从而产生不同的子代。这里采用均匀变异的方式，即注水井组划分方案二进制编码串的每位基因都有一定的概率执行变异操作。

（6）最优保存策略。每代种群中按照一定比例选择适应度较高的个体作为父代（即经济性较高的注水井组划分及配水间站址优化设计方案），不需要进行交叉变异与模拟退火操作，直接进入下一代种群作为子代，以此提高模型的收敛速度。

2.2.2 求解步骤

采用SAGA求解注水管网布局优化中注水井组划分以及配水间站址优化方案的计算流程如下：

（1）首先确定初始参数，包括遗传算法[18]的种群大小、终止进化代数、交叉概率、变异概率；模拟退火算法的初始温度、终止温度、每个温度下的最大迭代次数。

（2）对于随机产生的注水井组划分方案进行二进制编码，产生遗传算法中的初始种群。

（3）将第k-1 代种群中的每种划分情况代入适应性函数进行评价。检查生成的编码是否满足管辖范围以及配水流量的限制，满足则保留，不满足则加入惩罚函数，加入惩罚因子使该方案的适应度降低，从而逐渐被淘汰。

（4）进行交叉变异操作，产生第k代种群。

（5）对于第k代种群采用模拟退火算法求解每种注水井组划分方案（每组二进制编码）中的配水间最优位置。具体流程如下：在某温度Tk下设定初始位置，将某一注水井组划分方案中各注水井的加权中心位置定为配水间的初始位置[9]，按照邻域函数在该位置附近产生新的位置，并分别计算初始位置与新位置的适应度，若新方案较优，则接受此方案；否则在0-1之间随机生成一个值，若此值小于，则接受此方案，否则保留原方案，当达到同一温度下的最大迭代次数后以一定的速度降低温度。当满足终止条件时，将最优解输出，计算结束。采用模拟退火算法求解配水间的最优位置过程中需要判别的约束主要有配水间管辖范围的约束［式（2）、（3）］。若所确定的配水间位置不满足配水间管辖范围的约束，则需要在目标函数中加入惩罚函数。每个注水井组划分方案下的最优配水间位置所确定的目标函数f1即为该个体的适应度值。

（6）重复步骤（3）～（5）直至达到终止进化代数或得到最优的注水井组划分及配水间站址优选方案。求解程序框图如图3所示。

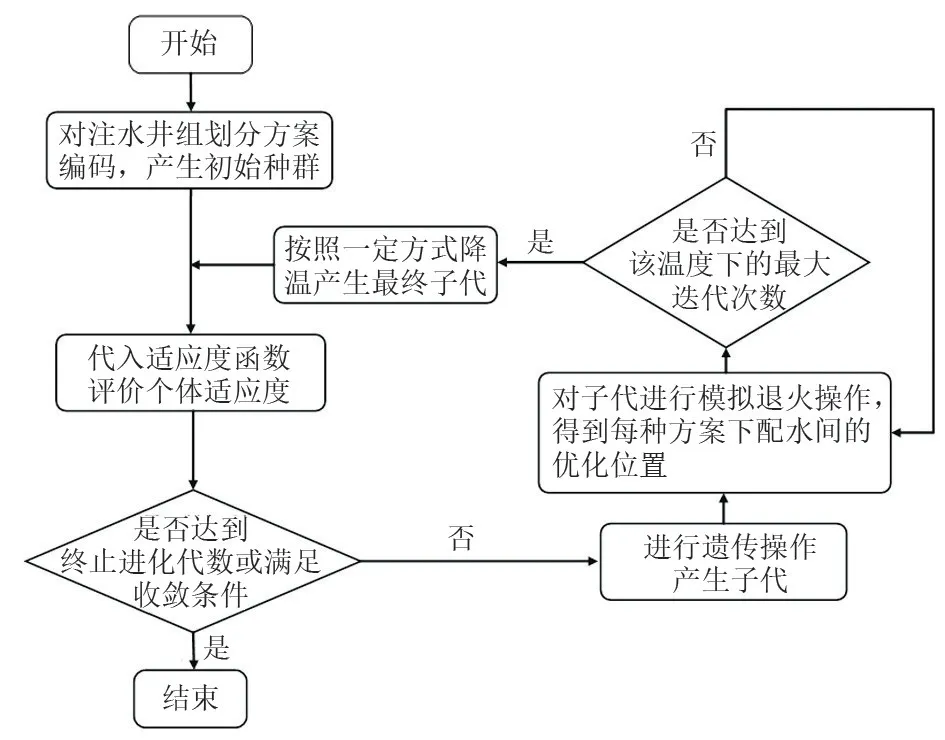
图3 注水井组划分与配水间位置优化算法流程Fig.3 Algorithm flow for division of water injection well groups and position optimization of water distribution stations

3 注水管网拓扑结构优化

本文采用Dijkstra 算法确定串接型枝状管网的拓扑结构[19-20]。

Dijkstra 算法是典型的求解最短路径的算法，较适用于油田注水管网拓扑结构优化[21]。采用该方法可以求得串接型枝状管网连接形式下注水站与各配水间相连管段加权距离最小的拓扑结构。

应用Dijkstra 算法[22]确定管网拓扑结构的具体求解步骤如下：

（1）指定计算的起点s，另外引进两个集合S和U。在计算初始状态时，注水管网的注水站及各配水间位置已经确定，将注水站位置作为拓扑结构的起点s并放入初始节点集合S中。依次计算s点与其他节点（各配水间）之间的管线建设费用，优选出加权距离最小的形式，将该形式纳入到注水管网的拓扑结构中，并将该配水间的位置顶点k 加入S集合中，同时从U集合中移除该顶点。

（2）以纳入S 集合中的新的节点作为起始点，选择出加权距离最小的连接形式纳入管网的拓扑结构中，更新S集合与U集合中的点。

（3）重复步骤（1）～（2），直到节点集合S将所有的配水间节点包含在内，形成最终的注水管网拓扑结构。

在采用Dijkstra 算法进行油田注水管网拓扑结构布局中，以“加权距离”作为管网建设投资的衡量指标，最终以此为基础确定了注水管网的连接形式以及优化得到的拓扑结构。

4 计算实例

整理大庆油田某区块注水井相关资料，得到注水井位置分布图，如图4所示；注水井注入流量信息，如表1所示。根据区块内所辖注水井数量，每口注水井所需注入流量以及注水站供水能力范围，将注水站数量定为1座，位置取所有注水井位置坐标的加权中心。采用以上提出的方法进行注水管网的布局优化设计。

在配水间位置优化中，算法基本参数配置如下：种群大小400，终止进化代数500，交叉概率0.85，变异概率0.005，精英个体保留比例10%，初始温度1 000，终止温度1，最大迭代次数100。采用MATLAB软件编程对模型进行求解。根据优化模型计算配水间最优位置，如图5所示。

图4 注水井位置及编号Fig.4 Water injection wells'locations and numbers

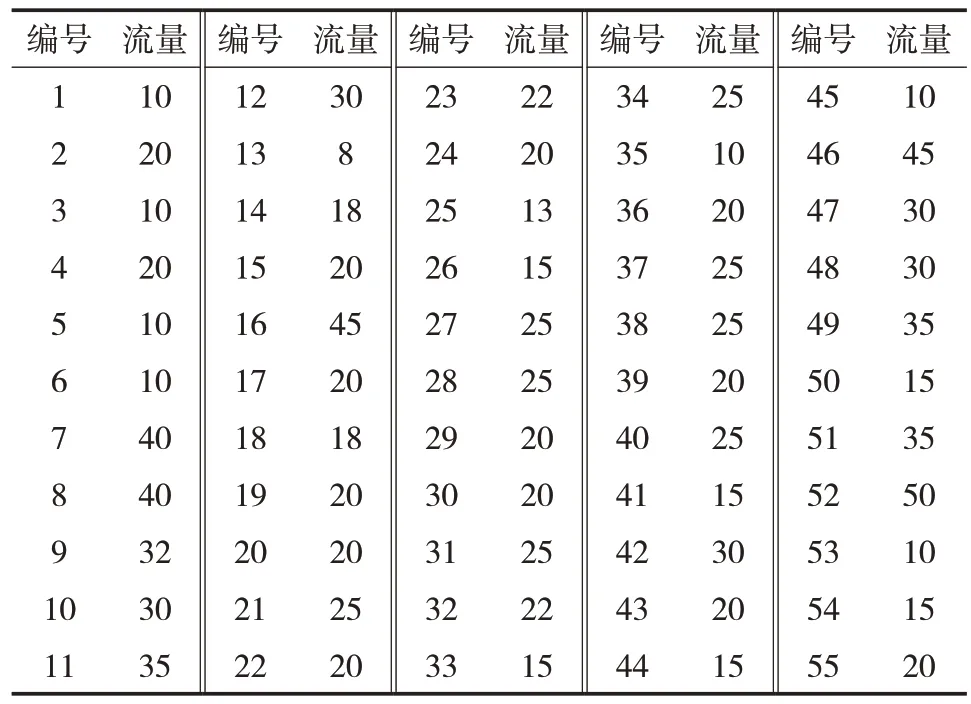
表1 各注水井注入流量Tab.1 Flow rate of each water injection wellm3/d

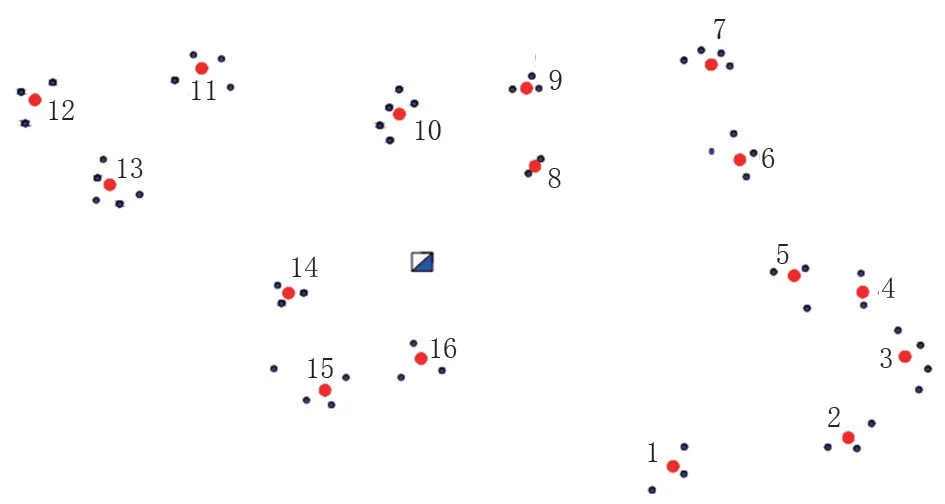
图5 配水间位置优化结果Fig.5 position optimization resurts of water distribution stations

在管网拓扑结构优化中，将流量以权重形式考虑在内，以管网内管道连接总长的加权距离之和w最小为目标函数，采用Dijkstra 算法得到注水站与各配水间连接管段加权距离最小的管网拓扑结构方案。w的具体表达式如下

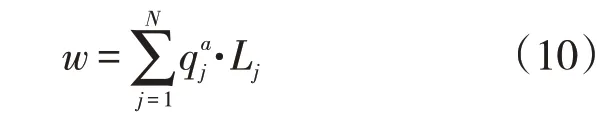
现场管网布局图如图6a 所示，经计算其w值为1 423.5m2.5/s0.5。采用Dijkstra 算法计算最终结果如图6c 所示，目标函数w值为1 269.4m2.5/s0.5，节约管网投资约10.8%。为了便于比较，另采用一般分级优化法进行计算，即首先采用加权中心法进行注水井组的最优划分及配水间最优位置的确定，其次以w值为目标函数确定树枝状注水管网的拓扑结构，最终得到的树状管网如图6b 所示，其目标函数w值为1 335.5m2.5/s0.5，相比原布局方案节约投资约6.2%，可知采用本文提出的方法较其他方法更易得到最优解，本文将注水井组的划分与确定配水间站址的耦合关系考虑在内，采用模拟退火遗传算法进行整体优化从而得到配水间的最优位置；其他分级优化方法分步确定注水井组划分方案与配水间的位置，最终计算结果受初始方案的影响较大，一般无法得到全局最优解。在该算例中，采用本文提出的方法可得到注水管网布局优化设计的经济方案，具有一定可行性。

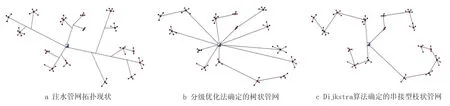
图6 注水管网拓扑结构对比Fig.6 Comparison of water injection network topologies

5 结论

本文在布局优化设计中，首先针对注水井区域划分及配水间的站址优化问题建立了混合整数非线性规划模型，配水间最优位置的确定受注水井组划分方案的影响，克服了一般分级优化方法较难得到全局最优解的弱点，采用模拟退火遗传算法进行分阶段求解，从而可确定配水间的最优位置；其次采用Dijkstra 算法，以注水站与各配水间加权距离最小为原则确定注水管网的拓扑结构，与现场及一般分级优化方法求解方案进行比较，本文提出的方法节省了注水系统投资，完成了科学、合理且经济的注水管网布局优化方案。在模型设计过程中将各节点间距离简化为两点间的直线距离，尚未将油田实际环境如地形地貌、障碍物等因素考虑在内，这将成为进一步的研究方向。