计及需求响应的综合能源系统优化运行策略研究

2020-11-17孙雅杰赵书健

吉林电力 2020年4期

孙雅杰，王贺，赵书健

(1.东北电力大学，吉林吉林 132012；2.国网吉林省电力有限公司电力科学研究院，长春 130021)

随着化石能源的过度开发，环境污染问题日益严峻，构建清洁、经济和高效的能源系统成为世界各国关注的重要问题[1-2]。在综合能源系统的运行优化研究中，很多学者对储能技术以及如何合理消纳风光出力进行了研究。为了平抑风力、光伏发电机组的出力波动，文献[3]通过用响应面法对蓄电池的容量进行优化，但由于使用寿命较短和环境污染较大，使蓄电池大规模应用受到限制。基于太阳日照强度和风能的波动性和不确定性，文献[4]在分析了光伏发电特性、风力发电特性和飞轮储能特性的基础上，提出了一种基于模糊控制的风能、太阳能及储能于一体的平滑控制方法来控制系统输出功率。为了提升综合能源系统运行经济性和稳定性，许多学者对系统的优化运行进行了相关研究。基于能源枢纽(EH)模型，文献[5]从多能互补的角度出发，提出了由能量枢纽运营商、用户和储能运营商三者共同组成的多能互补运行互动机制，接着建立了基于能量枢纽的主从博弈模型，并对其进行了仿真验证。文献[6]提出了一种含冷热电联产、光伏发电和地源热泵的分布式能源系统的优化运行策略，使系统的节能率和减排率得到改善。而上述研究均未考虑新能源发电同实际用电负荷在时间上存在相互不匹配的情况。

与上述研究不同的是，本文引入电解水制氢技术，用过剩产电量制取氢气，并储存在储气装置中参与系统需求响应，所产生的氢气还可为氢燃料电池提供燃料。因此本文首次引入新能源发电与负荷匹配度的概念来优化不同气象条件下系统的运行成本和二氧化碳排放量。

1 综合能源系统建模

1.1 综合能源系统结构

氢气是一种清洁能源，具有能热值高、稳定性好、便于储存和传输等诸多优点，将电解水制氢气技术应用到综合能源系统优化运行中具有广阔前景。

综合能源系统包含3个部分：供给环节，综合能源系统的能源来自风电、光伏、从外部购入的柴油和天然气；中间转换过程，热电联产(CHP)机组、燃气锅炉(GB)等能源转化设备实现多种能源之间的转换和互补；负荷终端，终端用户的热、电负荷需求以及储能装置。

1.2 各机组出力模型

a. 风力发电机组：

(1)

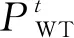
b. 光伏发电机组：

(2)

c. 电解槽：

(3)

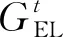
d. 氢燃料电池：

(4)

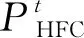
e. CHP机组：

(5)

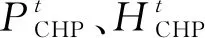
f. 燃气锅炉：

(6)

g. 柴油机：

(7)

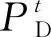
2 电力需求响应模型

2.1 电价模型

售电电价r(t)是和用电负荷等因素密切相关的，可以表示为：

(8)

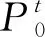
2.2 价格型电力需求响应模型

基于前文所提的电价模型，本章通过考虑价格型需求响应，将价格型电力需求响应模型表示为：

PL(t)=PL0(t)×

(9)

式中：PL0(t)、PL(t)为需求响应前后的负荷需求；r0(t′)为需求响应之前t′时刻的电价；r(t′)为需求响应之后t′时刻的电价；E(t,t′)为弹性因子，当t=t′时，表示自弹性(单一时段)，当t≠t′时，表示交叉弹性(多时段)。

3 目标函数及约束条件

综合能源系统的总运行成本Mc表示为各个机组的运行成本之和，即购买天然气成本Mpg、购买柴油成本MD、风光度电成本MW和MPV以及碳排放成本Mce的和，目标函数为：

minMc=Mpg+MD+MW+MPV+Mce

(10)

详细论述如下。

a. 购买天然气成本Mpg。综合能源网购买的天然气一部分进入CHP机组，另一部分进入燃气锅炉。设天然气价价格为定值，则购入天然气的费用可表示为：

(11)

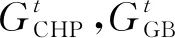
b. 购买柴油成本MD。综合能源网购入的柴油直接进入到柴油发电机中作为燃料。设柴油价格rD为定值，则购入柴油的费用可表示为：

(12)

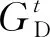
c. 风光出力发电成本MW和MPV。设风力和光伏发电机组的价格rWT和rPV为定值，分别取0.72元/(kW·h)和0.46元/(kW·h)，则风光出力发电成本可表示为：

(13)

(14)

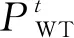
d. 碳排放成本Mce。本文所定义的总碳排放量由购入天然气的等效碳排放量和购入柴油的等效碳排放量两部分组成，令βD和βg分别表示柴油和天然气的等效排放系数，分别取0.26 kg/(kW·h)和0.24 kg/(kW·h)，ε表示单位质量CO2的处理费用(0.03 元/kg)，则碳排放成本可表示为：

(15)

4 新能源发电与负荷匹配度的含义、优化策略和优化算法

4.1 新能源发电与负荷匹配度的含义

光伏和风力发电受环境因素(光照、风速)影响较大，具有较强的随机性和不确定性。因此新能源发电同实际用电负荷在时间上存在相互不匹配的现象，进而导致弃风弃光。为研究新能源发电在时间上与负荷不匹配对系统运行的影响，本文首次定义匹配度φ为风力及光伏发电总出力与负荷的重叠部分和总负荷的比值。

4.2 优化策略

首先在给定的负荷数据与新能源出力曲线的特定情况下，即匹配度为固定值时，在计及需求响应前后对综合能源系统中电解水系统的能量交互情况和柴油机组的出力情况进行了分析。随后，在给定负荷下，研究了不同风光出力的情况下，即不同匹配度下系统的运行成本和二氧化碳排放量。通过分析电解水系统的能量输入与输出的动态变化，研究不同气象因素对综合能源系统运行的影响。

4.3 优化算法

使用自适应遗传算法(AGA)对综合能源系统运行进行优化是目前比较常用的方式，AGA通过自适应地调整交叉概率和变异概率，可以显著提高遗传算法的收敛精度和收敛速度。在用AGA进行寻优时，主要通过比较适应度函数值来区分每个个体的优劣，且在使用遗传算法进行求解时，适配值越大优化效果越好，因此为了获得最优的综合能源系统的运行成本，本文适应度函数用目标函数的倒数表示，同时选择综合能源系统中各组件每小时输出的功率为控制变量，通过AGA对系统的运行成本进行优化，算法优化流程图见图1。

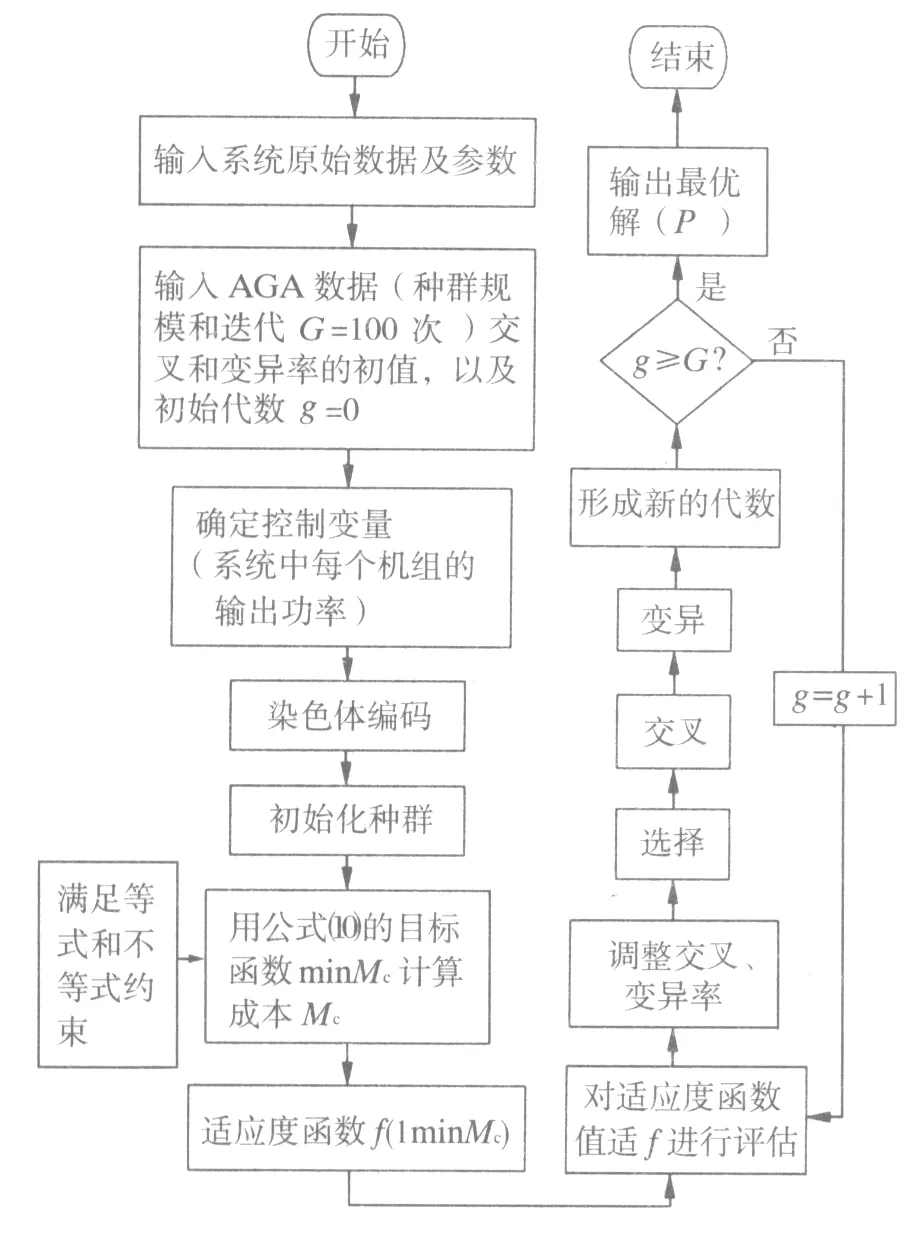
图1 AGA优化流程图

5 算例分析

5.1 场景描述和基本参数

本节以一个典型综合能源系统为例，对所提出的优化运行策略进行仿真验证。此外，考虑到储热水箱安装成本低廉，且回收余热有助于提升综合能源效率，所以假设该综合能源系统所配置的储热水箱容量能够完全收集余热。同时，氢气可通过高压压缩的方式实现大规模储存，假设电解槽电解的氢气可全部被存储在储氢装置中，高效地参与系统的需求响应。表1给出了负荷的弹性系数。

表1 电负荷弹性系数

通过对该综合能源系统中的负荷和气象状况进行监控，数据中心记录了日负荷数据和气象数据。某典型日的电、热负荷需求和根据所提的价格型电力需求响应模型计算出的参与需求响应后的电负荷需求见图2，该日风机和光伏的输出功率见图3。

图2 典型日负荷曲线

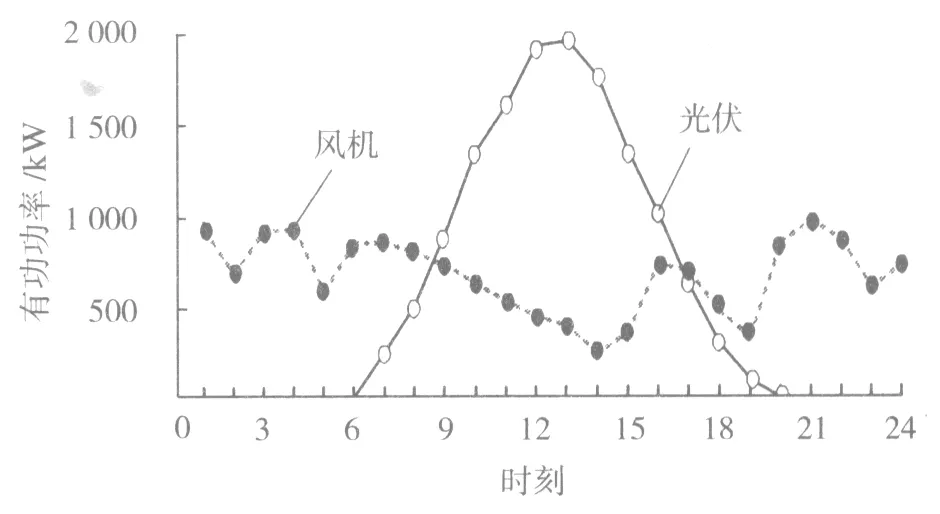
图3 典型日风机和光伏输出功率曲线

5.2 结果分析

5.2.1 需求响应前后综合能源系统优化运行结果

为了了解需求响应后综合能源系统中的电解水系统的能量充放情况，图4展示了电解水系统的实时能量交互(小于0表示储存能量，大于0表示释放电能)。从图4中可以看出，在考虑了需求响应后，电解槽在7 h和11～14 h进行能量存储，燃料电池在2 h、18 h和22～24 h进行电能的释放。根据计算得出：电解水系统能完全将3 532.85 kW·h的电能转化为氢气存储在储氢系统中，在用能紧张时刻可释放电能1 413.14 kW·h。这说明相较于不计及需求响应的综合能源系统，计及需求响应的系统中的电解水装置具备更高的灵活性，可以帮助系统解决一部分用能紧张的能量需求。

图4 需求响应后电解水系统的实时能量交互

需求响应前后的能源系统中柴油机组日出力情况作对比见图5，可以看出对于不计及需求响应的系统而言，柴油机组全天都在运行状态，而在计及需求响应后，柴油机组每天在7 h和11～14 h是可以不工作的，这是因为参与需求响应后的电负荷进行了转移或者削减，使得在这一阶段的负荷可由新能源发电满足，从而减少了柴油机组的出力。通过计算可知，计及需求响应后的综合能源系统柴油机的总发电量比不考虑需求响应的系统降低了约13.9%。与此同时，计及需求响应后的综合能源系统日运行成本也减少了约7.4%，其中碳排放成本降低了约7.6%。

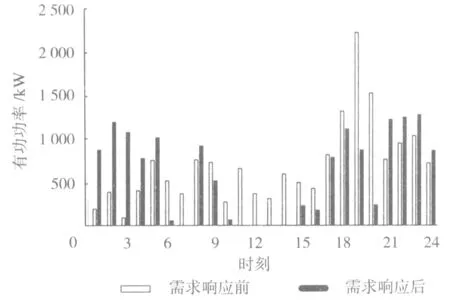
图5 计及需求响应前后综合能源系统柴油机组日出力

5.2.2 不同匹配度系统运行成本及碳排优化结果

为了揭示不同气象条件(风速、光照)对系统优化运行的影响，本节在确定的负荷需求(参与需求响应后的负荷)下，研究了不同匹配度下的最优运行成本、碳排量及电解水系统运行情况的变化。表2展示了负荷匹配度由50%上升到70%的过程中系统运行成本和碳排量的变化情况。

表2 运行成本和碳排量变化情况

由表2可知，随着负荷匹配度的升高，综合能源系统的运行成本和碳排量均呈现下降趋势。即当负荷匹配度从50%升到70%时，日均运行成本下降了约15.8%，碳排量降低了约35%。产生这种变化的原因是：随着负荷匹配度的升高，新能源发电的利用率越来越大，储氢系统所需转移的电负荷逐渐减少。通过对5种匹配度下电解水系统的能量交互进行计算可知，随着负荷匹配度的升高，电解水制氢的量逐渐减少，同时向系统释放的电能也越来越少。计算表明，当负荷匹配度由50%升至70%时，释放的总电能减少了约63%。这是由于随着负荷匹配度增加，新能源发电可以满足的负荷越来越多，因此电解水系统需要消耗的电能总量减少，参与需求响应的氢气也随之减少。