精馏过程稳态模拟计算方法分析

唐 强

（昭通市鼎安科技有限公司，云南昭通 657000）

1 稳态精馏过程的数学模型

整体分析，用于模拟精馏过程的数学模型主要包括如下几种[1]：

1）MESH 平衡级模型：该模型在实施过程中假定塔板上方浓度整体混合，并且脱离平衡级的两相流体之间建设了相位平衡关系，其通过联合建设物料均衡、相位平衡、热量平衡测算方式等诸多方式，获得不同塔板的流量、构成分布相关指标。

2）混合池模型与拓展模型：都假设塔板上浓度存有局部混合现象，基于物质、热量传送及对流的衡算情况实现求解。

3）基于计算流体力学与传质学建设的模型：通过联合建设得出与流动过程相配套的连续性方程与动量方程，在此基础上获得塔板上汽液相的实际速度与浓度分布状态相关数据信息，该模型还能精确计算出板式塔的默弗里板效率。

相比之下，基于MESH 方程组的测算流程较为简单，故而MESH 平衡级模型的应用范围更广。针对稳态精馏阶段的常规精馏塔模拟计算，由于各等级物料输入、输出状况大体等同，所以可以随意选取第j 平衡级（见图1）去表示整个精馏塔的运作状况。如果将组分数设定为c，那么便可以写出精馏过程稳态操作下对应的数学模型

针对物料建设的平衡对等关系，将其叫作M 方程，对图1内任一平衡级J 作为组分i 的物料衡算见式（1）[2]：

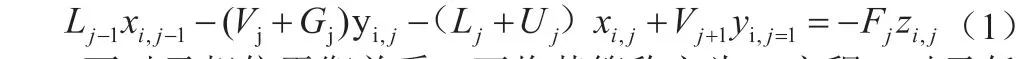
而对于相位平衡关系，可将其简称之为E 方程，对于任何一个组分而言，有式（2）：

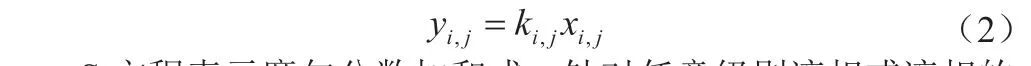
S 方程表示摩尔分数加和式，针对任意级别液相或液相的摩尔分数总和始终为1，则有式（3）：

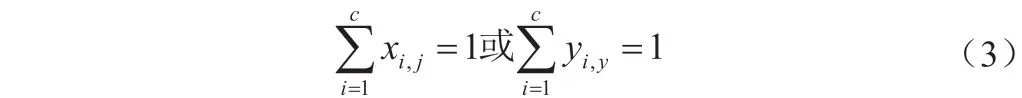
用H 方程表示热量平衡方程，针对任意一个理论级，进行热量衡算后能得到式（4）：

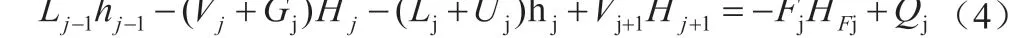
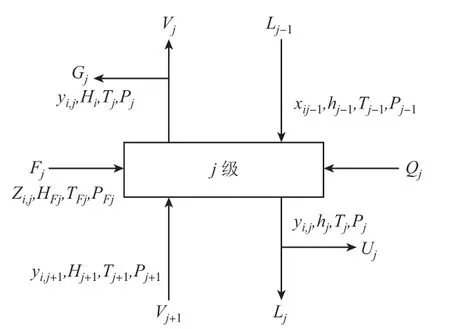
图1 第j平衡级

2 模拟稳态精馏过程计算方法的发展历程

2.1 三对角矩阵法

2N 牛顿-拉夫森法的基本思想可以做出如下概述：先对非线性方程组进行线性化处理，而后利用迭代法求出相应的结果。该方法在应用过程中，综合分析了塔板上的汽相流量、差异化塔板温度对熔平衡及组分加和方程形成的影响，故而该种方法在宽馏、窄馏分的分离测算领域中均表现出良好的适用性。但该法应用阶段暴露出最明显的缺点是测算量极为庞大，故而在非理想型偏强的体系内适用性非常差。方法计算量十分庞大，且不适用于非理想性较强的体系。Bennett J M[3]以此为基础做出针对性的改进后，规避数次求解偏导数与在单位层面上解离三角以及下三角矩阵。该法应用阶段仅测算单次Jacobian 矩阵，后期涉及的各次迭代对应的系数矩阵都可以采用上次迭代的矩阵捕获，迭代时间显著被压缩，收敛速率明显提升。

针对传统的自由度N（2C+1）同时校正法现实应用中暴露的不足，1997年王世怀等导入了以自由度N（2C+1）数学模型为核心的三对角线方程组联立法。该算法减少了模型方程与变量向量的维数，且对相位平衡常数与焓值均进行了回归处理，利用解析法把过往采用的差分法求一阶偏导数取而代之，同步提升了联立求解方程的运行效率与安稳性。

流量加和法是表示三对角矩阵的另一种特殊形式，其利用物料及相位平衡方程联合对汽液相流量进行校正处理，由焓平衡方程负责校正温度。该方法在首次迭代环节中要给定液相流量与温度值，而后算出汽相流量与相平衡常数，最后利用三对角矩阵测求出液相具体构成。H、S 方程分别用于校核温度与流量。如果确定新产生的液相流量、温度与原始值之间形成的偏差低于收敛准确度，则提示预期的收敛目标，反之则要返回持续进行循环迭代测算，直至抵达收敛为止。该种算法在吸收塔、宽沸程精馏系统内表现出良好适用性[4]。

2.2 牛顿法

可以将牛顿法看成是一种同时修正法，应用阶段一定要给出适宜的预测值作为原始值，从原始值开始就应用导数函数对变量向量的预测值加以分析，以此为基础生成一个和线性函数相似度很高且逐渐临近被解函数，基于测求近似函数的过程，循环迭代变量向量获得了被解目标函数的解。但其属于一种局部收敛法，对原始值提出较高的要求，且测算过程会耗用较长的时间。

张克诚等吸纳了三对角矩阵法、2N 牛顿-拉夫森法算法的优势，提出了联合算法，即三对角矩阵-2N 牛顿-拉夫森。该联合算法的应用原理可以做出如下表述：先采用三对角矩阵法测算获得相对较好的原始值，而后再将其整合到2N 牛顿-拉夫森法进行求解，并采用该算法测算到最后收敛。该种联合算法应用阶段最大的难点是确定最适宜的时间点切换两种算法，笔者结合既往经验做出切换算法时应遵照的依据。通过试验证实，联合算法在应用阶段表现出良好的稳定性，收敛过程也较为快速。

Vazquez-Esparragoza 等[5]建设了牛顿-拉夫森函数转换联合法，其在测求高度非线性方程组方面表现出良好效能，尤其是针对稀疏或者非稀疏体系时，该算法体现出简易性、高效性等特征。Estman，Kel-ly R 等提出了牛顿近似法，整合牛顿法与Schubea 更新，和局部牛顿法与Schubea 法相比较，其在应对精馏问题方面更具有效性、安稳性。该算法允许使用大批量现成的分析局部导数信息，并且针对那些获取难度系数较高的倒数采用取相似值的方法。在测算精馏物理性质方面，该算法耗用的时间明显短于牛顿法，大概是牛顿法用时的60.0%～70.0%，这主要是因为在现实测算中精细度较高的计算占比较高。但在获取等同的精确度时，该种方法的迭代频次通常要多于牛顿法。

2.3 内外层法

Boston J F 等是内外层法的提出者，再次对能量与挥发度相关参数做出定义是建设该算法的重要基础。为消除某一相互干扰，于各级别上定义首个第三参数，将该参数设定为汽液相流率与温度形成的特有整合体，采用前期修整好的拟牛顿法对这些参数进行迭代处理。该算法应用阶段省略了对汽液相流率与塔板温度两项参数进行迭代处理的过程，明显提高了收敛速率，算法运行过程相对较稳定；但是在执行该算法过程中需联合使用诸多参数，故而计算流程较为繁杂。

2.4 松弛法

Rose 等提出松弛法的概念，其是以不稳定状态下的物料均衡为基础测算精馏的一类方法，其效仿精馏运行过程由波动态转向稳定态的过程进行求算。先选取各个塔板的原始构成，选用进料构成或他类方便测算的构成，而后采用非稳定态的物料衡算方程测算各块塔板，设定适宜的时间间隔进行测算以获得单组塔板上的液相构成，重复进行以上这种测算操作直至两个相毗邻的测算结果等同，提示塔板上的构成抵达了稳定态，迭代频次对应的是测算时间。

宋海华等把松弛法和修正后的N-R 相整合，研发出实用性较高的通用型算法-联合算法，该算法采用稳定性较高的松弛法开展测算工作，等到收敛结束后转到N-R 法迅速完成收敛测算，在以上过程中无须用户设定不同算法的转向时间。基于实际案例证实，该种算法应用阶段表现出较好的安稳性，收敛速度也很快，可以被看成是一种理想度较高的模拟计算方法[6]。李天一等提出建设复杂精馏塔的数学模型，而后采用松弛法和N-R 法联合算法求解模型。应用实例表明该算法对初始值没有提出较高要求，且收敛过程稳定性较高。

3 不同计算方法的优劣势对比分析

牛顿法的适用范畴较宽，能快速收敛，但对原始值提出较高要求，原始值和现实解邻近度较高时，该法计算精馏过程能取得良好成效。但若初始值与真值间存在较大偏差时，利用该法测算很难实现收敛。内外层法明显地提升了收敛过程的安稳性，速度也显著加快，但面对高度非理想化体系时，其实现预期收敛目标的难度较高。经修整以后得到的内外层法对原值没有提出较严格的要求，拓展了自身使用范畴，减少了内存占用率，且还能取得精确度较高的计算结果。松弛法对原始值提出的要求偏低，收敛过程较为迟缓，适用于模拟测算非理想化物系的稳态式精馏过程。

对多种用于模拟计算稳态精馏过程的算法优势、弊端进行分析后，能清楚地感知到每个算法均有一定适用范围及优点与不足，当下尚无一种方法能聚集多个优点于一身。故而，在处置现实的精馏问题时，应依照各种测算方法的特征选用适宜度更高的方法模拟计算精馏过程。

4 结束语

综合本文论述，能清楚地感知到现存的稳态精馏过程模拟计算法适用测求类型均有一定适用范围及优点与不足，难以断言哪种算法占有绝对性优势，故而当前其均有一定应用，但依然没有开发出一种完美的计算方法去应对稳态精馏过程模拟计算的现实问题，相关模拟计算方法还有很大改进空间。