基于现场数据的城轨计轴设备可靠性评估

2020-11-17宋晗炜

北京交通大学学报 2020年5期

牛儒，宋晗炜

(北京交通大学 a.轨道交通控制与安全国家重点实验室，b.电子信息工程学院，北京 100044)

城市轨道交通信号系统中，计轴是检查、判断轨道区段的列车占用与出清的重要设备[1].由于其安装调试方便，不受轨面污染、隧道潮湿等环境因素影响，因此很快替代传统的轨道电路广泛应用于CBTC系统以及FAO系统中.计轴设备故障时，联锁系统无法获取正确的进路占用信息，出现“异常占用”现象.一般情况下，需要人工确认进路空闲、复位等一系列操作才能放行列车，造成不必要的延误.此时如果叠加列控系统的其他故障(前次列车是非通信列车或待通过列车是非通信列车)，则需要列车以目视模式清扫故障区段或引导接车，极易造成5分以上晚点，甚至交通瘫痪.而且，上述故障处置需要人工替代设备完成安全关键的进路占用检查工作，引入人误风险，增加系统安全隐患.因此，计轴设备的可靠工作对于高密度、小间隔的城市轨道交通的安全、高效运营至关重要.

然而，目前我国多条城轨线路故障数据显示计轴设备故障在信号设备故障中的占比居高不下.据统计，南京地铁反复出现计轴紫光带，板件死机等问题，其故障占整体轨旁故障的53%.广州、北京等地的城市轨道交通中也出现了类似问题.计轴故障频发已经成为影响信号系统可用性，造成运营延误的重要问题.可见，分析计轴设备在真实工况下的故障原因，提升计轴设备可靠性是城轨信号系统亟待解决的问题.

可靠性分析主要包括机理模型方法和统计模型方法[2].机理模型方法是通过失效机理分析，来证明该失效设备的失效致因符合某种失效分布的物理背景[3].文献[4]根据对绝缘栅双极性型晶体管失效机理的分析结果，构建了寿命预测模型.文献[5]分析了结构系统在静载和疲劳载荷作用下的失效机理以及各失效模式之间的相关性,给出了在静载和疲劳载荷作用下结构系统的可靠性分析方法.文献[6]采用故障模式及影响分析(FMEA)法，将以可靠性为中心的维修理论应用到计轴设备维修中，确定合理的维修方式.然而，设备失效机理复杂，而且设备运行条件千差万别、故障致因分析难以全面，真实失效分布可能与理论模型存在较大差异.统计模型方法是基于寿命统计数据的概率分布，并利用假设检验方法检验结果的可用性.文献[7]运用统计分析方法对地铁关键系统进行了可靠性分析.文献[8]提出了一种基于极大似然法对电器产品的寿命失效数据进行可靠性分析.文献[9]构建了计轴检测盒的可靠性框架,定量地对其进行可靠性分析.但是，此类方法的有效性依赖于统计数据的质量.如果存在统计时间过短、数据不足或噪声过大等问题，可能无法拟合出有效的概率分布[10].

因此，本文作者提出了一种机理模型辅助的现场数据统计模型分析方法，根据机理分析结果筛选失效分布类型，运用统计模型思路估计分布参数，检验拟合优度选择最佳失效分布.首先对计轴的故障模式和故障机理进行分析，论证计轴设备失效可以看作随机事件、存在统计规律.然后，对杭州某地铁线路的计轴故障数据进行可靠性分析，得到最佳失效分布，并通过实际统计特征与预计统计特征的差异推断计轴系统的故障原因，提出维护和设计改进建议.

1 计轴失效机理分析

1.1 计轴的结构与工作原理

计轴系统集传感器，通信传输，故障-安全计算机等技术为一体，如图1所示.室外部分完成对信息的感应和采集传输处理；室内部分完成轴数计算及所检测区段的空闲与占用判别，输出处理等.

列车从检测区间的一端出发进入区间经过计轴点时，运算单元对传感器产生的轴信号进行处理、判别及计数，轨道继电器落下.发车端将“驶入状态”及“计轴数”等信息进行编码并不断发送给接车端.当列车驶出区间经过接车端计轴点时，接车端对传感器产生的轴信号进行处理、判别及计数，接车端将“计轴数”及“驶出状态”等信息进行编码传给发车端.两端对“计轴数”及“驶入、驶出状态”信息校核无误后两端轨道继电器吸起，给出检测区间的空闲信号.

1.2 计轴的失效机理

据现场调研和数据分析，计轴不同组件的部分失效机理如表1所示.

表1 计轴部分失效机理

从表1中可看出计轴设备的失效机理大部分为老化、磨损等，属于随机失效.因为这些原因的随机特性，硬件在何时发生随机性失效是无法预测的，但遵循概率分布，可通过可靠性或者分析得到失效率；当然，也有一些是由人为失误或外单位施工引起的磁头受扰，软件设计引起的失效，以及雷击干扰等环境因素引起的计轴受扰，属于系统性失效，不能用概率来描述系统故障.本文只讨论随机性失效，采用统计模型方法进行可靠性分析.

2 可靠性评估方法

在失效机理分析的基础上，筛选出几种典型故障分布模型作为基本假设统计模型.同时对现场失效数据进行预处理.然后对预处理的数据进行参数估计，通过A-D和K-S拟合优度检验准则确定计轴的最佳分布模型.可靠性评估流程如图2所示.

2.1 筛选失效分布类型

结合常用寿命分布的应用范围[11]，可知计轴系统组件相应的寿命分布类型.磁头受扰等由突发事件引起的失效，与工作时间的长短无关，适合指数分布.设备磨损或性能衰减，一般符合正态分布.半导体器件产生的疲劳，比如计轴主机内部元器件产生的疲劳，可能为对数正态分布或威布尔分布.若产品某一薄弱环节出现故障而导致整个产品失效，例如计轴传输通道中电缆的老化，则可能为威布尔分布.因此，可以将指数分布、正态分布、对数正态分布、威布尔分布作为假设的失效分布模型.

2.2 数据预处理

为了提高分布拟合的准确性，首先需要对原始故障记录从准确性和有效性两方面进行预处理，完成数据审核、筛选、转化等工作.

由于目前城轨计轴故障记录大部分是人工记录，数据审核过程需要检查记录是否缺少关键信息(完整性)、是否存在重复多余的记录(重复性)、是否存在笔误(一致性).除了常规审核之外，还需要识别并剔除系统性故障(或称为非随机性故障).根据现场调研，导致计轴设备故障的系统性原因包括由外专业施工引起的故障，如工务小推车过计轴区段导致计轴磁头受扰；环境引起的故障，比如雷击干扰计轴磁头；软件故障，计轴终端工控机不能自动清理历史计轴存储信息等.

之后，对筛选后的数据进行转换.对于计轴这个可修复系统，寿命是指两次相邻故障之间的工作时间，即无故障工作时间.因此，将故障记录中的故障时间点信息转换为故障间隔时间，得到计轴的寿命数据.

2.3 参数估计

常见的参数估计方法有极大似然估计法、最小二乘法、贝叶斯估计等.

由于贝叶斯的参数估计需要先验知识，即将参数视为某种已知先验分布的随机变量，先验分布需要根据历史资料和经验信息等确定.在对计轴的可靠性分析中没有参数的先验知识可用，需要对其进行经典统计学的分析；最小二乘法是使估计值和观测值之差的平方和最小，能够最好地拟合样本数据，主要用来估计线性函数的未知参数；极大似然估计是从模型中抽取该n组样本观测值的概率最大，即概率分布函数或似然函数最大.最大似然原理比最小二乘原理更本质地揭示了通过样本估计总体的内在机理.因此本文采用极大似然法进行参数估计.

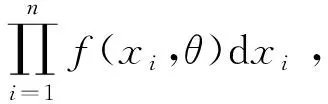
(1)

2.4 失效分布类型检验

分布检验是通过统计数据，推断寿命是否服从上文初步整理分析所选定的分布，推断的依据是拟合优度检验.拟合优度是寿命数据的分布与选定的理论分布之间符合程度的度量.其基本原理是根据样本对总体某项或某几项作出假设，并对该假设作出接受或拒绝的判断.本文对上述计轴寿命数据假定的四种分布类型进行检验，找到最佳分布模型.

常用的检验方法有K-S(Kolmogorov-Smirnov)检验和A-D (Anderson-darling)检验.

K-S检验能直接对原始数据进行检验，对数据的利用比较完整.K-S基本思想是将样本观测值的累计频率与假设的理论频率相比建立统计量.假设检验问题H0：样本所在的总体分布服从原假设，Fn(x)为其经验分布函数，提出检验假设的统计量为Dn=sup|Fn(x)-F0(x)|，根据样本观测值计算统计量D的观测值d,对于给定的显著性水平α和样本量n，得到临界值dn,α，当D≤dn,α时，接受假设H0；否则拒绝假设H0.

A-D检验的原理是将所收集的数据从小到大排列，得出经验累积分布并与目标分布的理论累积分布进行比较，得出A-D统计量，统计量越小，分布类型越拟合.A-D统计量的具体表达式为

(2)

采用Minitab，除了能计算出A-D检验的统计量之外，还可以计算出最小二乘法的Pearson相关系数.P相关系数是x和y之间线性相关关系强度的度量

(3)

相关系数γ取值在-1和1之间，γ的值越大(越接近于1)说明分布拟合得越好.

2.5 可靠性特征量

在确定模型的分布类型后，即可确定计轴的分布函数、分布密度函数和失效率等参数，进而对其可靠性进行评估.

可靠性特征量是用来评价设备可靠性的高低，是各种可靠性数量指标的总称.常用的可靠性指标包括可靠度、失效率、平均寿命和特征寿命.

失效率是描述产品可靠性规律的指标之一.失效率λ(t)与分布密度f(t)、分布函数F(t)以及可靠度R(t)的关系为

(4)

失效率函数与失效分布函数一样能够全面描述计轴寿命T的统计规律，它们之间是彼此相通的，只是各自强调的侧面不同.

对于可修复产品，平均寿命是指平均故障间隔时间(Mean Time between Failures, MTBF).

R(t)表示了产品在t时刻，能正常工作的概率值.但有时要知道为保证产品正常工作的概率要保持在某一水平R之上，产品可以工作的时间，即根据P{T>t}=R(t)=R，计算相应的时间t，该时间称为可靠寿命tR.可靠度R=e-1=0.368的可靠寿命称为特征寿命.

3 实例分析

以宁波地铁某条线路中的计轴设备的故障统计报表为基础数据.该条线路开通于2015年，全长28.35 km，其中地下线22.23 km、高架线5.77 km.正线双方向共布置计轴一百余个.

3.1 数据预处理与分析

首先对计轴故障统计数据进行筛选，去除非随机性故障以及明显不合理、错误的数据.而后，统计计轴的寿命.这里把计轴看成可修复设备，该线路的寿命数据是在线路运行过程中，两次故障发生的时间数据.由于随机性失效数据中包括不同计轴设备的故障数据，因此属于不同计轴的失效时间间隔需要从起始计数.得到的故障起始和故障间隔时间，如表2所示.

表2 计轴故障时间数据

将上述统计得到的寿命数据t按照从小到大的顺序排列为t1≤t2≤…≤tn.由于失效分布函数未知，采用经验分布函数Fn(t)代替总体分布函数F.采用近似中位秩计算经验分布函数.近似中位秩公式为

(5)

式中：i表示其排列的顺序号；n表示故障数量.表3为其对应的经验分布函数值.

表3 计轴故障时间与经验分布函数值

3.2 参数估计

对计轴进行可靠性定量分析，需要首先给出计轴寿命分布的参数估计，进而回答计轴的可靠性指标.参数估计包括点估计和区间估计.

采用极大似然估计法对基于失效机理分析筛选得到的4种假设分布进行参数估计.结果如下：

正态分布的均值为μ=445.9，区间估计为[284.1690,607.6310];方差为σ=345.568 3，区间估计为[262.8014,504.7273].

指数分布的λ=445.9，区间估计为[300.5643,729.9951].

对数正态分布的对数均值μ=5.745 1，区间估计为[5.3046,6.1855];对数标准差σ=0.917 3，区间估计为[0.6728,1.2505].

威布尔分布的形状参数为m=1.315 8，区间估计为[0.9279,1.8658]；尺度参数η=484.685 4，区间估计为[341.0386,688.8368].

3.3 假设检验

由于并不明确K-S和A-D两种方法对计轴寿命数据分布的检验效果，因此采用两种方法分别对数据进行检验，判断计轴的最佳寿命分布模型.

3.3.1K-S检验结果

用Matlab对4种分布进行检验.K-S假设检验的命令为：[H,s,ksstat,cv] =kstest(data,cdf).H为0接受原假设，H为1拒绝原假设；s为原假设成立的概率；ksstat为测试统计量的值；CV为是否接受假设的临界值.分析结果如表4所示.

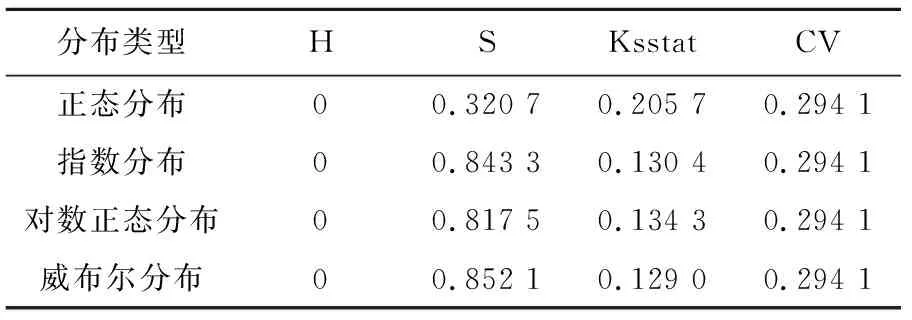
表4 四种分布的K-S检验结果

可见，4种分布均可满足K-S检验.除了正态分布的假设成立概率相对较低外，其他3种分布的成立概率接近.可见，对于实验数据而言，K-S检验的分辨度无法满足要求.

3.3.2 A-D检验结果

在Minitab软件的基础上完成A-D拟合度检验.A-D检验中的经验分布函数也是根据近似中位秩计算得到，如表4所示.

利用A-D检验法对数据进行检验，给出4种分布的概率图，如图3所示.它不是一种严格意义上的检验方法，且需要和其他检验方法联合使用[3].根据变量的累积概率对应于所指定的理论分布累积概率绘制的散点图，用于直观地检测样本数据是否符合某一概率分布.这些数据点若很好地分散在线性拟合直线的附近，则它对样本数据服从某种分布提供了粗略的支持.从图3可看出，对数正态分布和威布尔分布的线性拟合效果较好.

对于极大似然分布，A-D值越小分布类型越吻合；对于最小二乘法，相关系数越接近于1，分布类型越吻合.4种分布拟合结果的A-D值和相关系数如表5所示.威布尔分布和对数正态分布的A-D检验值和相关系数明显优于另外两种，且威布尔分布的A-D值最小，相关系数最接近于1.

表5 计轴寿命分布拟合优度

由表5可以看出威布尔分布与对数正态分布的假设检验结果相差不大，造成这一现象的原因包括两个方面：1)威布尔分布与对数正态分布在特定时间区域内允许有极为相似的概率密度；2)我国近几年才开始重视故障记录，有完整记录的线路运营时间有限.随着设备使用时间的增长、数据的丰富，该方法必然能够得到更加准确的结果，对运营和设计决策给出更可信的依据.

若计轴设备的寿命服从对数正态分布，其平均无故障工作时间(MTBF)为

这与威布尔分布下计轴的平均无故障时间(见3.4节)属于同一个数量级，二者相差不大.

因此，根据假设检验的最优结果即威布尔分布的假设检验结果略优于对数正态分布，将威布尔分布作为计轴寿命的分布类型.