素养导向下的高考数学
——新高考I卷(供山东省使用)试题分析
2020-11-16山东杨长智
山东 杨长智
新高考I卷(供山东省使用)试题是国家考试中心为山东省命制的高考试题(以下简称山东卷),试题以《普通高中数学课程标准(2017年版2020年修订)》(以下简称课标)为依据,以高考评价体系为准绳.命题突出数学学科特色,试题由能力立意向素养导向转变,试题稳中求变,变中求新,多项选择题、半开放试题的出现体现了课改方向.
笔者参加了教学考试杂志社“优师计划”一轮基础知识测评体系(山东省)项目,这个项目适用于新高考地区高三学生一轮复习阶段,其研发成果将作为一轮复习阶段的基础知识检测, 对一轮复习阶段的学习成果进行检验,故项目整体研发逻辑是构建一个完善的知识体系,并拟定以原创试卷的形式结合测评体系,检测学生在一轮复习阶段知识的薄弱点,实际高效地帮助学生夯实基础知识,为二轮复习奠定基础.
本文将从试题特点、项目匹配度、内容主线、思维维度、教学启示等方面对山东卷进行分析.
一、试题特点
1.在题型和试卷结构上进行了调整
山东卷的题型结构为8个单选题,每题5分,共40分;4个多选题,每题5分,共20分;4个填空题,每题5分,共20分;6个解答题,共70分,其中有一道半开放试题.
原来高考题中单纯的单项选择题,存在着一定的猜测几率,而多项选择题,可以考查学生对每个选项的思考,减少了答题的随机性,作为5分的选择题,学生得3分的较多,更容易得到基础分.多选题的多级得分模式有利于提高低水平考生的得分,也有利于区分出高能力考生.半开放试题的引入,增强试题条件的开放性,对数学理解能力、数学探究能力的考查能够起到积极的作用.
2.试题背景设置彰显立德树人的育人目标
山东卷强调应用背景与前沿问题、现实及体育、劳育的衔接,第4题日晷问题将传统文化与立体几何完美结合;第6题再生数与“抗疫”结合;第12题信息熵与科技前沿联系;第5、15题分别考查了体育、劳育;第19题环保问题让学生意识到保护环境的重要性.从试题的背景来看,引导学生关注社会,坚持立德育人.
3.注重数学理性思维,突出数学本质
山东卷注重对数学理性思维的考查,第7题正六边形中的数量积问题,考查了数量积的运算法则,利用坐标运算更加接近问题的本质;第17题半开放试题,学生选择可能不同,但考查的都是三角形中边角的数量关系;第22 题椭圆问题,对数学本质的考查更加到位,从角度为直角可以得出直线恒过定点.
4.从能力立意向素养导向转变,突出对核心素养的考查
22道题目,每道题都对数学运算进行了考查,虽然高考提倡“多一点思维,少一点运算”,但不可否认,运算关仍然是制约学生成绩提高的关键因素.直观想象不单纯是在立体几何中考查,在第8,10,18题的函数、三角、数列中也有所体现.
二、项目匹配度
从项目的考点细目表来看,设置内容包括知识点的考查、试题的呈现方式、试题结构、试题情境、数学思想方法、核心素养的落实及试题的难度系数等方面.从对山东卷的分析可以看出,我们的项目与国家命题中心的思路完全吻合.
1.知识点分布依据全国卷及新高考地区的考频特点分布,整卷涉及知识点数不少于40个.
2.题型与结构
单选题8道、多选题4道、单空题3道、多空题1道(虽然今年高考没有此题型,但近几年的高考中都显露出此信息)、解答题6道.
3. 试卷命题素材
命题情景创设(素材选择)标准:坚持科学性、反映时代性、体现民族性并凸显公共性.素材本身无科学性错误,不存在由于学生生活环境偏差导致的不公平测量结果的可能.素材主题积极向上,弘扬民族精神.
4.试题情境
试题情境可分为课程学习情境、探索创新情境、生活实践情境.
课程学习情境:选取的情境型材料直接源于学生已有的数学课程学习,材料所隐含的知识与方法之间的关联也为学生所熟悉,相应的情境活动的进行直接源于已有知识与方法的回忆性再现.
探索创新情境:选取的情境型材料源于学生已有的数学课程学习,但材料的表述方式、材料所隐含的知识与方法之间的关联,较为隐形地源于学生的已有学习体验或学习储备.相应情境活动的进行必须依赖于材料的创造性解读与转换、相关方法的创造性迁移与运用.
生活实践情境:选取的情境材料源于实际的社会生活问题(包括衣食住行、卫生健康、文体娱乐、生产制造、经济发展、科学技术等方面),材料所隐含的数学知识和方法、数学问题模型的建构和解决都较为直接地源于学生已有的学习储备.
从山东卷分析可以得出课程学习情境题15道,探索创新情境题3道,生活实践情境题4道,与 “优师计划”项目中试题的设置大致相当.
三、内容主线
课标将高中知识内容分为预备知识、函数、几何与代数、概率与统计、数学建模活动与数学探究活动几个方面,按四基中基础知识层次,各部分设置分值如下表:

题号内容分值知识点 预备知识(课时:18)函数(课时:82)几何与代数(课时:86)概率与统计(课时:46)1集合52复数 53排列组合54立体几何55统计56函数57向量58函数59圆锥曲线510三角函数511不等式512概率513圆锥曲线514数列515三角函数516立体几何517三角函数1018数列1219概率1220立体几何1221函数1222圆锥曲线12分值合计15595422分值占比0.10.3930.360.147课时占比0.0780.3530.3710.198
从上表可以看出,教学内容与高考考查对应分值占比大致相当,这就提示我们在平时教学时,夯实基础知识,落实通性通法,不要为赶进度压缩课时,造成“夹生饭”现象.
四、思维维度
对每道题目的分析主要从以下几个方面入手:知识点的考查、试题的呈现方式(文字题、图表文字题、图形文字题)、试题结构(单一、综合、创新或新定义)、试题情境(课程学习情境、探索创新情境、生活实践情境)、数学思想方法、核心素养的落实及试题的难度系数等方面.
(一)预备知识
1.设集合A={x|1≤x≤3},B={x|2 A.{x|2 C.{x|1≤x<4} D.{x|1 【答案】C. 本题考查了集合的并集运算,试题的呈现形式是文字题,试题结构单一,试题情境为课程学习情境,难度系数在0.9左右,体现了数学运算的核心素养. 5.某中学的学生积极参加体育锻炼,其中有96%的学生喜欢足球或游泳,60%的学生喜欢足球,82%的学生喜欢游泳,则该中学既喜欢足球又喜欢游泳的学生数占该校学生总数的比例是( ) A.62% B. 56% C. 46% D. 42% 【答案】C. 本题以体育锻炼为背景,考查集合内容,试题的呈现形式是文字题,试题结构单一,试题情境为生活实践情境,需要有一定的阅读理解能力,与韦恩图结合,考查了数形结合思想,难度系数在0.8左右,体现了逻辑推理、数学建模与数学运算的核心素养. 11.已知a>0,b>0,且a+b=1,则( ) 【答案】ABD. 本题以不等式为载体,对化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.7左右,体现了逻辑推理与数学运算的核心素养. 6.基本再生数R0与世代间隔T是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I(t)=ert描述累计感染病例数I(t)随时间t(单位:天)的变化规律,指数增长率r与R0,T近似满足R0=1+rT.有学者基于已有数据估计出R0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln2≈0.69) ( ) A. 1.2天 B. 1.8天 C. 2.5天 D. 3.5天 【答案】B. 本题与生物学融合,跨学科命题,考查指数函数与对数函数,试题的呈现形式是文字题,试题结构创新,试题情境为探索创新情境,基于新冠肺炎疫情初始阶段累计感染病例数的数学模型的研究成果,考查相关的数学知识以及从资料中提取信息的能力,突出数学和数学模型的应用,需要有一定的阅读理解能力,考查了化归与转化的思想,难度系数在0.6左右,体现了逻辑推理、数学抽象与数学运算的核心素养. 8.若定义在R的奇函数f(x)在(-∞,0)单调递减,且f(2)=0,则满足xf(x-1)≥0的x的取值范围是( ) A. [-1,1]∪[3,+∞) B. [-3,-1]∪[0,1] C. [-1,0]∪[1,+∞) D. [-1,0]∪[1,3] 【答案】D. 本题以函数的性质为载体,对数形结合、化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,对思维的考查要求较高,难度系数在0.6左右,体现了逻辑推理、数学抽象与数学运算的核心素养. 10.如图是函数y= sin(ωx+φ)的部分图象,则sin(ωx+φ)= ( ) 【答案】BC. 本题考查了三角函数的图象与变换,对数形结合思想进行了考查,试题的呈现形式是图形文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.7左右,体现了直观想象、逻辑推理与数学运算的核心素养. 14.将数列{2n-1}与{3n-2}的公共项从小到大排列得到数列{an},则{an}的前n项和为________. 【答案】3n2-2n. 本题考查了数列的通项与求和的公式,对化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.8左右,体现了逻辑推理与数学运算的核心素养. 本题以三角函数为载体,对数形结合思想进行了考查,试题的呈现形式是图形文字题,试题结构综合,试题情境为生活实践情境,在考查几何知识的同时,培养学生的数学应用意识,难度系数在0.6左右,体现了逻辑推理、直观想象与数学运算的核心素养. 注:如果选择多个条件分别解答,按第一个解答计分. 本题以三角函数为载体,题目属于半开放试题,选择权交给考生是个新意,充分体现了能力立意和情境创新的要求,对数形结合以及化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为探索创新情境,难度系数在0.7左右,体现了逻辑推理与数学运算的核心素养. 18.已知公比大于1的等比数列{an}满足a2+a4=20,a3=8. (Ⅰ)求{an}的通项公式; (Ⅱ)记bm为{an}在区间(0,m](m∈N*)中的项的个数,求数列{bm}的前100项和S100. 【答案】(Ⅰ)an=2n;(Ⅱ)S100=480. 本题以数列为载体,对函数与方程思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.6左右,体现了逻辑推理、数学抽象与数学运算的核心素养. 21.已知函数f(x)=aex-1-lnx+lna. (Ⅰ)当a=e时,求曲线y=f(x)在点(1,f(1))处的切线与两坐标轴围成的三角形的面积; (Ⅱ)若f(x)≥1,求a的取值范围. 本题以导数为载体,对分类讨论、化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.3左右,体现了数学抽象、逻辑推理与数学运算的核心素养. A. 1 B. -1 C. i D. -i 【答案】D. 本题考查了复数的除法运算,学生需掌握共轭复数的概念、复数乘法的运算法则,试题的呈现形式是文字题,试题结构单一,试题情境为课程学习情境,难度系数在0.8左右,体现了数学运算的核心素养. 4.日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O),地球上一点A的纬度是指OA与地球赤道所在平面所成角,点A处的水平面是指过点A且与OA垂直的平面.在点A处放置一个日晷,若晷面与赤道所在平面平行,点A处的纬度为北纬40°,则晷针与点A处的水平面所成角为( ) A.20° B. 40° C. 50° D. 90° 【答案】B. 本题以中国的传统文化日晷为背景,考查了线面角,对数形结合、化归与转化思想进行了考查,试题的呈现形式是图形文字题,试题结构综合,试题情境为生活实践情境,对阅读理解能力要求较高,难度系数在0.6左右,体现了逻辑推理、直观想象与数学运算的核心素养. A. (-2,6) B. (-6,2) C. (-2,4) D. (-4,6) 【答案】A. 本题考查了平面向量数量积,对数形结合、化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,对思维的考查要求较高,“多考一点想的,少考一点算的”,难度系数在0.6左右,体现了逻辑推理、直观想象与数学运算的核心素养. 9.已知曲线C:mx2+ny2=1.( ) A. 若m>n>0,则C是椭圆,其焦点在y轴上 D. 若m=0,n>0,则C是两条直线 【答案】ACD. 本题以曲线为载体,对数形结合、化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.7左右,体现了逻辑推理、数学抽象与数学运算的核心素养. 本题考查了直线与圆锥曲线的位置关系,对数形结合思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.8左右,体现了逻辑推理与数学运算的核心素养. 本题以立体几何为载体,题目涉及了直四棱柱、球、截面的有关知识,对数形结合、化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.3左右,体现了逻辑推理、直观想象与数学运算的核心素养. 20.如图,四棱锥P-ABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l. (Ⅰ)证明:l⊥平面PDC; (Ⅱ)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值. 本题以立体几何为载体,对线面关系及角的度量进行了考查,试题的呈现形式是图形文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.4左右,体现了直观想象、逻辑推理与数学运算的核心素养. (Ⅰ)求C的方程; (Ⅱ)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值. 本题以椭圆为载体,对函数与方程思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为课程学习情境,难度系数在0.3左右,体现了数学抽象、逻辑推理与数学运算的核心素养. 3.6名同学到甲、乙、丙三个场馆做志愿者,每名同学只去1个场馆,甲场馆安排1名,乙场馆安排2名,丙场馆安排3名,则不同的安排方法共有( ) A. 120种 B. 90种 C. 60种 D. 30种 【答案】C. 本题考查了排列组合,试题的呈现形式是文字题,试题结构单一,试题情境为课程学习情境,难度系数在0.8左右,体现了逻辑推理与数学运算的核心素养. A. 若n=1,则H(X)=0 B. 若n=2,则H(X)随着p1的增大而增大 D. 若n=2m,随机变量Y所有可能的取值为1,2,…,m,且P(Y=j)=pj+p2m+1-j(j=1,2,…,m),则H(X)≤H(Y) 【答案】AC. 本题以随机变量为载体,对化归与转化思想进行了考查,试题的呈现形式是文字题,试题结构综合,试题情境为探索创新情境,考查学生获取新知识的能力和对新问题的理解探究能力.难度系数在0.4左右,体现了数学抽象、逻辑推理、数学建模与数学运算的核心素养. 19.为加强环境保护,治理空气污染,环境监测部门对某市空气质量进行调研,随机抽查了100天空气中的PM2.5 和SO2浓度(单位:μg/m3),得下表: SO2PM 2.5 [0,50](50,150](150,475]32184[0.35](35,75]6812(75,115]3710 (Ⅰ)估计事件“该市一天空气中PM 2.5浓度不超过75,且SO2浓度不超过150”的概率; (Ⅱ)根据所给数据,完成下面的2×2列联表: SO2PM 2.5 [0,150](150,475][0,75](75,115] (Ⅲ)根据(Ⅱ)中列联表,判断是否有99%的把握认为该市一天空气中PM2.5浓度与SO2浓度有关? P(K2≥k)0.050 0.0100.001k3.8416.63510.828 . 【答案】(Ⅰ)0.64; (Ⅱ) SO2PM2.5 [0,150](150,475][0,75]6416(75,115]1010 (Ⅲ)有99%的把握认为该市一天空气中的PM2.5浓度与SO2浓度有关. 本题以统计概率为载体,对概率及列联表进行了考查,试题的呈现形式是图表文字题,试题结构综合,试题情境为生活实践情境,难度系数在0.7左右,体现了逻辑推理、数据分析与数学运算的核心素养. 1.落实《课标》教学目标,注重教学的有效性 《课标》指导和规范了整个高中教学过程,面向全体高中学生.在每部分内容的后面,设置了“教学提示”,教师要结合提示落实每节课的教学目标.在教学过程中既要关注全体学生的发展,又要注重高考选拔的要求,以学生为中心,注重教学的有效性. 2.夯实四基,提高运算能力 鲍建生教授指出:数学的四基是以认知模块的形式呈现出来的,在教学中要达到数学知识的积累、基本技能的演练、基本思想方法的形成,在三者的基础上,基本活动经验填充其中;学生能够在规定的时间内,准确的完成解题过程,这对数学运算的核心素养有着较高的要求,教师要在每一节课,给足学生时间,让学生动手、动脑. 3.注重能力发展,提升数学素养
(二)函数








(三)几何与代数






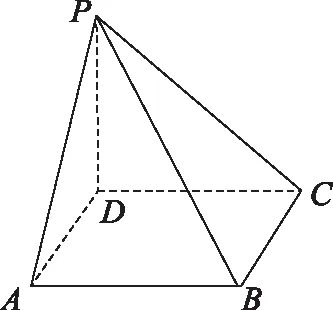


(四)概率与统计






五、教学启示

