基于半参数测量误差模型的加利福尼亚房价数据研究

娄 文

(南京理工大学 理学院，南京 210094)

0 引 言

在经济领域，研究地区房价与各种影响因素之间的关系有着较为重要的意义。何静等[1]利用可加模型对北京市二手房房价数据进行分析并通过分位回归方法对模型进行估计；周尔民等[2]根据江西省2005—2013年的房价数据,采用逐步回归分析法,建立多个房价回归模型,并对模型进行诊断和检验；尹雯雯[3]研究了变系数误差模型的核实方法在波士顿住房数据上的应用。研究的加利福尼亚房价数据集包含20 640个观测样本, 其中响应变量是中位房价(Median house value)，协变量包括中位收入(Median income)、房屋中位年龄(Housing median age)、总房间数(Total rooms)、总卧室数(Total bedrooms)、人口(Population)、家庭(Households)、纬度(Latitude)和经度(Longitude)。

在经济和医疗等领域，具有乘积扭曲结构的测量误差十分常见。entürk和Müller[18]在研究协变量和响应变量都含有乘积扭曲测量误差的线性回归模型时，提出了协变量调整回归(covariate-adjusted regression，CAR)。该方法通过建立回归系数与变系数回归模型之间的联系，消除了乘积扭曲测量误差给回归系数估计带来的影响，他们证明了利用协变量调整回归获得的回归系数的估计量具有相合性，并用此方法分析了血液透析患者的纤维蛋白原水平与其他血浆蛋白水平(如转铁蛋白水平、铜蓝蛋白水平和酸性糖蛋白水平等)之间的关系;Delaigle等[19]进一步讨论了非参数协变量调整回归的相关问题，在弱化了一些有关变量和扭曲函数的假设条件后，给出了更为灵活的非参数估计量，能够在协变量和响应变量期望为0或扭曲函数不满足严格大于0的条件下对非参数部分进行估计。

本文利用单指标扭曲测量误差模型对加利福尼亚房价数据进行拟合。由于单指标模型可以通过部分线性单指标模型退化得到，因此我们利用Zhang[20]提出的估计方法来进行模型估计。

1 模型介绍

参数回归模型最大的特点在于假设模型的结构是已知的，即响应变量和协变量之间的函数关系是已知的，仅有有限个参数未知。在这样的假设下，参数回归模型的估计问题就等同于这有限个未知参数的估计问题。因此，诸如线性模型和广义线性模型等参数回归模型的估计方法相对简单。参数回归模型对模型结构的假设除了给模型估计带来了便利，还提高了模型被错误识别的风险。如果模型与实际情况相符，那么做出的统计推断则有着较高的精度。一旦模型与实际情况偏差较大，获得的估计结果会很差。

非参数回归模型没有给出完全已知的模型结构，而是通过未知函数来构建Y与X之间的关系，所以适用的范围要比参数回归模型广泛。非参数回归模型在协变量的维数是一维的时候，得到的未知函数的估计精度较高，而当协变量的维数超过一维的时候，得到的未知函数的估计精度会随着维数的增大快速下降。这是因为诸如N-W核估计法(Nadaraya-Watson)、局部多项式估计法(Local Polynomial)和B样条估计法(B-Spline)等非参数估计方法(即光滑方法)的本质是局部光滑，只有确保某一点的领域内有着足够多的数据点，才能得到未知函数在该点较为精确的估计。然而，随着协变量维数的增大，一个局部领域内的样本个数占总的样本个数的比例会越来越小，局部光滑所需要的数据点个数成指数倍增加，这就是所说的“维数祸根”(curse of dimensionality)现象。

半参数模型在保留非参数回归模型优点的同时对协变量进行降维，较好地解决了“维数祸根”问题。该模型能够根据数据来确定模型的最终结构，能够很好地解释协变量与响应变量之间的影响关系，能够减小假设模型与真实模型存在偏离时的影响。经过不断地发展，半参数回归模型的形式也越来越丰富，包括部分线性模型、单指标模型、变系数模型和单指标变系数模型等，这些模型都已经广泛地应用于经济和医疗等领域。

在实际应用中，能够影响变量观测准确度的因素有很多，例如测量仪器自身的准确度不足产生的误差，使用测量仪器观测时读数产生的误差和获取各个样本的外部环境条件存在差异产生的误差等。如果忽略这些影响因素，默认变量的观测值与其真实值之间不存在偏差，利用半参数回归模型对含有测量误差的变量进行统计推断，那么推断的结果将存在偏差，严重时可能与真实情况完全违背。目前，测量误差影响观测值的方式主要有两类：一类被称为可加结构的测量误差模型，顾名思义就是测量误差以加和的形式影响真实值的观测，如W=X+U(W是观测值，X是真实值，U是测量误差)；另一类被称作乘积结构的测量误差模型，即测量误差以乘积的形式影响真实值的观测，如W=XU(W，X，U的含义同上)。

随着不断深入的研究，测量误差对于观测值的影响方式越来越复杂，简单的乘积结构的测量误差模型无法在某些复杂情况下进行有效的纠偏。因此，乘积结构的测量误差模型有了更为复杂的扩展形式，例如乘积扭曲结构的测量误差模型，W=Xψ(U) (W，X的含义同上，U是混淆变量，ψ是未知扭曲函数)，乘积单指标扭曲结构的测量误差模型，W=Xψ(θTU) (W，X，U，ψ的含义同上，θ为未知的指标系数)。在经济和医疗领域，诸多变量都具有乘积扭曲结构的测量误差。经济领域的房屋年龄和医疗领域的身体质量指数(BMI)等通常被视作混淆变量。

根据加利福尼亚房价数据的特点，房屋中位年龄可能作为混淆变量影响其他变量的观测结果。为了能够让模型尽可能地符合数据的实际情况，选择单指标扭曲测量误差模型对该数据进行拟合。

2 模型估计

单指标扭曲测量误差模型具有如下形式：

(1)

(2)E{ψ(U)}=1，E{φr(U)}=1，r=1,2,…,p。

假定式(1)是为了保证参数β0的唯一性。假定式(2)确保了乘积扭曲测量误差问题的可识别性，即从均值的角度来看乘积测量误差对变量无影响。这是一般情况下测量误差问题都需要满足的假定条件，其思想类似于经典的加性测量误差问题W=X+u中，假设E(u)=0来保证可识别性。

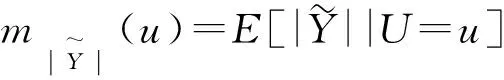
其中:

是核函数，h1是带宽。将响应变量和协变量的观测值与其各自对应的扭曲函数估计值相除，获得了校准后的变量：

利用条件绝对均值校准方法来对乘积扭曲测量误差进行纠偏可以看作是在对真实模型进行估计前的数据预处理。根据响应变量和协变量的观测值，采用核光滑来得到扭曲函数的估计量，再通过简单的相除运算得到响应变量和协变量真实值的估计，即校准后的响应变量和协变量。在进行模型估计的时候，使用校准后的响应变量和协变量代替观测到的响应变量和协变量。这样一来，就完成了对乘积扭曲测量误差的纠偏。

(2)

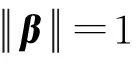
通过简单的计算，可以得到β关于β(r)的Jacobian矩阵:

g(T)≈g(t)+g′(t)(T-t)≡a+b(T-t)

得到的a和b的估计量，h是带宽。

根据最小二乘理论，可以得到：

其中：

通过求解方程组：

3 模型拟合

本文研究的加利福尼亚房价数据可在http://lib.stat.cmu.edu/datasets/houses.zip获得。运用单指标扭曲测量误差模型对该数据进行拟合，选取其中的中位房价(Median house value)、中位收入(Median income)、房屋中位年龄(Housing median age)、总房间数(Total rooms)、总卧室数(Total bedrooms)和人口(Population)这6个变量进行研究。各变量与其对应的符号表示如表1所示。

表1 房价数据变量Table 1 The variables of housing prices data

首先对表1的6个变量进行标准化处理，然后选取模型估计所需要的3个带宽h，h1和h2。带宽h1用于对扭曲函数进行估计，h和h2用于对未知函数g(·)和g′(·)进行局部线性估计。

(3)

来选择h,其中

因为这确保了满足最优渐近性质所需要的带宽有着正确的数量级，选取的结果为

h1=0.305，h=0.145，h2=0.430

根据上一节介绍的模型估计方法，给出估计模型式(1)中的未知指标系数β0和未知联系函数g0(·)的具体步骤：

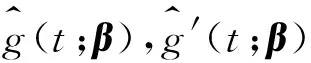
这里有一点需要注意，那就是非线性优化的收敛速度对初始值较为敏感。在某些情况下，广义线性模型能够帮助我们获得β0的初始值。但是当联系函数为指数函数或者三角函数的时候，就不能再通过广义线性模型得到初始值。此时，可以采用切片逆回归方法或者最小平均方差方法来获得β0的初始值。

根据加利福尼亚房价数据，依照上述算法，计算单指标扭曲测量误差模型的估计结果,最终得到的扭曲函数ψ(·)，φ1(·)，φ2(·)，φ3(·)和φ4(·)的估计结果如图1—图5。如果中位房价、中位收入、总房间数、总卧室数和人口不受到以房屋中位年龄为混淆变量的乘积污染，那么扭曲函数的估计曲线应该近似与直线Y=1平行且在该直线的附近。

观察图1—图5发现5个扭曲函数的估计曲线既不平行于直线Y=1，也不在该直线的附近。这验证了一开始的想法，在一定程度上说明了中位房价、中位收入、总房间数、总卧室数和人口受到了以房屋中位年龄为混淆变量的乘积污染。

表2 两种方法得到参数β0的估计Table 2 The estimation of β0 by two methods

4 结 论

经典半参数模型中大多数假设响应变量和协变量是可以准确观测的，这样能够简化模型。但是在实际应用中，数据存在测量误差的情况时有发生，尤其是在经济领域。忽略测量误差的影响，直接对模型进行估计会导致获得的结果存在偏差。针对加利福尼亚住房数据，选取房屋中位年龄作为混淆变量，采用单指标扭曲测量误差模型对该数据进行拟合。观察扭曲函数的拟合曲线后发现中位房价、中位收入、总房间数、总卧室数和人口均受到了以房屋中位年龄为混淆变量的乘积污染。这说明了所选择的单指标扭曲测量误差模型相比于不含测量误差的半参数模型更适合加利福尼亚住房数据。