资金约束下的工业共生链碳减排演化博弈分析

丁黎黎 ，张凯旋 ，王 垒

（1. 中国海洋大学 经济学院，青岛 266100；2.中国海洋大学 海洋发展研究院，青岛 266100）

党的十九大再次强调推进新型工业化建设，实现工业的高质量发展。虽然，我国工业降耗减排取得了令人瞩目的成绩，2018 年的单位工业增加值能耗比2013 年初下降了30.12%，二氧化碳排放的强度下降约32%，但是在工业废弃物循环利用方面，我国还有很大的提升空间。2019年的统计数据显示：大、中城市一般工业固体废物综合利用率仅为42.5%。在传统工业生产链条中，废弃物处理是以无害化为核心的末端治理，并不能高效利用废弃物资源［1］。以资源化、生态化为核心的工业共生链应运而生。工业共生链作为一种有效提高工业废弃物利用率的工业生态系统，工业共生链条上的主体通过工业循环原料的媒介形成了经济效益的合作、碳减排社会效益的协同，体现出了明显的共生关系特征。

工业共生链中的企业通过资源共享或者资源互补，大幅提高资源利用率［2］。例如，上游制造商对废弃物进行技术处理，使其作为下游制造商的生产材料，从而最大化地利用废弃物，直接减少生产材料的投入，使得污染物排放减少。然而，进行物质和能量的交换需要投入大量的成本，如管道、运输、人工、仪器仪表等［3］。以位于阿尔及利亚东北部的建筑共生网络为例，在Fil-Fila采石场中，大理石制造商的生产残渣经加工可用于混凝土生产，废弃物的运输、储存以及加工转化成本约为68 910欧元，虽然后期经济回报可观，可带来的经济收益高达约68万欧元，但是因其科技投入见效慢以及市场存在不确定性，银行不愿意为其提供贷款［4］。工业企业的融资难困境，已经严重制约了其节能减排的技术投入，成为制约工业共生链形成的重要障碍。

当制造商无法获得银行的资金支持时，其只能以缴纳碳税来代替减排，即使获得资金支持，制造商也会在减排和碳税缴纳之间进行衡量，决定是否减排。因此，需要从微观层面探讨在工业共生链的减排融资过程中银行、上、下游制造商的行为策略，清晰解释以下问题：政府碳规制政策对上、下游制造商的减排行为有何具体的影响？面临资金约束的上、下游制造商在进行碳资产质押贷款时，银行的贷款意愿受什么影响，其又会对上、下游制造商的减排行为产生何种影响？对于上述问题的研究，在理论层面以及实际运营层面都对工业共生链的形成意义重大。

1 文献回顾

现有文献将工业共生链看作基于工业生态系统（industrial ecosystems）的一种新生产模式［5-6］。从生产流通看，工业共生链是一种特殊的供应链，包含一个上游制造商和一个下游制造商［7］，通过将上游制造商的工业废弃物进行技术处理作为下游制造商的生产原材料，减少资源消耗［8］。近年来，一些学者采用案例研究方法对发达和发展中国家实施工业共生企业群或园区进行总结［9］，实践表明各国的工业共生链条规模与合作类型呈现差异化［10］。例如，丹麦卡伦堡生态工业园，在运行的40年里，证明了产业链条间可资源循环利用，形成了更宏伟的工业共生体系。工业共生链具有经济、环境、社会等多层效益。制造商通过减少原始材料的投入获得了经济效益［11］，同时工业投入使用的原材料和化石燃料数量的减少会使温室气体（GHG）排放量减少［12-15］，带来了环境与社会效益［16］。

供应链中企业减排行为研究主要围绕在政府规制环境下企业减排、如何进行生产等策略选择。①体现在单一环境规制政策影响方面，环境规制的介入有利于共生关系的生成［9，17］。基于DSGE模型，在碳税政策下部门产出和排放与总产出的联动特征遵循传统的顺周期变化模式［18］。当政府实施动态惩罚或补贴措施时，有学者利用演化博弈模型发现“动态碳税”更有利于促进制造商的减排行为［6，19］。在碳配额制度下，针对含有制造商和零售商的二级供应链，有学者利用Stackelberg博弈模型证明了协同合同可以达到减排和帕累托最优情形［20］，联合决策提高了碳减排系数［21］。②体现在组合环境规制影响方面，供应链成员碳减排决策同样受政府碳配额和碳税等混合环境规制政策的影响。单靠碳限额政策无法实现我国减排目标，为使政策发挥最大效力，其应与碳税政策相结合［22］，复合碳政策可在多个层面实现供应链的减排［23］，从效率损失角度来看，与单一政策相比，碳交易和碳税混合政策减排效果更优［24］。③考虑供应链中企业减排技术对资金需求问题。中小企业很难通过传统贷款方式从金融机构等外部融资渠道获得资金支持［25］，因此众多学者围绕如何将碳资产融入融资中展开研究。在碳资产质押贷款的融资模式中，核心企业委托碳资产管理机构做质权人进行碳资产质押融资［26］，进行碳配额质押融资能提高产量增加利润［27］。

基于以上文献分析可以发现：①供应链中企业碳减排行为研究一般将供应链条中的制造商看作一个独立的整体，分析了政府碳规制政策对制造商减排行为的影响，较少考虑工业共生链中各主体之间碳减排的行为差异，实际上工业共生链的主体企业存在着经济效益的合作和社会效益的协同等双重特征；②针对资金约束供应链的融资行为的研究，大都围绕供应链主体以及与银行信用融资对碳减排行为的影响进行分析，缺少针对企业利用碳资产质押融资行为下的减排特征研究，尤其是借助碳资产质押融资对资金约束下的工业共生链碳减排行为的研究缺失。为此，本文在现有文献基础上，将政府作为隐性参与主体，借鉴CAO等［9］和LIU等［28］的研究，引入“动态碳税”的概念，即政府征收的税率随制造商减排比例的变化而变化。在“动态碳税+限额交易”规制政策下，建立银行、上游制造商与下游制造商三方碳减排演化博弈模型，研究碳资产质押融资下的碳减排演化稳定策略。本文重点讨论了银行贷款决策和上、下游制造商减排策略的相互影响，分析了碳税和碳交易价格对工业共生链上、下游制造商减排分别产生的影响，同时也探讨了银行初始贷款意愿以及银行监管成本如何影响上、下游制造商构建稳定的工业共生链。最后，通过数值模拟结果，为政府碳规制政策提供有效的建议，旨在提高工业共生链中的上、下游制造商以及银行的共同利益，推动企业更好地节能减排。

本文的主要贡献体现在以下方面。①从工业共生链的角度，探究具有共生关系的制造商减排行为。将传统供应链中单一制造商拓展为上游制造商和下游制造商，对多个制造商合作减排的行为进行了分析，挖掘了上、下游制造商不同的演化稳定轨迹，以期更好地贴近现实，为共生链中制造商群体的协同减排提供理论支持。②考虑政府组合碳规制政策对具有共生关系的制造商减排行为和银行贷款行为的影响，设计了“动态碳税+限额交易”的环境规制手段，以期为政府碳规制政策的选择提供借鉴，更好地提升环境与经济效益，拓展了工业共生链中碳规制政策的操作空间。③将碳资产质押融入工业共生链中，为工业共生链融资提供了新思路，探讨了银行策略对工业共生链形成作用机理的研究，同时提高了银行、上、下游制造商的共同利益。

2 演化博弈模型的构建

2.1 工业共生链中制造商碳减排融资问题阐述

本文聚焦于工业共生链，考虑了具有潜在共生关系的一个上游制造商和一个下游制造商组成的共生系统。在该系统中，上游制造商可为下游制造商提供异质资源，上游制造商排放的含碳废弃物经过技术处理之后可以作为下游制造商的生产原材料。上、下游制造商关于上游制造商排放碳的处理以及下游制造商生产原材料碳的来源一般分为4种，具体如图1所示。上游制造商生产产生的含碳废弃物经过技术处理后，成为可重新利用的原材料，下游制造商出于其综合利益的考虑，从上游制造商购入含碳废弃物经过技术处理之后的清洁能源，此时减排成本由上游制造商承担，对应图1 中的（a）。上游制造商排放了含碳废弃物，下游制造商获得后对其进行技术处理作为生产材料，此时下游制造商承担减排投入，对应图1 中的（b）。上游制造商在生产过程中产生了含碳废弃物并进行了排放，此时下游制造商直接从供应链外部购入原材料，没有形成含碳废弃物的循环再利用，上游制造商和下游制造商不再形成工业共生链，对应图1 中的（c）。上、下游制造商进行协商共同处理上游制造商产生的含碳废弃物，再将其作为下游制造商的生产原材料，即减排成本由上、下游制造商共同承担，对应图1中的（d）。

图1 工业共生链碳资产质押融资简化流程Fig.1 Simplified flow of pledge financing of industrial symbiotic chain carbon assets

2014年，我国首单碳资产质押贷款项目由兴业银行、湖北碳排放权交易中心与湖北宜化集团签署落地。在单一上游制造商群体和单一下游制造商群体组成的工业共生链中，面临资金约束的上、下游制造商利用碳资产向银行质押融资的流程为［25］：①上、下游制造商分别向碳排放权管理机构（如国家发展和改革委员会）进行免费配额的申请，管理机构为制造商发放碳排放权凭证，形成碳资产；②制造商向碳排放权交易中心（中国7个试点城市）提交碳资产质押业务申请，碳排放权交易中心为制造商出具碳资产所有权等材料。制造商持相关材料向银行申请碳资产质押贷款，并在管理机构办理质押登记；③贷款到期后，制造商按期偿还银行的本息和，银行归还质押的碳资产；④若制造商不能及时归还贷款，则碳排放权管理机构按约定在碳交易市场售卖碳资产偿还银行贷款。

不同于现有文献［20-21］采用Stackelberg博弈模型进行供应链上下游制造商减排行为分析，本文在工业共生链中上下游制造商、银行有限理性假定下构建了演化博弈模型，分析3个参与人如何通过模仿学习找到自己的最优策略。在碳资产质押融资模式中，上、下游制造商利用碳资产凭证向银行质押融资。但因上、下游制造商、银行三者之间信息不对称，道德风险问题时有发生。例如，上、下游制造商获得银行贷款后，综合考虑减排成本、碳税等，可能不开展减排活动从而打破共生关系，不能按期还款。碳排放权交易中心在碳交易市场中出售碳资产，但由于碳资产价格波动，即使碳资产被出售也可能给银行带来损失，因此银行在碳资产质押贷款中存在很大风险性，这是一个三者不断博弈的过程。

2.2 模型基本假设

假设1 本博弈中参与者为上游制造商和下游制造商以及银行三方，且三者均为有限理性且拥有的信息有限，其会根据已获得的信息做出最有利于自身的决策。

假设2 制造商只能在信贷市场上通过银行进行融资。上、下游制造商在未进行减排时资金充足，在进行减排时需从银行贷款，制造商在获得贷款后，其贷款只用作减排，而不作其他用途。

假设3 银行考虑监管成本和上下游制造商按期还款概率，以及上、下游制造商的决策，最终决定是否贷款；上、下游制造商在政府税收、生产成本以及收益等因素影响下选择是否进行减排。银行行为策略集S1＝｛贷款，拒绝贷款｝，上游制造商行为策略集S2＝｛减排，不减排｝，下游制造商行为策略集S3＝｛减排，不减排｝，因而，本博弈共包含了8种纯策略组合。假设各决策主体的决策彼此独立。

假设4 假定上、下游制造商贷款期限为1年，按期还款的比例是一定的，不随经营收益的变化而变化。不管贷款数目如何，银行都需支付一定的监管成本，监管成本固定。

假设5 相比从外界购入原材料，下游制造商使用上游制造商经技术处理后的含碳废弃物作为原材料进行生产的成本更小。

2.3 损益变量选取与测定

具体的相关变量定义参见表1。在碳配额政策下，制造商产量为Qi，单位产品价格为Pi，被赋予一定的碳配额-Li，若碳排放水平LiQi高于-Li，超出限额的部分则需以价格Pc购入。假设对上游制造商产生的含碳废弃物进行技术处理投入为N，当上、下游制造商共同参与减排时，AN和(1- A)N分别为上、下游制造商需承担的减排投入。此时，下游制造商单位成本为Cw，Cw小于下游制造商直接在外部购入原材料的成本C2，下游制造商从上游购入含碳废弃物的单位价格为Pw。制造商可利用碳资产质押向银行借款，假设上、下游制造商按期还款的概率为Si，若制造商不能按时归还贷款，碳资产管理机构在碳交易市场变现Ki比例的碳资产来归还银行贷款，剩余的碳资产归还制造商。若制造商不减排，政府会对其征收碳税，单位碳税为Cti，在动态碳税下，碳税税率随制造商减排比例变化，若制造商参与减排的比例上升，则政府对其征收的碳税税率下降，反之碳税税率增加，从而达到促进制造商自发减排的目的。上游制造商的碳税为(1- y)Ct1，下游制造商的碳税为(1- z)Ct2。假设银行“提供贷款”与“拒绝贷款”的概率分别为x，1-x，x ∈ [0，1]；上游制造商“减排”与“不减排”的概率分别为y，1- y，y ∈ [0，1]；下游制造商“减排”与“不减排”的概率分别为z，1- z，z ∈[0，1]。表2和表3分别给出了银行贷款以及银行拒绝贷款下的上、下游制造商和银行的博弈支付矩阵，其中得益函数的1、2、3列分别代表银行、上游制造商、下游制造商的收益。

表1 上游制造商、下游制造商、银行三方相关变量设定Tab.1 Related variable settings of upstream manufacturers，downstream manufacturers and banks

如表2所示，当上、下游制造商同时参与减排时，二者按比例承担减排成本，此时银行得益函数为上、下游制造商按期还款的收益［ANS1(1+ r) +(1- A)NS2(1+ r)］以及两者不能按期还款时碳资产变现收益造商的得益函数为产品收益（P1Q1）扣除产品成本（C1Q1）以及银行贷款ANS1(1+ r)后与剩余碳资产［Pc(-L1- L1Q1)(1- K1)×(1- S1)］之和；下游制造商得益函数与上游制造商不同之处在于其单位原材料成本为Cw，因为此时下游制造商利用上游制造商排放的含碳废弃物进行生产。在上游制造商参与减排而下游制造商未参与减排时，减排成本由上游制造商承担，下游制造商不再进行贷款，银行得益函数为上游L1Q1)(1- S1)］，最后在此基础上扣除银行监管成本（c）；上游制造商的得益函数与共同参与减排时所不同得将技术处理后的含碳废弃物卖给下游制造商的收益PwL1Q1；下游制造商得益函数同理可得。在上游制造商不参与减排而下游制造商参与减排时，分析原理与上游制造商参与减排而下游制造商不参与减排一样。当上、下游制造商都不参与减排时，银行收益为0，上、下游制造商的得益函数为产品收益扣除生产成本以及碳税后与碳交易收益之和，不过此时碳交易收益为负。

表2 银行贷款下的上、下游制造商以及银行的博弈支付矩阵Tab.2 Game payment matrix of upstream and downstream manufacturers and banks under bank loans

在表3中，因银行拒绝贷款，故银行得益始终为0，即使制造商有减排意愿，在未获资金支持时，其得益依旧为0，而对于不参与减排的制造商，其得益与表2制造商没有减排意愿时的得益是一样的。

表3 银行拒绝贷款下的上、下游制造商以及银行的博弈支付矩阵Tab.3 Game payment matrix of the upstream and downstream manufacturers and banks without bank loans

3 制造商碳减排的博弈均衡性分析

3.1 期望收益函数构建

根据上述碳资产质押融资模型的收益矩阵，构建银行、上游制造商、下游制造商的期望收益函数。

3.1.1 银行的期望收益函数 银行选择贷款和拒绝贷款两种策略的期望效用为Ux和U1-x，由上述表2和表3可计算推导得到

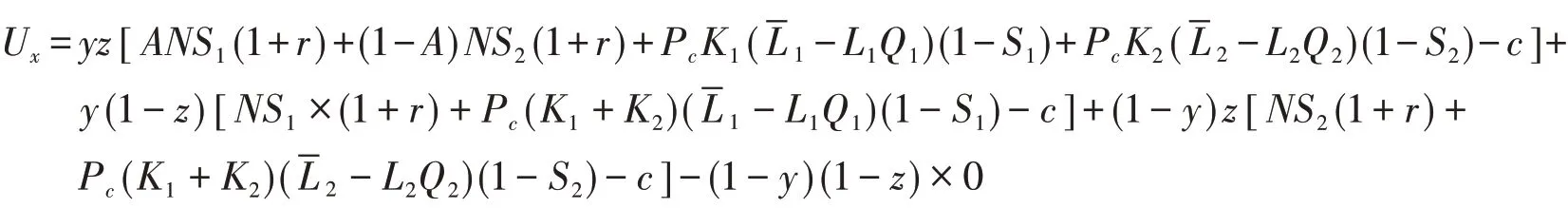
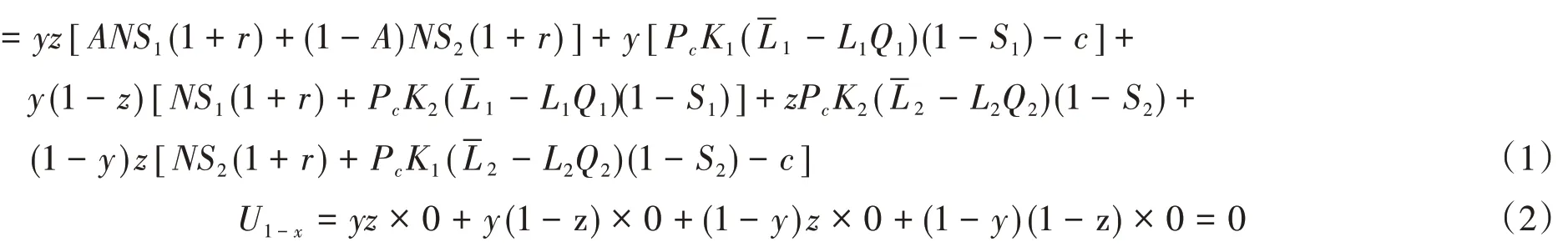
银行的平均期望收益为

3.1.2 上游制造商的期望收益函数 上游制造商减排和不减排两种策略的期望效用为Uy和U1-y，由上述表2和表3可计算推导得到

上游制造商的平均期望收益为

3.1.3 下游制造商的期望收益函数 下游制造商减排和不减排策略的期望效用为Uz和U1-z，由表2 和表3可计算推导得到：

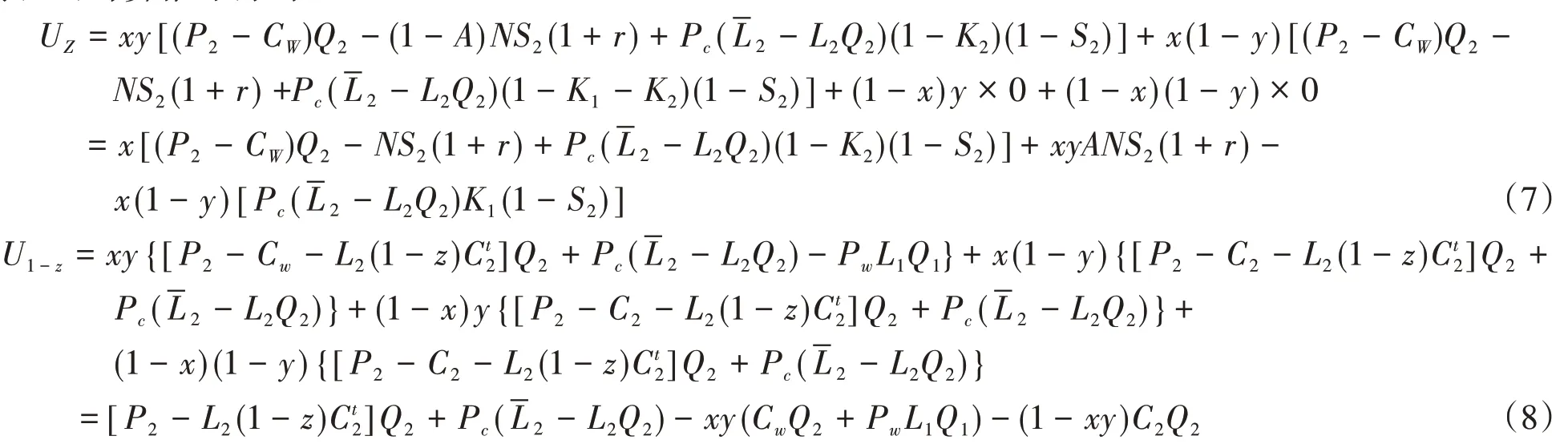
下游制造商的平均期望收益为

3.2 基于复制动态方程的演化均衡策略求解

银行和上、下游制造商三方信息不对称，在博弈过程中，其会根据对方决策不断地调整自己的策略，这就是复制动态方程。在复制动态方程中，如果某个决策给博弈主体带来的收益大于其平均收益，该策略就会被发展。对上述效用函数求微分，由式（1）与式（2）可得银行复制动态方程为

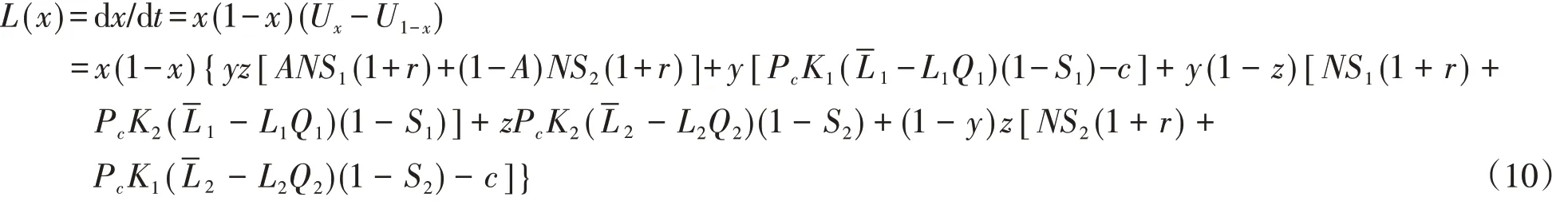
由式（4）与式（5）可得上游制造商复制动态方程为

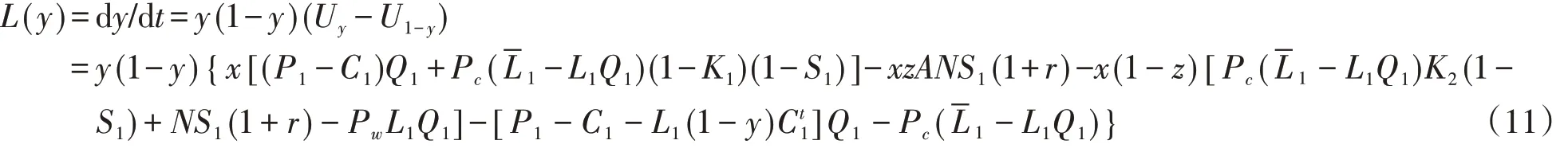
由式（7）与式（8）可得下游制造商复制动态方程为

令复制动态方程式（10）～式（12）3 个方程值dx/dt = 0，dy/dt = 0，dz/dt = 0 得到8 个均衡点，分别为E1(0，0，0)、E2(1，0，0)、E3(0，1，0)、E4(0，0，1)、E5(1，1，0)、E6(1，0，1)、E7(0，1，1)、E8(1，1，1)。 为了找到演化博弈的均衡点，下面对银行和上、下游制造商的演化趋势以及稳定性进行分析。

3.3 均衡点稳定性分析

由式（10）、式（11）和式（12）得到该博弈的雅可比矩阵为J分别求导可判断均衡点的存在性，求导公式如式（13）～式（21）所示。

为了使模型更具有一般意义，假设银行进行贷款的得益大于0；上、下游制造商合作减排的得益要大于制造商不进行减排的收益。按照FRIEDMAN［29］提出的方法，当雅可比矩阵的3个特征值同时为负时，相应的演化点才是演化稳定策略，即ESS；当3个特征值都为正时，所得到的演化点为不稳定点；存在特征值为0时，此演化点为鞍点；当存在正负值时，此情境称为不确定。研究结果如表4所示。

在表4中，存在3个不确定状态，即E5(1，1，0)、E6(1，0，1)和E8(1，1，1)，它们与银行是否选择贷款行为息息相关。当博弈方参数条件发生变化时，这3个不确定状态可以向演化稳定策略转变。因此，本文分别讨论E5(1，1，0)情形、E6(1，0，1)情形、E8(1，1，1)情形下达到稳定点的条件，从而更好地挖掘银行开展贷款行动的影响因素。下面对3种机制下的演化博弈稳定策略分别给出了分析。

3.3.1 E5(1，1，0)情形 当NS1(1+ r) + Pc(K1+ K2)(-L1- L1Q1)(1- S1)＞ c，即银行选择贷款给上游制造商时，其期望收益大于监管成本，因此银行给上游制造商提供贷款。PwL1Q1+ Pc(1- K1- K2)(-L1-L1Q1)(1- S1)-NS1(1+ r) ＞Pc(-L1- L1Q1)，此时上游制造商独自进行减排所带来的含碳废弃物交易收益扣除减排成本后仍大于其不进行减排的碳排放权交易收益，因此其会进行减排。L2Ct2Q2- Pc(-L2-购入的碳排放权之和小于进行减排的得益，故下游制造商选择不进行减排，直接购入上游制造商技术处理之后的含碳废弃物。由表4 可知，E5(1，1，0)所对应的特征值都是负的，在此种情况下(1，1，0)是稳定点，所对应的演化策略为（贷款，减排，不减排）。

表4 各个均衡点的特征值及其正负性Tab.4 Eigenvalue and pm at each of the equilibrium points

3.3.2 E6(1，0，1)情形 当其期望收益大于监管成本，因此银行有意愿给下游制造商贷款。L2Q2)×(1- S2)(K1+ K2)- C2Q2+ NS2(1+ r)，下游制造商独自进行减排的成本小于其采用上游制造商产生的含碳废弃物进行生产的成本，其选择减排ANS1(1+ r)，上游制造商考虑到即使自己不参与减排活动，下游制造商也会独自承担减排责任，因此上游制造商选择不参与到工业共生链中。由表4 可知，E6(1，0，1)所对应的λ 值都是负的，在此种情况下(1，0，1)是稳定点，其所对应的演化策略为（贷款，不减排，减排）。

3.3.3 E8(1，1，1)情形 当S1)＞c，即银行选择贷款给上、下游制造商时，增加的收益大于监管成本，银行有动力贷款给上、下游制造时上游制造商进行减排可获得碳交易收益，在扣除减排成本之后，仍大于其不进行减排的碳交易成本，上游制造商投入资金减排。碳排放权交易收入在扣除购入含碳废弃物所需成本后仍小于其进行减排的得益，下游制造商有减排意愿。基于以上假设和推断，由表4 可知E8(1，1，1)所对应的λ 值都是负值，在此种情况下(1，1，1)是稳定点，其所对应的演化策略为（贷款，减排，减排）。

4 数值实验与仿真

为了更直观地看出政府碳规制政策以及银行决策对于演化稳定性的影响，下面采用MATLAB 进行数据仿真。通过以上分析可知，满足帕累托最优状态的参数条件为

借鉴王垒等［30］在复合碳政策组合对异质性供应链决策影响中的数值设定方法，根据《中国环境统计年鉴》中的工业固体废弃物排放量与治理投资额，并查阅资料获得“国泰安服务中心”中的制造商数量和销售额，将银行初始贷款比例、上游制造商初始减排比例、下游制造商初始减排比例都设定为-0.2。在-此基础上，拟定其他参数数值分别为：Q1= 180，Q2= 60，P1= 1，P2= 1，L1= 0.2，L2= 0.2，L1= 5，L2=5，Pc=0.5，Pw=0.5，N = 6，A= 0.5，Cw=0.1，C1=0.4，C2=0.4，S1=0.75，S2=0.75，r = 0.045，c= 2，K1=0.1，K2=0.1，Ct1=5，Ct1=5，通过MATLAB仿真发现，3个博弈主体均可随着时间推移，全部演化为稳定状态。如图2 所示，给出了上、下游制造商减排的系统演化趋势，通过仿真发现，均衡点最终趋向于(x → 1，y → 1，z → 1)的理想状态，即银行选择贷款，上游制造商和下游制造商均选择减排。在动态碳税下，上游制造商减排意愿与银行贷款意愿成正比，即随着银行贷款意愿的增加，上游制造商减排意愿也在增加。因为银行贷款意愿增加，意味着上游制造商获得减排资金的可能性增加，这将吸引更多的上游制造商参与减排。但是下游制造商减排意愿要大于上游制造商减排意愿，因为下游制造商进行生产的原材料来自于上游制造商技术处理之后的含碳废弃物，与在外界购入原材料相比，其价格要低，因此其进行减排的意愿比上游制造商要更强烈，最终上、下游制造商将形成稳定的工业共生链。

仿真主要分为两部分：①分析政府碳规制政策中碳税、碳交易价格和碳配额对于上、下游制造商减排的影响；②研究银行决策中银行初始贷款意愿和银行监管成本对上、下游制造商减排的影响。

4.1 政府碳规制政策对上下游制造商碳减排行为的影响

政府碳规制政策对博弈均衡的影响主要体现在碳税水平、碳交易价格和碳配额。图3 给出了不同碳税水平下上、下游制造商博弈演化路径。仿真发现，在较高碳税水平时，上游制造商减排意愿增加，而下游制造商的减排意愿下降。不同的碳税水平下，早期上、下游制造商的减排意愿存在较大差异，随着时间的推移，上、下游制造商最终将达到（减排，减排）的稳定状态，形成稳定的工业共生链。

图2 动态演化发展趋势Fig.2 Dynamic evolution development trend

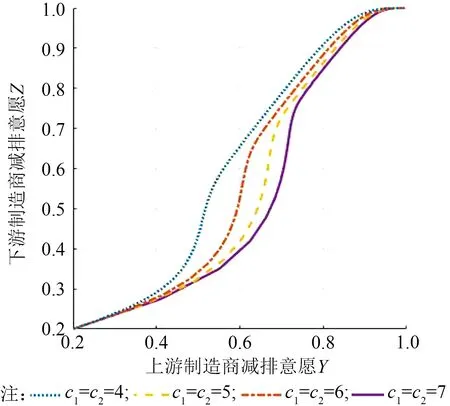
图3 政府碳税变化的演化结果Fig.3 Evolution of government carbon tax changes

从图4可以看出，在不同的碳排放权交易价格下，银行贷款意愿以及上、下游制造商的减排意愿存在着较大差异。当碳交易价格较高时，上、下游制造商更愿意参与减排，而银行贷款意愿会下降。碳交易价格的增长意味着若制造商不进行减排活动，则其购入碳排放权需要支付较大的费用，此时碳排放机会成本极大，因此制造商更愿意参与减排活动，出售自己的碳排放权来获益。

图5给出了政府规定的碳配额I1、I2分别是3、10和20时的不同演化结果，可以看出，随着碳配额的增加，上游制造商和下游制造商的减排意愿均下降，最终稳定的比例也有所减小。因为碳配额的增加意味着制造商碳排放空间的增大，故制造商参与减排的意愿下降，不利于工业共生链的形成。

图4 政府碳交易价格变化的演化结果Fig.4 Evolution of government carbon prices

图5 政府碳配额变化的演化结果Fig.5 Evolution of government carbon quotas

4.2 银行决策对上下游制造商碳减排行为的影响

图6 给出了其他参数不变的情况下，银行初始贷款意愿为0.2、0.5、0.8、1.0时，银行初始贷款意愿对于上、下游制造商减排策略的影响。图7给出了银行不同监管成本对上、下游制造商减排影响的轨迹。

图6 银行初始贷款意愿对减排影响的演化结果Fig.6 Evolution of the impact of banks'initial

图7 不同银行监管成本下的演化发展趋势Fig.7 Evolution of different bank willingness to lend on emissions reduction supervision costs

从图6可以看出，银行初始贷款意愿主要对上下游制造商减排的收敛速度产生影响。随着银行初始贷款意愿的增加，上游制造商减排意愿在减小，而下游制造商的减排意愿在增加，这说明银行贷款意愿的增加抑制了上游制造商的减排意愿，而对下游制造商的减排起到正向作用，这和实践中往往由单一制造商承担减排责任的现象一致。但是随着时间的推移，博弈各方在不断地学习过程中都将演化到稳定状态，最终形成工业共生链。

图7的仿真结果显示，当监管成本在2.8左右时，博弈所得到的均衡结果与监管成本在0.5或2时存在很大的差距，不能达到（贷款、减排、减排）的稳定状态。监管成本的增大会使银行贷款意愿下降，因而制造商的减排活动就会遭遇障碍，上、下游制造商之间不易形成工业共生链。

5 结论和研究展望

5.1 研究结论

在“动态碳税+限额交易”下，本文将政府作为隐性参与主体，考虑了工业共生链中面临资金约束的上、下游制造商，通过建立银行，上、下游制造商三方碳减排演化博弈模型，分析了三方可以达到的演化稳定策略及其所需条件，最后讨论了政府碳规制政策参数和银行相关决策对于演化博弈稳定策略的影响。主要得出以下结论。

在不同的初始条件下，银行以及上、下游制造商可以达到3个不同的稳定状态，即，在这3个稳定点中，银行的最优决策始终是选择贷款给上、下游制造商，而上、下游制造商基于自身利益，存在不减排的可能，也就是说此时的工业共生链是不稳定的。

在“动态碳税+限额交易”政策下，最终银行会贷款给上、下游制造商，上游制造商和下游制造商都将参与减排活动，形成工业共生链。随着碳税水平的提高，上游制造商减排意愿增加，而下游制造商的减排意愿下降，但最终都将达到双方减排的稳定结果，形成工业共生链；碳交易价格越高，上、下游制造商减排意愿越强烈，越有助于形成工业共生链，反之碳交易价格越低，越不利于工业共生链的建成。碳交易价格较高时，上、下游制造商将自发减排，在碳交易市场转卖自己剩余的碳排放权。政府规定的碳配额越高，上、下游制造商参与减排的意愿越低，越不利于工业共生链的形成。

监管成本的增大会使银行贷款意愿下降，因而制造商的减排活动就会遭遇障碍，上、下游制造商之间不易形成工业共生链。银行监管成本的降低对于银行提供贷款意义重大。银行监管成本越低，银行越倾向于向制造商提供贷款。银行贷款意愿的增加抑制了上游制造商的减排意愿，对于下游制造商的减排活动可以起到正向促进作用。但是随着时间的推移，博弈各方在不断学习过程中都将演化到稳定状态，最终形成工业共生链。

5.2 对策建议

在宏观层面，政府可设置有区别的碳税以及碳配额，以调动制造商的减排积极性。对上游制造商可规定较高的碳税，对下游制造商的碳税不宜设置过高。同时，可以适当降低碳配额使更多的上、下游制造商参与减排活动，以形成工业共生链。再者，设置差别碳排放权交易机制。对于高污染行业、高污染区域，政府可规定较高的碳排放权交易价格，并分配其较少的碳配额，以促使其自发参与减排活动，促进工业共生链的形成。

在微观层面，对于上、下游制造商而言，上、下游制造商可设定一个成本分担模型，以达到工业共生链稳定的效果。对于银行而言，为减少监管成本，可以和征信机构合作，建立工业共生链征信体系，对于那些未能及时进行还款的制造商应计入征信档案，在下次进行贷款时要作为重点对象进行考察。同时，对不同的制造商可以有针对性地提出不同的贷款条件，如针对上游制造商可以提出较为严苛的贷款条件，综合考虑上游制造商的经营水平、诚信情况等予以贷款，最终促进上游制造商的减排活动。

5.3 研究展望

本文发现，与政府决策相关的碳税、碳限额等会对工业共生链的形成产生重要影响，然而政府过多的干预可能会导致资源的错配，为了使资源发挥其最大效用，利用市场价格机制可以更好地促进碳交易市场的发展，当前已有“补贴退坡”政策出现。鉴于此，接下来考虑引入政府作为博弈主体，构建政府、上游制造商和下游制造商三方的演化博弈模型，探究“补贴退坡”对工业共生链产生的影响，以期更好地促进工业共生链的形成。