属性值加权的一依赖估测器模型分类算法研究

余良俊,甘胜丰,范正薇

(1.湖北第二师范学院 计算机学院,武汉 430205; 2.湖北广播电视大学 继续教育学院,武汉 430074)

0 概述

分类是机器学习中一项非常重要的任务,是当前人工智能领域的热点研究课题[1]。常见的分类器构造方法有贝叶斯网络、决策树、演化算法、人工神经网络、粗糙集与模糊集等[2]。其中,贝叶斯网络结合统计学、图论的相关知识,成为机器学习领域研究中最为流行的方法之一[3-4],并广泛应用于文本分类[5]、风险预警[6]、核密度估计[7]与情感分析[8]等诸多领域。

为了提升分类性能,研究人员提出了很多贝叶斯网络分类算法,然而学习最优的贝叶斯网络是一个NP-hard问题[9]。朴素贝叶斯网络模型作为贝叶斯网络模型中经典、简单且高效的模型,得到了广泛的研究应用。朴素贝叶斯网络假设属性之间是相互独立的,该假设称为属性条件独立假设。但由于该假设与现实分类问题并不相符,因此影响了朴素贝叶斯网络的分类性能。目前,对朴素贝叶斯网络分类算法的改进研究主要围绕结构扩展[10-11]、属性加权[12-13]、属性选择[14-15]、实例加权[16]以及实例选择[17]等5个方面进行展开,结构扩展方法通过增加有限的有向边来扩展朴素贝叶斯网络的拓扑结构,表达属性变量之间的依赖关系,削弱朴素贝叶斯网络的属性条件独立假设,提升分类性能[18]。

一依赖估测器(One-Dependence Estimator,ODE)是朴素贝叶斯网络结构扩展方法中的经典模型。文献[18]提出平均一依赖估测器(Average One-Dependence Estimator,AODE)算法。在该算法中,类变量作为每个属性节点的父亲节点,同时把一个属性变量作为其余所有属性的父亲节点。TANB(Tree Augmented Naive Bayes)算法[19]以ODE模型为基础,在属性变量之间增加了树结构模型,通过计算属性之间的条件相互信息来确定树结构模型。HNB算法[20]可以避免学习贝叶斯网络拓扑结构,为每个属性节点建模,产生隐性的父亲节点,其是一种特殊的ODE模型结构。

以上算法均可提升ODE模型的分类性能,但查阅最新资料发现,现有的ODE模型分类算法在进行分类判别时,认为不同的属性作为根节点对应的分类器在分类过程中起到的贡献是相同的,然而并未考虑不同的属性作为根节点时对分类过程的贡献不同。因此,本文以ODE模型为基础,采用属性值加权的方法对ODE模型进行改进,利用相互信息(Mutual Information,MI)计算属性值对应的权值,并在标准数据集上对本文提出的MI-ODE算法的分类性能进行评估。

1 算法的建模与设计

朴素贝叶斯网络分类算法作为机器学习领域的经典算法之一,虽然网络拓扑结构简单,但分类效果与其他经典的机器学习分类器模型相当,而且分类性能更稳定、高效,因此得到了研究人员的广泛关注。本文用A1,A2,…,Am表示m个属性变量,待测实例x表示为x=，其中，ai为第i个属性Ai对应的取值。假设属性变量个数为4,朴素贝叶斯网络的模型结构如图1所示。从图1可以看出,朴素贝叶斯网络中属性之间是相互独立的,没有依赖关系。

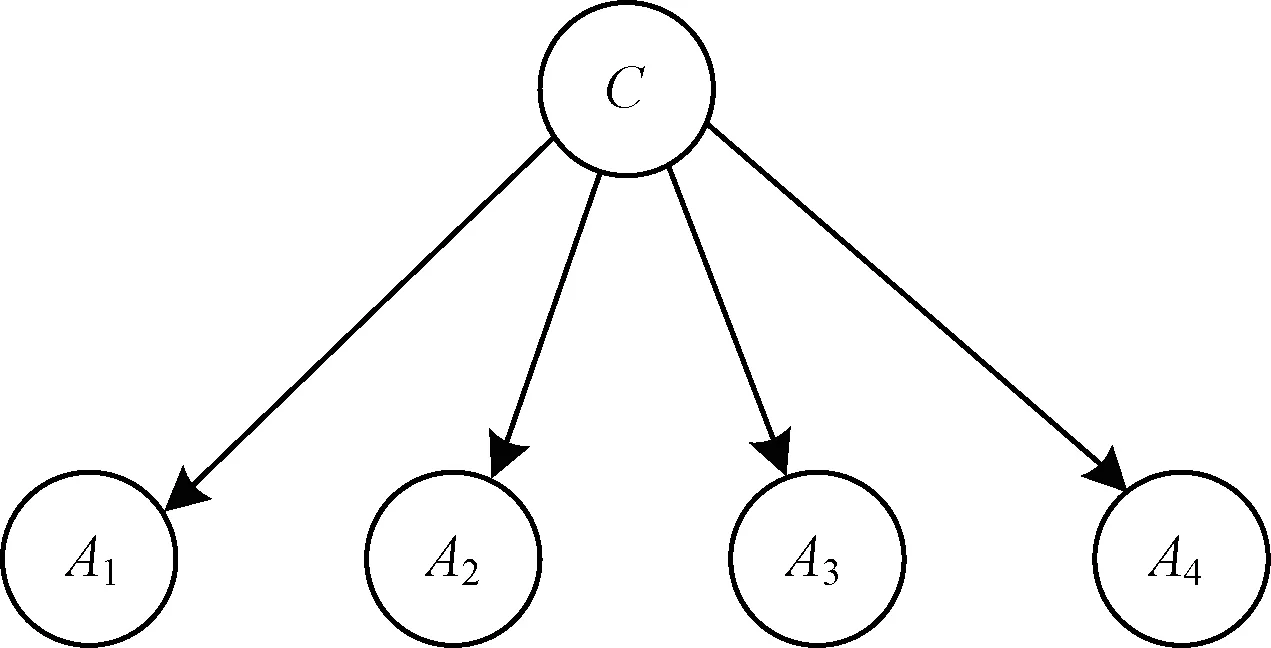
图1 朴素贝叶斯网络模型结构

利用ODE模型对朴素贝叶斯网络的结构模型进行扩展,并对所有的属性都确定一个非类属性的父亲节点,以此来表达属性变量间的依赖关系,提升算法的分类精度。现有的ODE模型分类算法在进行分类判别时,仅对每个ODE模型进行算术平均,并未考虑不同的属性作为根节点时，不同的ODE模型对分类过程的贡献不同。本文将ODE模型与属性值加权方法相结合,以ODE模型为研究基础,开展属性值加权方法研究。在对模型计算权值的过程中,采用MI的度量方式计算属性值父亲节点与类变量节点之间的依赖关系,并作为ODE模型的权值。同时,对ODE分类器模型进行属性值加权平均,并提出MI-ODE算法。本文算法的研究设计分为2个部分:ODE建模和属性值加权方法研究。

1.1 一依赖估测器模型建模

ODE模型在建模过程中,对每一个属性节点构建了一个特殊的树扩展贝叶斯网络拓扑结构,每个拓扑结构就是一个ODE分类器，ODE分类器的个数取决于属性变量的个数。在每个ODE模型中,类变量是所有属性变量的父亲节点。同时，遍历每个属性节点作为父亲节点构建多个树拓扑结构,在每个树结构中每个属性有且仅有一个属性父亲节点。假设属性变量个数为4,AODE模型结构如图2所示。其中,A1、A2、A3、A4表示4个属性变量,C表示类变量,其是每个属性节点的父亲节点。

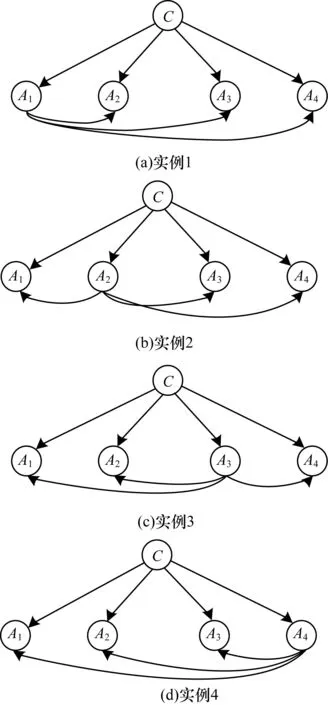
图2 AODE模型结构

在每个ODE模型中,均有一个属性变量是其余所有属性的父亲节点。当属性Ai作为属性父亲节点时,对应的ODE模型分类器用式(1)进行分类:

(1)

其中,ai为第i个属性Ai对应的取值,ak表示父亲节点取值为ai时对应的属性子节点的取值。类标记c对应类变量取值集合C中的某一个取值。概率P(ai,c)和P(ak|ai,c)的计算方法分别如式(2)、式(3)所示:

(2)

(3)

其中,n为训练实例的个数,ai为第i个属性Ai对应的取值,ak表示父亲属性节点取值为ai时对应的属性子节点的取值,ni为第i个属性的取值个数。F(ai,c)表示属性值ai和类标记c同时出现的频率次数,F(ak,ai,c)表示属性值ai、属性值ak和类标记c同时出现的频率次数。当有m个属性变量时,按照图2的建模方式建立m个ODE模型分类器,即对朴素贝叶斯模型进行m种不同的拓扑结构扩展,并根据每个ODE模型分类器计算出待测实例的类标记。

1.2 属性值加权方法研究

MI-ODE算法对ODE模型采取属性值加权方法进行研究,改变了现有算法对每个ODE模型进行算术平均的现状。综合考虑不同属性作为根节点时不同ODE模型对分类过程的不同贡献。本文算法利用相互信息作为信息度量方式,计算属性值父亲节点和类变量之间的依赖关系,对ODE进行属性值加权。对依赖关系大的ODE模型分配大权值,同时给依赖关系小的ODE模型分配小权值。属性值加权的ODE模型结构如图3所示。其中,A1、A2、A3、A4表示4个属性变量,类变量C为每个属性节点的父亲节点，Wi,ai表示第i个属性作为父亲节点,且属性变量的取值为ai时对应ODE模型的权值。

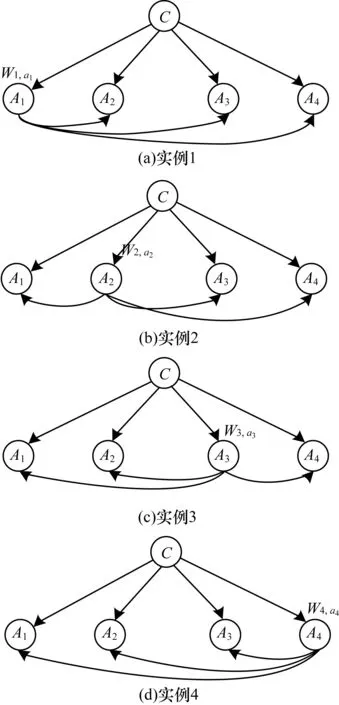
图3 属性值加权的ODE模型结构

MI-ODE算法根据属性变量对ODE模型进行建模,当有m个属性变量时,建立m个不同的ODE模型拓扑结构。但与传统研究方法不同的是,本文MI-ODE算法对每个ODE模型计算了根节点属性值的权值,通过计算属性父亲节点的属性值与类变量之间的关联性来获取ODE模型权重,再对m个不同的ODE模型进行属性值加权平均。

在计算分类精度时,对每个ODE模型引入属性值加权平均,待测实例用式(4)进行分类:

(4)

合理计算ODE模型权重Wi,ai以及合理度量属性父亲节点的属性值与类变量之间的关联性是本文算法的难点问题。MI-ODE算法在计算权重的过程中,采用相互信息作为度量方式来计算某一属性值作为根节点时对应的ODE模型权重。相互信息在信息论中常用来度量2个变量之间的依赖程度,表示2个变量之间的共同信息量[21-22]。属性变量Ai和类变量C之间的相互信息则定义为:

(5)

其中,相互信息MI(Ai;C)度量了属性变量Ai对类变量C的依赖程度,可以反映属性变量Ai在分类过程中的重要性,且其值越大,在分类过程中对应的作用越大。

在本文算法中,需要计算当属性父亲节点Ai取值为ai时,与其对应的ODE模型的权值Wi,ai。Wi,ai表示属性值ai和类变量C之间的依赖关系。根据相互信息度量可得:

(6)

当有m个属性变量时,即可根据式(6)计算出m个不同的ODE模型对应的权值,再根据式(4)对每个ODE模型进行属性值加权平均来求取待测实例的类标记。

本文提出的MI-ODE算法具体步骤为:

输入训练数据集D,测试实例x

输出测试实例x的类标记

步骤1当有m个属性变量时,建立m个不同的ODE模型拓扑结构。

1)对每个属性父亲节点的属性值ai和每个类标记c,根据式(2)计算P(ai,c)。

2)对每个属性父亲节点Ai对应的属性子节点对应的每个属性值ak(k≠i),根据式(3)计算P(ak|ai,c)。

3)对m个不同的ODE模型拓扑结构,根据属性父亲节点的属性值ai,根据式(6)计算对应的ODE模型的权值。

步骤2根据式(4)计算测试实例x的类标记。

步骤3返回测试实例x对应的类标记。

2 实验设计与分析

2.1 实验数据与实验平台

本文研究将借助国际数据挖掘WEKA实验平台以及Eclipse软件进行。实验数据集来源于由加州大学欧文分校经过精心挑选用于现实分类问题的36个UCI标准数据集。数据集来源于现实生活中的分类问题,且包含的实例数众多。不同的数据集包含的实例数和类标记的数量各不相同,因此该数据集在国际数据挖掘领域具有较强的代表性。

由于相关数据挖掘算法只能对名词性属性进行处理,因此首先需要对36个UCI标准数据集进行预处理。本文对数据集的预处理包括采用WEKA实验平台的无导师过滤器Replace Missing Values替换缺失值,有导师过滤器Discretize对数值型数据进行离散,以及无监督过滤器Remove对无用属性进行删除等操作。

2.2 实验设计与结果分析

以预处理后的36个UCI标准数据集为研究对象,借助WEKA实验平台以及Eclipse软件完成实验。实验比较了MI-ODE算法、NB算法、AODE算法以及TAN算法的分类性能。为了更准确地评估本文提出的MI-ODE算法的分类性能,对所有算法均设置了相同的数据集、相同的实验平台以及相同的评估方法,且实验均采用10次十折交叉验证法,并采用置信度为95%的t-test统计测试方法[23]对算法的分类精度以及AUC[24]指标进行分析比较。4种算法的分类精度结果如表1所示,AUC指标结果如表2所示。其中,表1和表2中的w/t/l值是指MI-ODE算法相对于其他算法,在置信度为95%的t-test统计测试方法下得到的比较结果。w表示MI-ODE算法的分类精度高于其他算法的实例集总数量,t表示MI-ODE算法的分类精度与其他算法相等的实例集总数量,l表示MI-ODE算法的分类精度低于其他算法的实例集总数量。

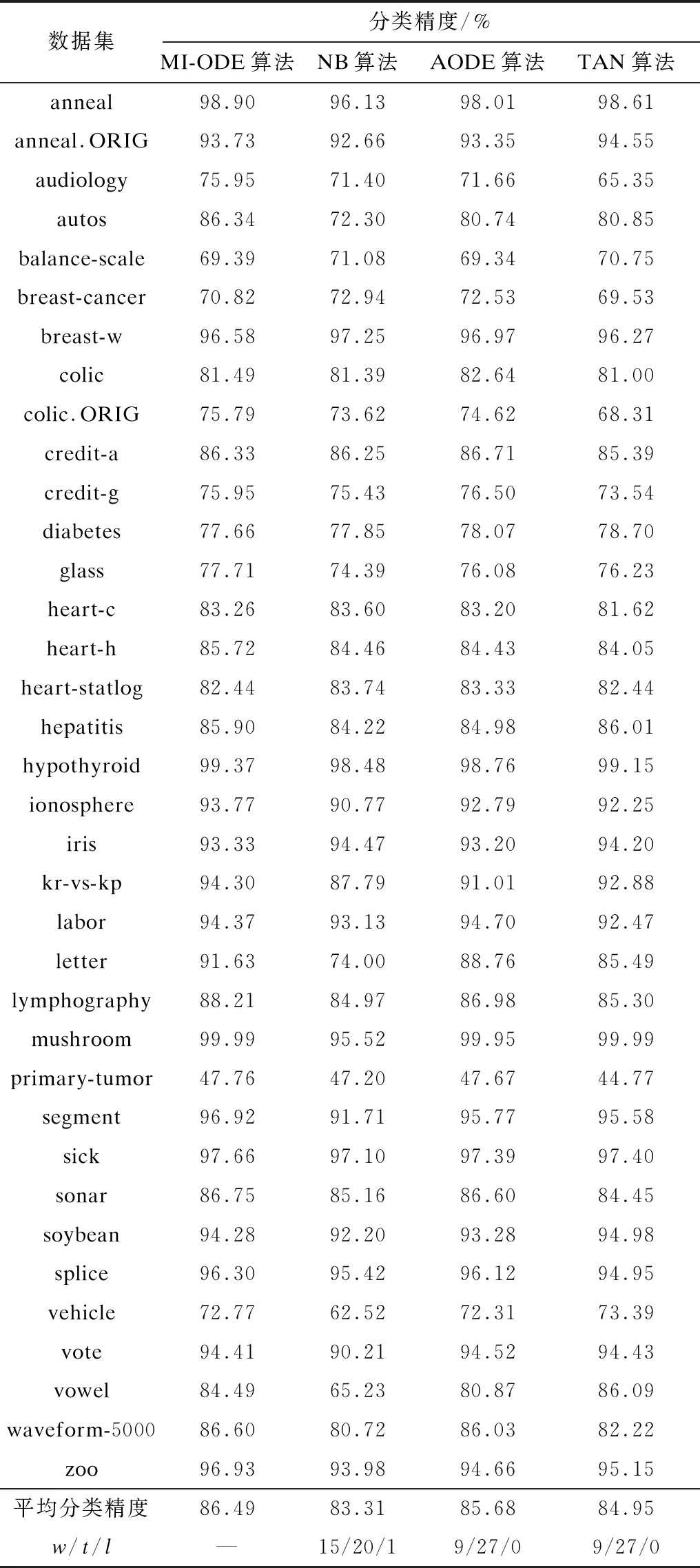
表1 4种算法的分类精度对比

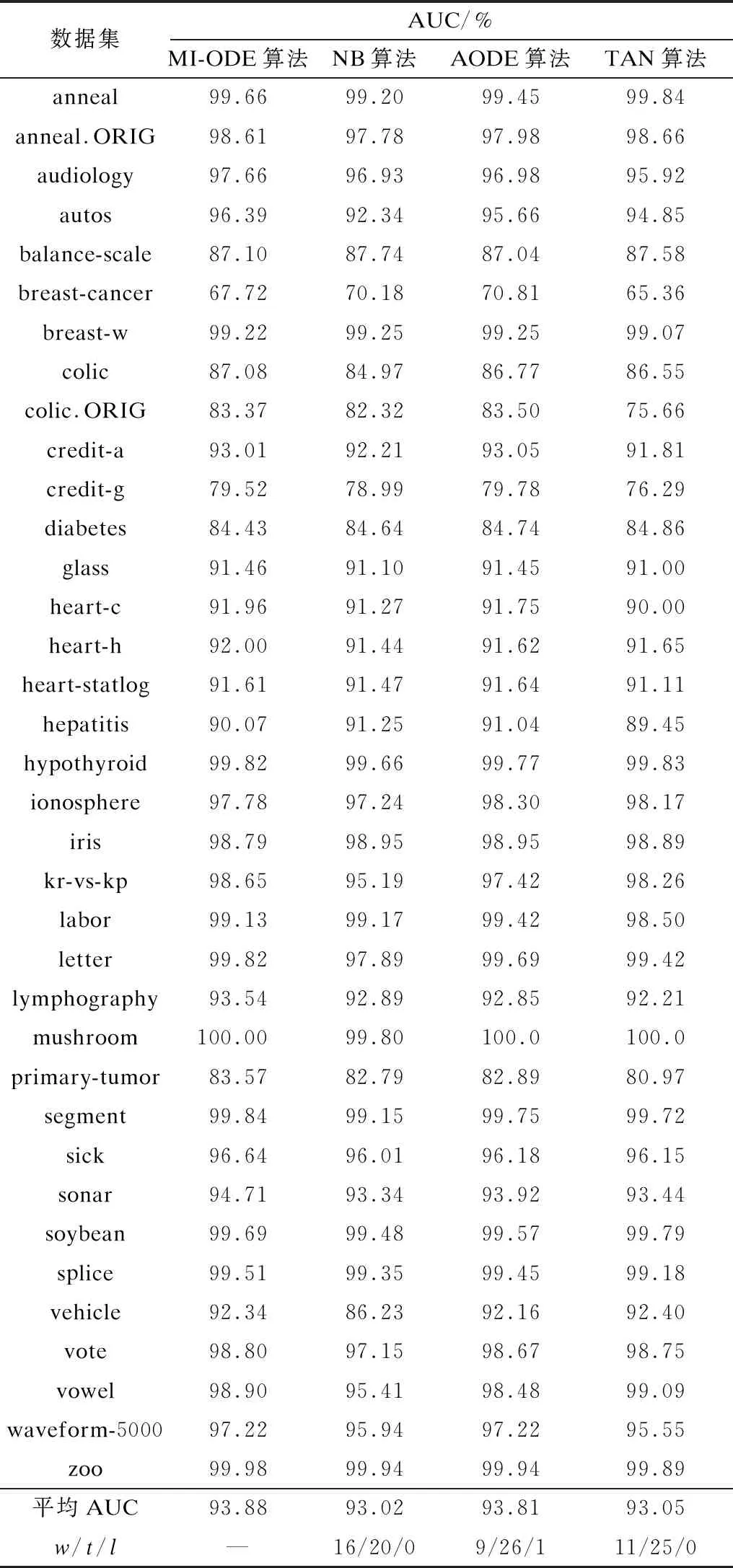
表2 4种算法的AUC对比

从表1可以看出,MI-ODE算法的平均分类精度最高,为86.49%。相较于NB算法,MI-ODE算法在15个数据集上的分类精度有明显提升;相较于AODE算法、TAN算法,MI-ODE算法均在9个数据集上的分类精度有明显提升;相较于NB算法,MI-ODE算法在数据集letter上的分类精度提升了17.63%,提升效果非常显著,这说明相较于其他算法,本文提出的MI-ODE算法的分类精度性能最优。

从表2可以看出,MI-ODE算法的平均AUC指标最高,为93.88%。相较于NB算法,MI-ODE算法在16个数据集上的AUC指标有明显提升;相较于AODE算法,MI-ODE算法在9个数据集上的AUC指标有明显提升;相较于TAN算法,MI-ODE算法在11个数据集上的AUC指标有明显提升;相较于NB算法,MI-ODE算法在数据集vehicle上的AUC指标提升了6.11%,提升效果非常显著,这说明相较于其他算法,本文提出的MI-ODE算法的AUC指标性能最优。

综上所述,相比于NB算法、AODE算法以及TAN算法,本文提出的MI-ODE算法的分类精度和AUC均有所改进,且分类性能最优。

3 结束语

为解决现有ODE模型未考虑到不同属性作为根节点时对分类过程贡献不同的问题,本文提出基于相互信息的属性值加权MI-ODE算法。实验结果表明,MI-ODE算法提升了朴素贝叶斯网络分类算法以及ODE模型经典算法的分类性能。后续将继续以树扩展的朴素贝叶斯模型为基础,对贝叶斯网络分类算法进行改进。