GF-3交叉极化数据的海面风速反演研究

丁 苑,郝明磊,行鸿彦,曾祥能

(1.南京信息工程大学 a.气象灾害预报预警与评估协同创新中心;b.江苏省气象探测与信息处理重点实验室,南京210044; 2.空军研究院 战场环境研究所,北京 100085)

0 概述

海面风场中风速和风向的观测对军事活动和海上生产作业有极其重要的影响,尤其是风速直接影响海上行动的安全。遥感测量海面风速已经成为大尺度风浪观测的重要手段,针对特定远洋海域,其能够弥补传统单点观测数据的缺失。合成孔径雷达(Synthetic Aperture Radar,SAR)对海平面粗糙度的变化十分敏感,且其微波成像方式对云雾穿透性强,受天气状况干扰较小[1],因此广泛应用于海面风速的反演。SAR从其成像中根据不同海面的粗糙度来获取不同的后向散射信号,并按照该信号与风速、风向和雷达入射角之间的数量关系,提取出需要的风场信息[2-3]。SAR按照其发射波束振动方向的不同,可以分成水平极化(H)和垂直极化(V),并按照雷达波束发射-接收的振动方向可分为同极化方式(HH、VV)和交叉极化方式(VH、HV),不同的极化方式接收到的后向散射强度不同,由此对应不同的海面风速反演模型。本文结合以往国际学者的研究,利用逐步回归模型和BP神经网络模型,对我国高分三号(GF-3)交叉极化数据用于海面风速反演进行初步的模型探索。

1 SAR海面风速反演研究进展

目前,研究人员利用地球物理模型函数(Geophysical Model Function,GMF)对海面风速进行反演[4]。经典的C波段单极化GMF模型,最早是由欧洲中长期预报中心(ECMWF)基于遥感卫星ERS-1/2为散射计设计的CMOD系列函数,且该模型后被证实同样适用于C波段VV极化的SAR雷达。CMOD系列函数是一种半经验模型,与SAR雷达后向散射系数、海面风矢量和雷达入射角等参数相关,其经典表达式为:

C(u10,θ)cos 2φ)

(1)

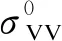
由于经典模型利用单极化SAR图像反演风速必须提前知道相对风向,并将雷达入射角和图像处理后得到的归一化雷达散射截面(Normalized Radar Cross Section,NRCS)作为已知量输入函数模型,通过迭代计算得到海面风速[5],因此选择准确的输入风向非常必要。目前,在海面风场反演研究中,常用的输入风向主要有业务化散射计风向数据、实测浮标数据以及欧洲的风向预报模式,按照不同风速反演精确性的要求选择不同的输入风向[6]。

全极化SAR具备同时获取同极化和交叉极化数据的能力,比单极化SAR数据包含更多的海洋环境信息,特别是交叉极化数据,且其可以获取比同极化数据更丰富的海洋表征信息[7]。随着全球C波段全极化SAR卫星的发射,除了经典单极化模型函数之外,海风反演研究工作者也逐步将研究重心转移到对交叉极化数据(VH、HV)的研究当中[8-9],并研究出一系列新的数据规律。2011年,VACHON等人[10]利用加拿大全极化SAR卫星RADARSAT-2影像,统计出加拿大东西海岸的实测浮标风速,与VH极化的NRCS相结合建立了C-2PO海面风速反演模型:

(2)

该模型认为交叉极化数据的NRCS与海面风速之间是单一的线性关系,且能够降低风场反演模型的复杂程度。随后,文献[11]利用机载步进微波辐射计(SFMR)获取风速数据,并建立了将海面风速与交叉极化NRCS相结合的二次函数模型:

(3)

飓风的研究反演过程认为相对风向对风速反演具有一定的影响力,且随着风速增加相关性不断减弱。文献[12]在C-2PO模型的基础上进一步分析研究,发现交叉极化的NRCS与雷达入射角之间也具有紧密联系,据此提出与风速和入射角相关的C-3PO模型:

(4)

综合上述学者的研究,SAR交叉极化数据运用于海面风场反演的研究表明了相较于经典单极化模型的优越性。但与此同时,运用交叉极化数据反演海面风场的模型仍在学术界未有定论,影响交叉极化反演的因素仍有争论,因此具有进一步研究的价值。

2016年,中国发射了GF-3,该卫星是我国第一颗C波段分辨率为1 m的SAR卫星。GF-3的发射极大推动了我国对SAR的成像观测能力,跻身国际先进行列。由于GF-3正式运行时间尚短,GF-3数据在海面风场反演中的应用研究仍处于起步阶段,准确地对观测海域进行风场反演并验证结果,不仅能推进后续海洋探测,还可以使得我国自主发射收集的SAR卫星数据在军事、国防等领域发挥重要作用[13]。随着机器学习的迅速发展,具有自主学习能力的人工神经网络模型应用于海洋气象领域也获得广泛关注,强大的非线性映射能力使其对复杂应用问题具有良好的适应性。本文选用80幅GF-3全极化条带1(QPSI)的交叉极化(VH)数据,分析风速、相对风向及雷达入射角等各因素与提取的NRCS之间的关系,随后分别利用逐步回归模型和BP神经网络模型进一步研究各变量之间的相关关系,初步探索我国GF-3交叉极化数据的风速反演模型。

2 数据预处理

2.1 SAR数据及其预处理

GF-3具有全极化条带、精细条带、波模式等12种成像模式[14],其空间分辨率为1 m～500 m不等,幅宽为10 km～650 km,常规入射角为20°～50°。本文研究选择的是全极化条带1(QPSI)模式,该模式下的产品是单视复数据,SAR图像标准空间分辨率为8 m,标准成像幅宽为30 km。

原始SAR图像数据存在相干斑噪声、几何畸变等问题不能直接用于风速反演,需要进行图像预处理。首先,预处理操作是辐射定标,即将像元灰度值按照一定的标准转换成以dB为单位的雷达后向散射系数,从而建立目标NRCS与雷达影像强度的定量模型关系。本文利用PIE对GF-3数据进行逐个像元的辐射定标。其次,由于SAR影像的斜视成像机理,为了获取其正确空间地理位置信息,需要对图像进行必要的几何校正[15],使其转换到统一的地理坐标系中,具体如图1所示。由于本文研究的是远离陆地的海洋区域,海面相对陆地起伏较为平缓,可忽略叠掩等造成的几何畸变,因此本文采用WGS84地心坐标系对图像进行椭球体编码。

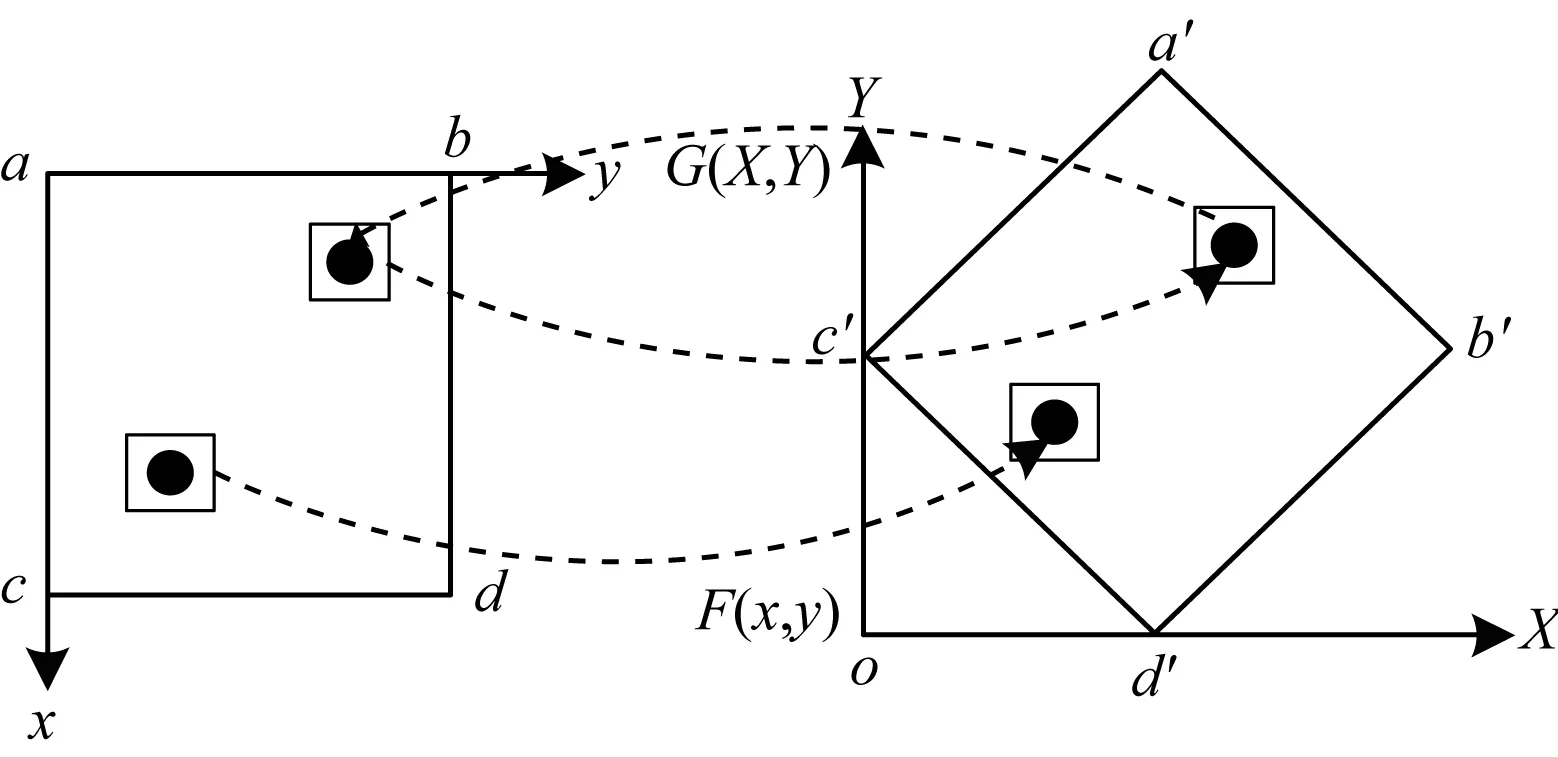
图1 地理编码示意图

为了有效抑制SAR图像中普遍存在的斑点噪声,对图像进行滤波处理是有效剔除噪声的方法,基于完全的斑点乘性噪声模型提出Lee滤波[16],它是经典的SAR图像斑点噪声滤波方法,但其对于图像边缘等细节信息方面的保持不理想,因此本文选用改进的增强型Lee滤波,可以在减少斑点噪声的同时,兼顾保持雷达图像的纹理信息,其滤波效果如图2所示。

图2 改进的Lee滤波效果

2.2 ECMWF海面风场数据

ERA-Interim海面风场资料是由欧洲中期天气预报中心(ECMWF)提供的覆盖全球区域的大气分析产品。该产品提供全球1979年1月至2019年3月的海面10 m高的水平(U)、垂直(V)风矢量分量,根据分量计算得出相应风速、风向,后续数据仍在持续更新中,覆盖全球0°E～360°E、90°S～90°N[17],且有多种空间分辨率选择范围,本文选择最精细的0.125°×0.125°分辨率以使得在空间上与GF-3图像最匹配。在ERA-Interim产品的时间分布上,分为分析数据(Analaysis)和预报数据(Forecast)。对于分析数据,其时间分辨率为6 h(00:00,06:00,12:00,18:00)。在每日00:00与12:00时提供预报数据,用户可根据需求选择预测时间步长,如图3所示。本文为更准确地验证反演结果,在时间数据选取上按照实测优于预测、与SAR图像采集时间最近为原则选取模式资料。

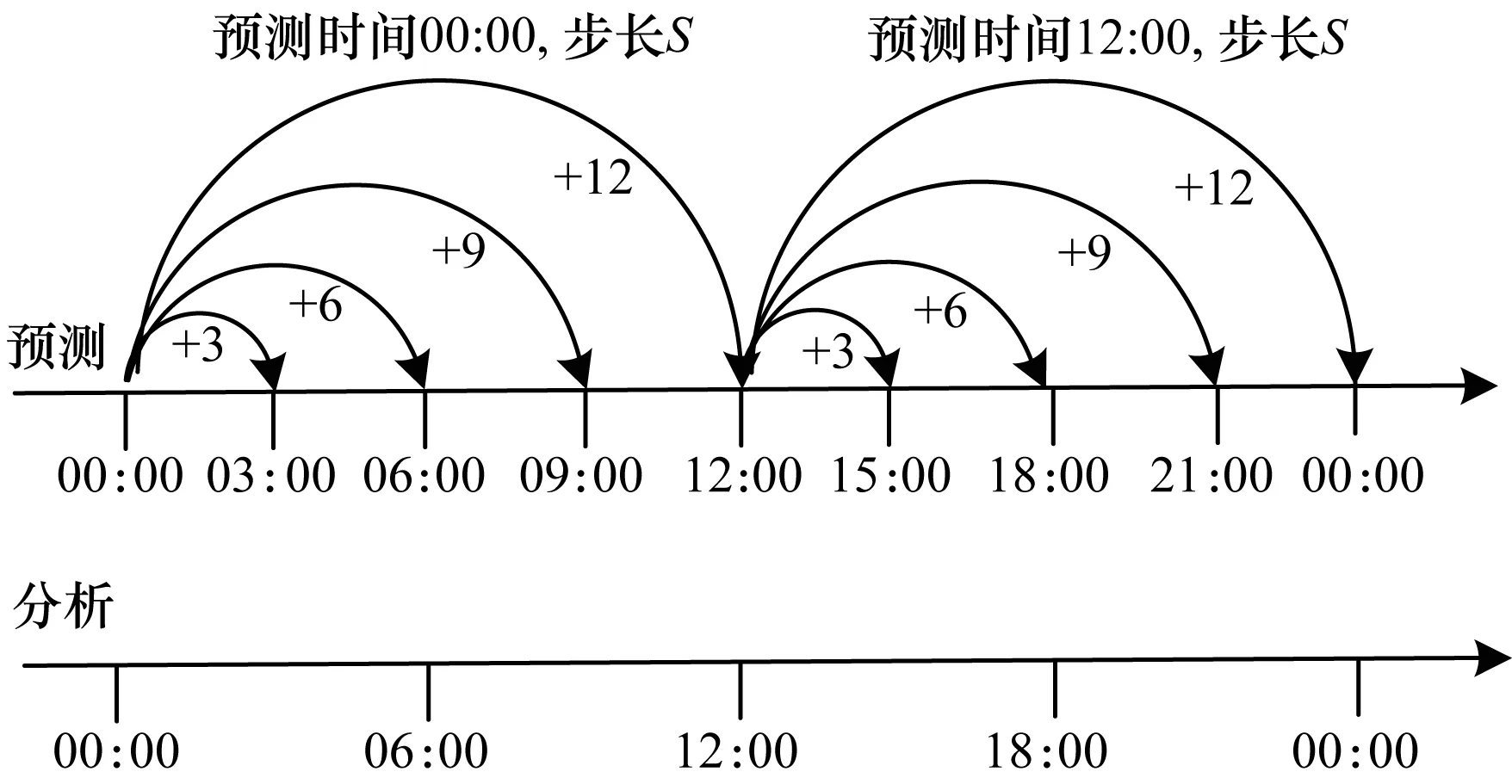
图3 ERA-Interim数据时间分布

3 逐步回归模型建立

3.1 相关性分析

为了更准确地建立多变量回归模型,在回归之前首先对各变量之间的相关性进行分析。根据单极化业务GMF模型的各变量关系,参考以往研究学者对RADARSAT-2交叉极化数据建立的C-2PO模型,本文对VH雷达后向散射系数(σVH)、10 m高风速(u10)、相对风向(φ)、雷达入射角(θ)4个变量之间的线性相关性进行分析。

皮尔逊相关系数是用来描述2个变量之间线性相关性的系数,其取值反应了两者的线性相关程度。该系数定义为2个变量的协方差除以标准差,具体表示方法为:

(5)

式(5)定义了总体相关系数,为进一步计算出协方差和标准差,常用r表示皮尔逊相关系数:

(6)

皮尔逊相关系数r的取值范围为-1≤r≤1,r>0时表示正相关,r<0时表示负相关,|r|=0表示不存在线性相关,|r|=1表示完全线性相关,0<|r|<1表示存在不同程度的线性关系,且|r|≤0.3表示不存在线性相关,0.3<|r|≤0.5表示为低度线性相关,|r|>0.5表示为显著线性相关。

利用上述关系求解得到本文各变量之间的皮尔逊相关系数,如表1所示。根据各变量之间的相关性,可初步判断方程的因变量与自变量之间的线性关系,排除多重共线性干扰,为回归模型的建立提供判断依据。

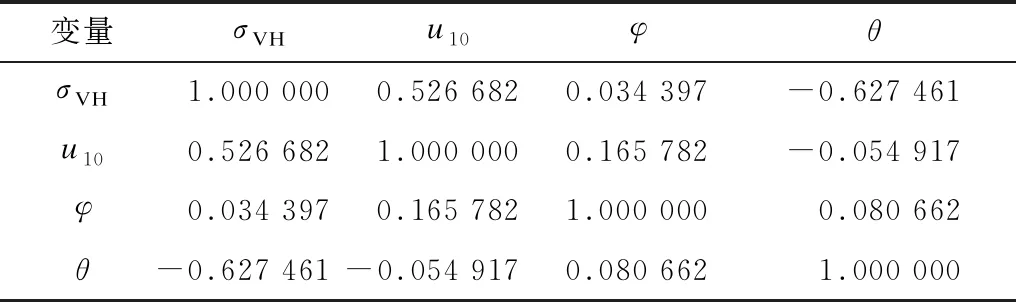
表1 各变量间的皮尔逊相关系数

由表1可知,在GF-3交叉极化数据中,雷达后向散射系数与风速呈显著线性正相关关系、与雷达入射角呈显著线性负相关关系,且其余各变量之间不存在线性关系。

3.2 多元逐步回归分析

多元逐步回归分析是用于研究因变量y与p个因子x之间的定量统计关系,其基本应用原理是对全部自变量按照其对因变量的显著性从大到小逐个引入回归方程。与此同时,对每一个代入的自变量逐个进行F检验,同时,对所有已经引入的自变量进行t检验。如果当前回归方程由于引进了新的自变量而变得不显著,则剔除该变量[18]。逐步回归方程形式如下:

y=β0+β1x1+β2x2+…+βpxp

(7)

基于以上变量之间的相关性分析,将雷达后向散射系数(σVH)作为因变量,逐个引入风速(u10)、相对风向(φ)、雷达入射角(θ)可作为自变量因子,根据引入新变量后回归方程的可决系数、t检验、F检验,若检验都通过则引入,否则剔除。逐步回归后,得到如表2的预测回归结果。

表2 逐步回归结果

由数据分析结果可知,在逐步回归过程中,相对风向φ变量被剔除,F检验与t检验均能拒绝原假设,排除了变量间的多重共线性,与相关性分析结果具有较好的一致性。因此,最终交叉极化雷达后向散射系数的最优多元逐步回归方程为:

σVH=0.343u10-0.227θ-16.502

(8)

根据最终得到的回归方程,风速反演方程可表示为:

(9)

4 BP神经网络的训练与预测

在逐步回归的线性模型中,排除了相对风向因子,但非线性并不意味着无关性,不能直接排除相对风向因子对风速反演的贡献。在已知风速反演与雷达后向散射系数、雷达入射角相关的情况下,进而探究相对风向作为非线性因子对风速反演的影响。当工程中遇到复杂的非线性系统,系统状态方程复杂或无法用数学方法直接建模时,可建立人工神经网络模型表达这种系统[19],即“黑盒”处理。BP神经网络的拓扑结构如图4所示。

BP神经网络是一种带有隐含层的前馈神经网络,其将信号通过输入层输入网络,随后经过中间的隐含层逐层训练计算,再到输出层输出结果,这是网络的前向传递,每一层的计算结果只影响与其关联的下一层神经网络状态[19]。如果输出的结果不是预期结果,网络会进入反向传播计算,按照误差计算规则改变网络权值的阈值,重复整个过程直至得到期望输出结果。本文选用经典的三层BP神经网络建立2个风速预测模型,第一模型是参考前文的逐步回归模型,建立以σVH与θ为输入、u10为输出训练的神经网络预测模型,并将该80组数据作为训练样本,通过BP神经网络的自适应能力预测海面风速。第二模型是在原基础输入层上加入φ,随后将2种模型的训练效果进行对比,侧面判断风向φ是否影响海面风速的预测,BP神经网络模型如图5所示。

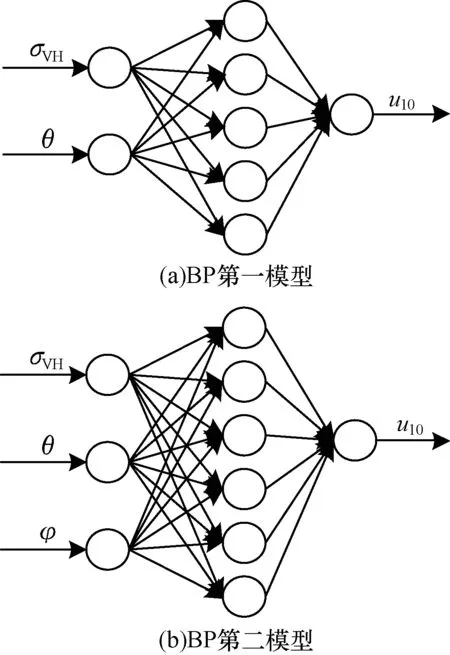
图5 BP神经网络模型拓扑

从BP神经网络模型拓扑可以明显看出,BP神经网络在数学上表达的是一种函数的非线性映射关系。其中,隐含层神经元个数的设定通常有如下公式[20-21]:

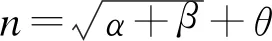
(10)

其中,n为隐含层的神经元数目,α为输入层神经元数目,β是输出层数目,θ是整数,取值区间为[1,10]。基于此,2个模型隐含层神经元个数分别设为5与6。本文的激活函数选择Sigmoid函数,训练中选择基于梯度下降法的Learngdm算法作为权阈值的学习法则,设置最大训练迭代次数为1 000次。BP神经网络模型流程如图6所示。

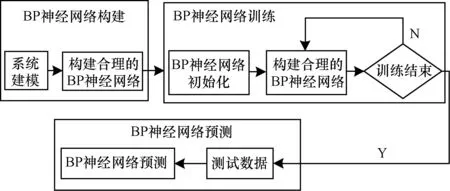
图6 BP神经网络模型流程

2种模型的训练结果如图7、图8所示。从图7可以看出,2种BP神经网络模型的训练数据、验证数据、测试数据的均方误差都迅速减小并最终收敛,所有集合数据对应的拟合R值均超过70%,说明建立BP神经网络预测海面风速是有效的。同时,通过第一模型与第二模型训练效果的对比可看出,相对风向的加入并没有使得模型的训练效果得到显著提升,从而运用排除法基本排除交叉极化数据中风向因素对风速反演的影响。

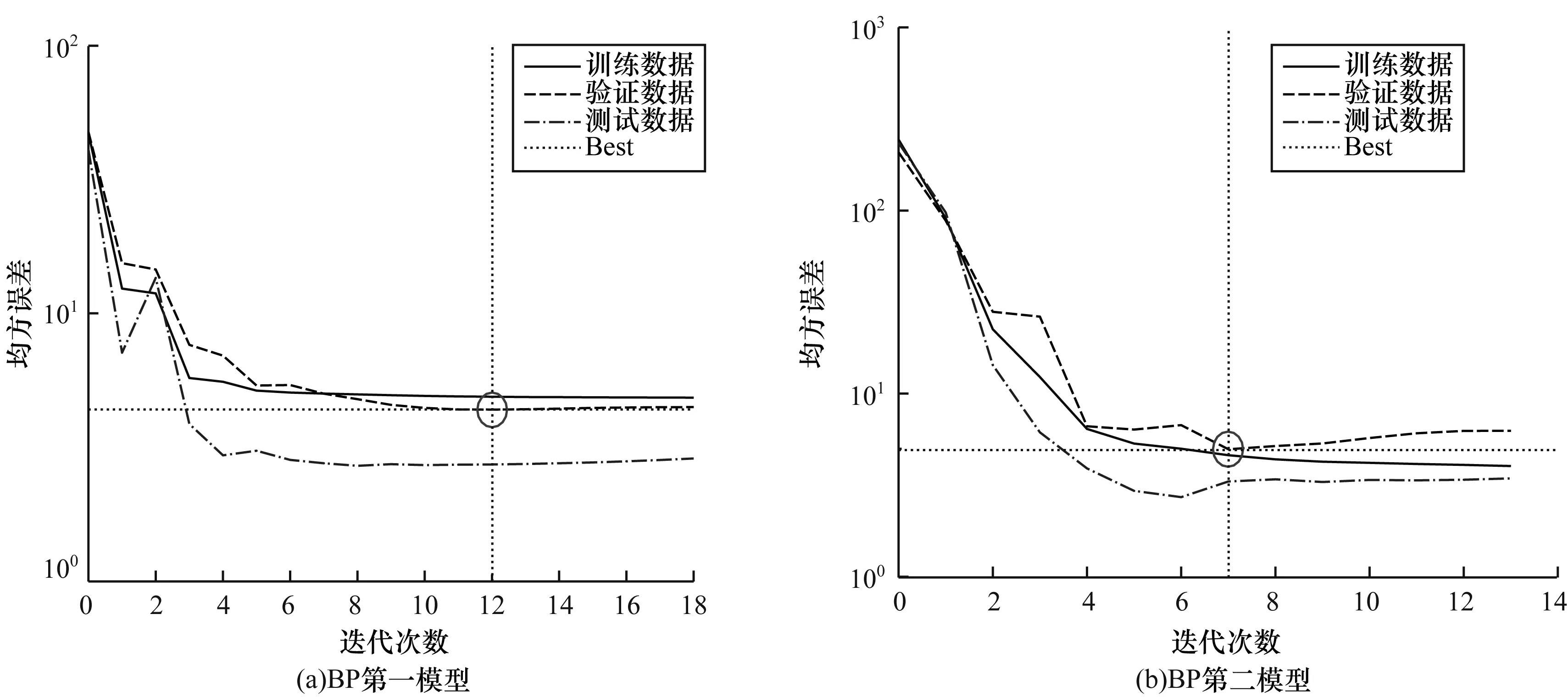
图7 迭代训练结果

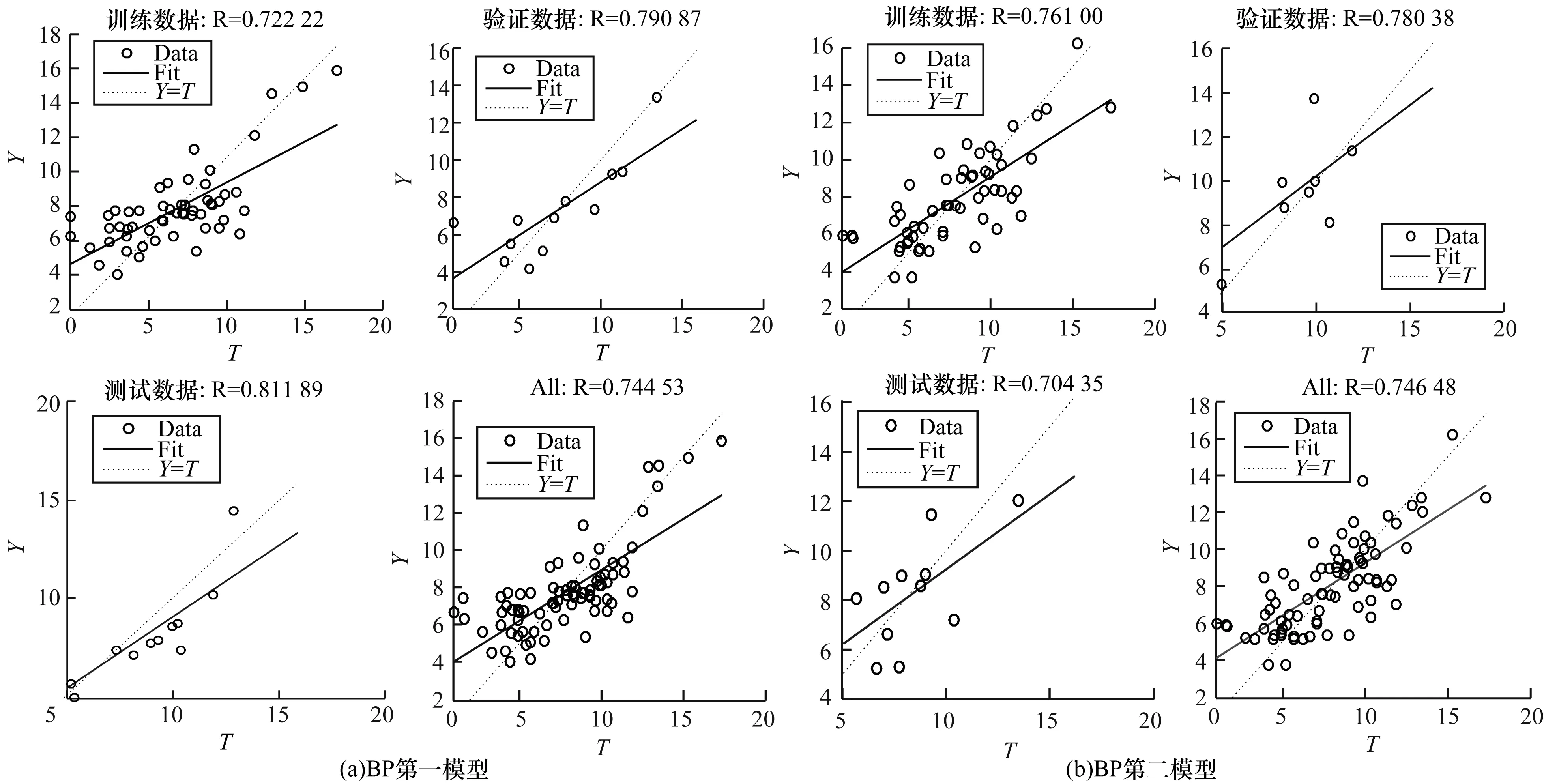
图8 2种BP神经网络模型的训练效果

5 模型评价与结果分析

为评价建立的逐步回归模型与BP神经网络预测模型对海面风速的计算效果,本文另取10幅相同模式GF-3图像作为测试组数据,分别采用逐步回归模型、BP第一模型、BP第二模型和C-3PO模型对海面风速进行反演和验证。模型以ERA-Interim的风场数据作为初始风向与风速验证数据,4种模型对测试组SAR图像数据的风速反演相对误差与风速反演效果分别如图9、图10所示。为更好地体现新模型探究和建立的必要性，本文从宏观数据源到测试样本误差进行了对比与分析。以ERA-Interim的风场数据作为初始风向与风速验证数据，用测试数据组的平均相对误差(Average Relative Error，ARE)以及样本的均方根误差(Root Mean Square Error，RMSE)作为评价标准，结果如表3所示。

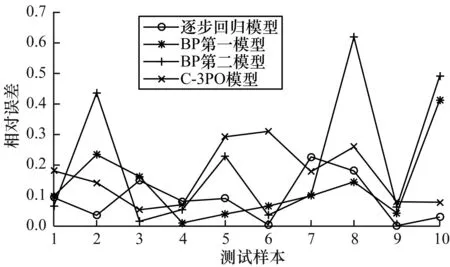
图9 4种模型对SAR图像数据的风速反演相对误差

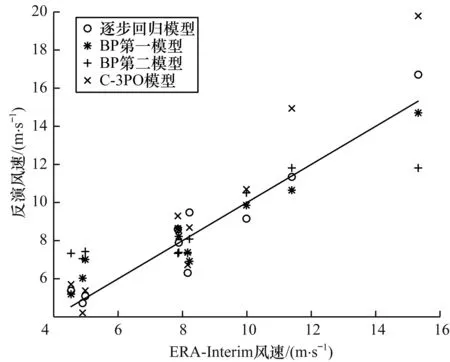
图10 4种模型对SAR图像数据的风速反演效果

表3 4种模型的实验结果对比

结果表明,当前关于交叉极化数据反演海面风速的模型,在数据源上使用的主要是国外卫星,在初始风场数据选择上,C-3PO模型对大量NDBC浮标实测数据进行统计,而我国自主发射的GF-3运行时间尚短且成像区域能够匹配的NDBC数据很少,该模型不能完全适应我国GF-3卫星数据,因此探索建立新模型非常必要,测试数据误差对比也说明了这一点。本文建立的逐步回归模型对测试样本的平均相对误差最小,而BP神经网络预测模型的均方根误差最小,同时,4种模型对GF-3图像交叉极化数据的海面风速反演均方根误差均小于2 m/s,说明模型的建立是显著有效的。与此同时,BP第二模型在训练效果与测试样本误差分析中的效果均未超过第一模型,这些对比排除了风向因子对交叉极化数据雷达后向散射系数的影响,反映了BP神经网络能够较好地模拟风速影响模型,对风速预测的训练具有较强的自学习能力。

6 结束语

本文利用80幅GF-3全极化图像对GF-3交叉极化数据进行海面风速反演,并初步探索了回归方程。实验结果表明,交叉极化数据的雷达后向散射系数与海面风速、雷达入射角之间存在线性关系,与国际学者的研究具有良好的一致性。同时,将BP神经网络引入交叉极化数据对海面风速的反演,一方面说明了神经网络模型在该领域的良好适用性,为未来将更多的人工智能技术运用于海面风场反演提供可能性。另一方面通过2种BP神经网络模型的对比排除了相对风向对海面风速反演的影响,使得风速反演不需要依赖于外部风向的输入,极大简化了反演模型,证明了使用交叉极化数据进行海面风场反演具有单极化数据不可替代的优越性和发展潜力。随着高分三号卫星的继续运行和各幅图像的等效噪声校准,能够得到更显著的数据规律和更精准的反演模型。后续将利用遗传算法来优化BP神经网络，进一步研究机器学习与深度学习在SAR图像海面风场反演领域中的应用。