基于Fluent的金属硬密封球阀流场数值模拟

李 力 何世权 王佳琪 张 锦

（南京工业大学机械与动力工程学院）

阀门作为管道系统中的重要组成部分，具有截止、调节、导流、稳固及分流等功能，因此阀门的工作性能直接影响着整个管道系统的性能［1，2］。球阀作为最常用的阀门之一，多年来一直是国内外学者研究的重点［3～6］。

随着计算机和计算流体力学的不断发展，采用有限元分析方法对球阀的研究日益深入［7～9］。金属硬密封球阀广泛应用于石油、煤化工、电力及冶金等行业，笔者针对NPS8、Class900金属硬密封球阀进行数值模拟，分析球阀内部流场的流动状态， 并对比分析流量系数理论值与模拟值曲线，对球阀的结构设计和优化提供一定的参考。

1 数学模型

1.1 质量守恒方程

单位时间内流入的质量流量等于单位时间内流出的质量流量，称为质量守恒方程或连续性方程。 其微分表达式如下：

式中 t——时间；

u、v、w——x、y、z方向上的速度分量；

ρ——流体密度。

对于不可压缩流体，其密度为常数，则式（1）可简化为：

1.2 动量守恒方程

流体运动过程中，流体动量对时间的变化率等于外界对之作用的各种力的和，称为动量守恒方程或纳维-斯托克斯方程。 其微分表达式如下：

式中 fx、fy、fz——控制体质量力的分量；

p——流场控制体上的压力；

∂τx、∂τy、∂τz——流场控制体表面受到的粘性应力τ的分量。

1.3 标准k-ε湍流模型

标准k-ε湍流模型是一种高雷诺数的模型，其运输方程如下：

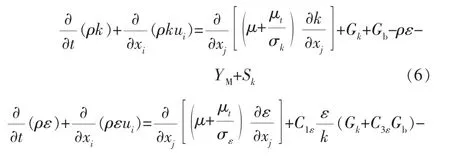
2 球阀的理论流量系数计算

2.1 流场条件的假设

球阀的转动角度是指阀门从全开到全关过程中所转动的角度； 通过介质为25℃的不可压缩的常温水；介质沿着通道x方向径向流动，其他方向的速度矢量都为零。

2.2 介质流动状态的判定

介质的流动状态通过雷诺数Re来确定，Re=VD/γ，其中流道直径D=0.202m，流动速度V=1m/s，流体运动粘度γ=1×10-6m2/s， 经计算，Re=2.02×105＞4000，故管道内流动状态为湍流。

2.3 球阀的阻力系数

阻力系数K是代表阀门流阻的无量纲数，它的大小取决于阀门产品的尺寸、结构、内腔形状及材料粗糙度等。 将阀门流道划分为多段，对各个段落的流道分别计算出各段阻力系数，最终可得阻力系数K：

式中 km——各段阻力系数。

球阀阻力系数由沿程阻力系数k1、 流道起始段与末段阻力系数k2和开度阻力系数k3组成。

对于有压流的圆管，沿程水头损失hf为：

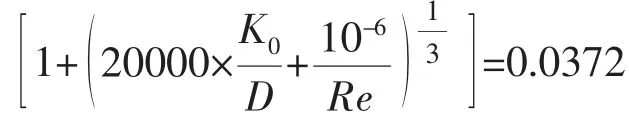
球阀的开度阻力系数k3见表1。

表1 球阀的开度阻力系数k3

把k1、k2和k3带入式（8），可得到球阀不同转动 角度下的阻力系数K（表2）。

表2 球阀不同转动角度下的阻力系数K

2.4 球阀的流量系数

阀门流量系数是流体流经阀门产生单位压力损失时流体的体积流量或质量流量。 在实际工程计算中，常用μ、μF表示阀门流量系数，阀门流量系数的经验公式为：

其中，当流道半径R=0.101m时，流道截面积F=πR2=3.14×0.1012=0.032m2。

把表2中球阀不同转动角度下的阻力系数K带入式（10）、（11），得到球阀不同转动角度下流量系数μ、μF的理论值（表3）。

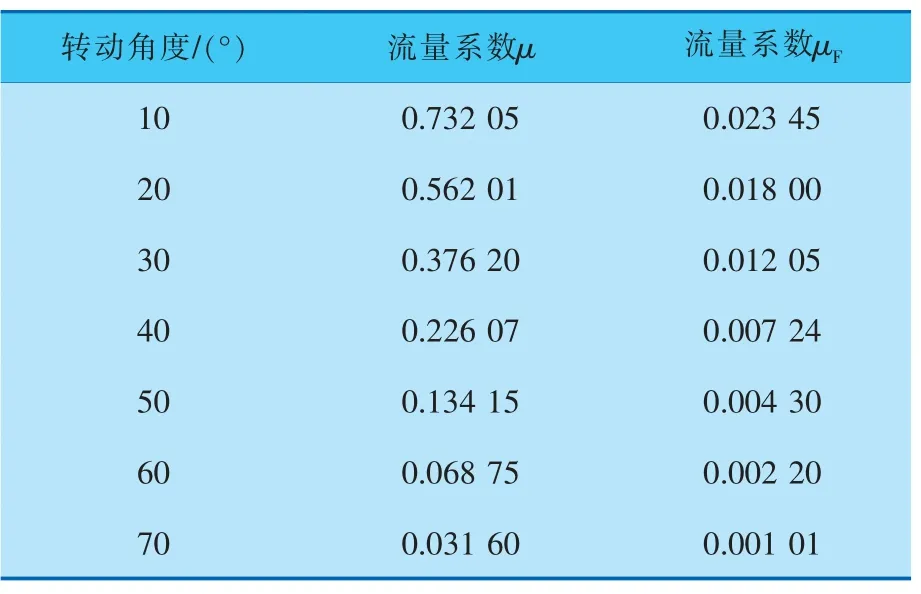
表3 球阀不同转动角度下流量系数μ、μF的理论值

2.5 球阀的压差

流体流经阀门时，流体阻力损失以阀门前后的流体压差表示。 压差Δp的计算公式：

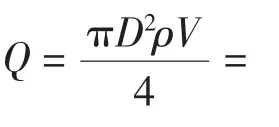
计算得出球阀不同转动角度下的压差理论值（表4）。

表4 球阀不同转动角度下的压差理论值

3 三维建模及网格划分

3.1 几何模型

笔者对NPS8、Class900金属硬密封球阀进行流场分析， 采用SolidWorks进行装配体的三维建模，如图1所示。 在保证球阀主要特征和计算精度的前提下，对球阀微小尺寸作适当简化。 为贴近实际工作情况、提高计算精度，在阀门前后两端各添加5D和10D长度的管道。

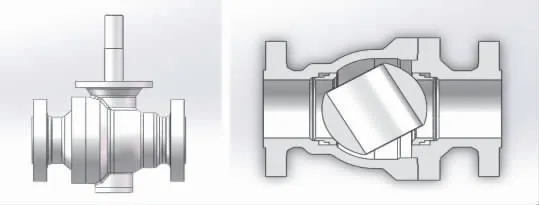
图1 球阀的三维模型

3.2 网格划分

采用DesignModeler软件抽取球阀不同开度下的流道，并利用slice功能对流道进行切片，流道划分为阀前部分、中间部分、阀后部分。在ANSYS Fluent的Mesh平台中， 对流道进行网格划分。 阀前、阀后部分采用六面体网格划分，body size设为6.0mm。 阀门中腔部分body size设为4.5mm，并对阀座与球体交接区域、阀座与阀体交接区域进行网格加密处理。 球阀转动30°的流道网格如图2所示，网格数约为1 082 195。

图2 球阀转动30°时流道网格

4 数值模拟

4.1 边界条件设置

流体为常温水，采用标准k-ε湍流模型及标准壁面函数，根据设计工况给定入口边界条件为速度入口，速度为1m/s，出口边界条件为压力出口，出口压力为10MPa，湍流强度设为5，水力直径设为202mm。 采用基于单元的格林-高斯的SIMPLE算法，求解精度设为二阶迎风。

4.2 结果分析

图3为球阀在不同转动角度下的xz截面压力云图。 当阀门转动角度较小时，阀门处于大开度情况，阀门前后压差较小，流动较稳定。 随着阀门转动角度的增大，阀门开度逐渐变小，阀前形成高压区域，阀门前后压差大幅增大，介质的能量损失也大幅增大。

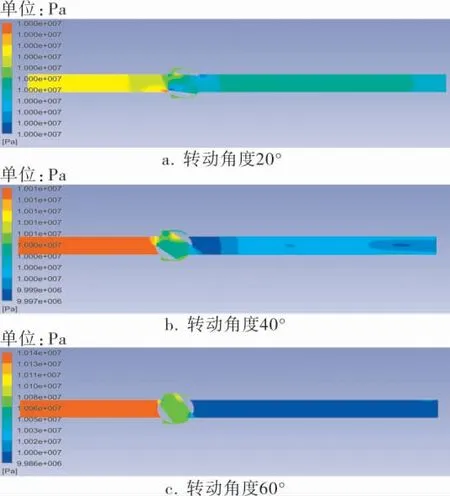
图3 球阀在不同转动角度下的xz截面压力云图

图4为球阀在不同转动角度下的xz截面速度云图。 当阀门转动角度较小时，流场的高速流动区域贯穿阀门前后，最大流速约为2.08m/s。 随着阀门转动角度的增大，流场的高速流动区域汇聚在阀门的进出口处，使最大流速大幅增大，高达12.15m/s。 球阀进出口受冲蚀作用明显，损坏程度最大，应避免长期处于小开度的工作情况。

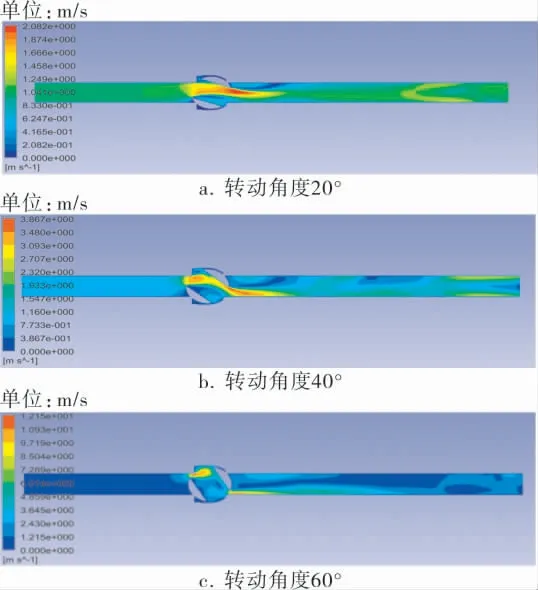
图4 球阀在不同转动角度下的xz截面速度云图

4.3 流量系数模拟值

由Fluent软件模拟结果输出的压力数据，得到不同转动角度下的压差模拟值（表5）。

表5 球阀不同转动角度下的压差模拟值

由式（12）可推导出：

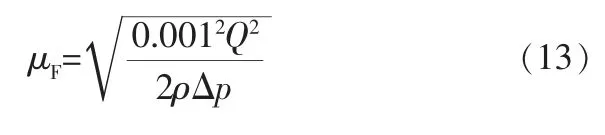
代入表5列出的压差模拟值，可以计算得出球阀不同转动角度下流量系数的模拟值（表6）。

表6 球阀不同转动角度下的流量系数模拟值

5 流量系数对比分析

根据表3、6中的数据绘制出流量系数μF模拟值和计算值的对比曲线（图5），可知μF随阀门转动角度增大而减小。 当转动角度处于0～50°时，流量系数μF快速减小，而后缓慢降低。计算值整体上大于模拟值，两曲线较为吻合，误差相对较小，采用数值模拟方法能准确显示流量系数μF随阀门转动角度变化的趋势。

图5 流量系数μF计算值与模拟值对比曲线

6 结论

6.1 对金属硬密封球阀进行流量系数理论计算，得到流量系数的初步计算值。

6.2 采用Fluent软件对球阀进行关闭过程中不同转动角度下的数值模拟计算。 随着阀门转动角度的增大，阀门前后压差增大，流场能量损失严重。 随着阀门开度的减小，贯穿阀门前后的高速流动区域转至阀门进出口， 最大流速急剧增大，对球阀的冲蚀作用逐渐增大。

6.3 通过数值模拟得到不同转动角度下球阀的压差数据，利用压差和流量系数转化公式计算出球阀流量系数模拟值，并绘制出其计算值和模拟值的对比曲线。 当阀门转动角度小于50°时，流量系数快速减小， 理论值和模拟值曲线较为吻合，采用CFD方法能有效分析球阀的流场特性。