类比思想在高中数学教学中的应用
2020-11-13寇宗娣
寇宗娣
【内容摘要】为了找到“火星上是否有生命”的正确答案,有科学家将地球与火星进行类比,发现火星的某些特征与地球很相似,如二者都是绕太阳而转;二者都存在大气层;二者都会遭遇季节的更迭,此外,大多数时间下的火星温度都适宜让地球上的某些已知生物进行生存……由此,科学家猜想:火星上也可能有生命存在。科学家做出上述猜想的推理过程就是类比推理。这种由两类对象具有某些相似或相同的属性事实出发,引入另一类同样具备这些特征的对象的推理就叫作类似推理,或简称为类比。类比推理的过程则可理解为:由特殊到特殊,由此及彼的过程。
【关键词】类比思想 高中数学 教学应用
类比作为一种重要的思维方法和推理方法,在数学发展的历史长河中占有举足轻重的地位,数学家波利亚(GeorgePolya)认为,类比对数学学习具有重要指导意义,求解立体几何问题同样有赖于平面几何中的类比问题。笔者认为在数学课堂教学中,我们必须认真审视和对待它。
在这里,笔者为大家展示一个基于“类比平面几何结论,探索立体几何性质”的假设。
如图所示:对平面直角三角形的勾股定理作类比,从而得出空间四面体性质的假设。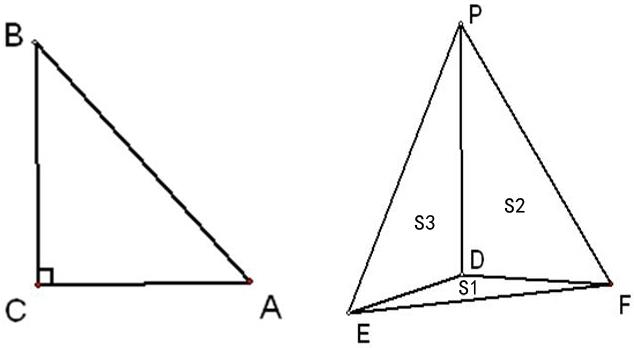
这道题的类比对象为?其分别具备怎样的特征?直角三角形内边长的关系为?在空间四面体内做类比可从哪一角度入手?
学生1:由于直角三角形两条边垂直(相互),因此,这里可选择三个面两两垂直的四面体,以此为直角三角形的类比对象。
学生2:在直角三角形中,有AC2+BC2=AB2;直角三角形中的C点对应四面体中的D点。
在四面体中有:PD2+ED2+FD2=PE2+EF2+PF2
学生3:他的结论不正确,根据边长之间的关系可以知道结论是错误的。
学生4:猜想在四面体中有以下结论:S2=S21+S22+S23
教師:很好!这个结论正确吗?可找一个特例先验证一下.
学生5:我选取DP=DE=DP=1,验证结论成立.
教师:这就增大了结论成立的可能性.但验证代替不了证明,类比结果的正确的还须严格证明。
师生共同分析:与直角三角形ABC相对应的是四面体P-DEF,与直角三角形ABC的直角边长相对应的,是四面体的面DEF,面FPD,面DPE的面积S1,S2,S3与直角三角形ABC的斜边长相对应的是四面体的面PEF的面积S。我们用长度度量线段,当然用面积度量面的大小。
在高中数学教学中类比思想也应用在很多模块中,比如等差数列与等比数列的学习、三类圆锥曲线的学习、圆与球体之间的性质对比,基本初等函数中的三类基本函数的学习,平面向量与空间向量之间的公式类比,处处渗透着类比的思想。
等差数列与等比数列是数列中的基本知识,它们之间有许多相似的地方,我们在讲授等比数列的性质时,大多数老师都用的是类比法。让学生根据学习等差数列的方法,类比得到等比数列的性质,更能促进学生对知识的理解与掌握。例如:通项公式和前n项和公式的函数性,等差中项与等比中项的性质应用。

总之,对于每一位数学老师来说,培养学生的核心素养是一项长期而艰巨的任务,类比教学,类比学习都是很好地让学生通过探索,掌握其规律的方法,从而达到举一反三的目的。所以我们必须要具备研究经验的积累,通过合情推理完成课堂教学。
【参考文献】
[1]中华人民共和国教育部.普通高中数学课程标准(2017年版)[M].人民教育出版社,2018.
[2]张乃达.数学思维教育学[M].南京:江苏教育出版社,1990.
(作者单位:甘肃省白银市第一中学)
