风电机组参与电网频率调节的策略研究

张志恒

(国网江苏省电力有限公司连云港供电分公司， 江苏 连云港222000)

0 引言

随着风力发电在我国的应用范围越来越广泛,风电不断地进入到电网中, 风电与电网之间相互影响的范围、 程度、 方式在不断深入, 带来了一系列融合问题, 如电压剧烈波动、 微机保护误动作、 频率振荡等[1-5]。

目前, 风力发电所引起的系统频率问题日益为人们所关注。 由于风电机组自身特有的解耦式控制方式, 风力机的机械动能和电网频率之间没有直接联系, 其转动惯量没有应用到电网之中, 因此电网频率的瞬时波动有所增加。 此外, 风电场输出功率的随机性和波动性, 使得电力系统需要更多的备用功率, 以满足电网频率一次调节的要求, 增加了系统的运行成本[6-7]。

针对风电所引起的电网频率问题, 国家电网公司《风电场接入电网技术规定》 要求, 风电场具备参与电力系统调频、 调峰和备用的能力, 能够实现有功功率的连续平滑调节, 并保证风电场有功控制系统的快速性和可靠性。 现代风力发电机组具备强大的控制优势, 能够适时调节自身的各种输出状态, 辅助性地解决电网中发生的各种相关问题。

1 风电机组控制策略和功率追踪模式

1.1 风电机组的控制策略

风力发电机组的控制系统包括对风轮机的控制和对变流器的控制, 其控制框图如图1 所示。 转子侧换流器能够实现对有功功率和无功功率的分别独立控制, 其有功功率控制是按照风力机控制后给出的功率指令进行, 能够实现风机转子转速的间接控制, 从而使风电机组运行在最佳转速状态, 即捕获最大的风功率。

图1 风电机组的控制框图(以DFIG 为例)

图中, 实线表示的是控制后输出信号, 虚线表示的是测量信号, 点划线表示的是给定信号； 控制给定信号用上标ref 表示, 控制反馈测量信号用上标meas 来表示。

1.2 风电机组的功率追踪模式

风轮机的所有运行状态分为四种模式, 即启动区、Cp恒定区、 转速恒定区、 功率恒定区。 一般情况下, 风轮机处于Cp恒定区, 即最大功率追踪区。 风电机组的参考功率值Pref随转子转速ωr相关的曲线如图2 所示, 其数学表达式可由公式(1)描述。

图2 风电机组的功率追踪曲线

式中,Pmax为风电机组输出最大有功；ω0为风轮机入网转速；ω1是在转速恒定区时的转速大小；ωmax为风电机的最大转速；kopt为图2 中功率追踪曲线的系数。

2 风电机组参与电网频率调节的控制策略

风电机组参与电网频率调节的控制框图如图3所示。 其在风电机组原有控制系统的基础上, 附加了风机的频率调节模块[8-12]。 此频率模块可根据电网频率的实际波动状况进行风电机组的一次调频或惯性响应控制过程。

图3 风电机组参与频率调节的控制框图

风电机组进行不同类型频率响应的判据如下:

式中,Lf、Tf是风电机组进行惯性响应和一次调频控制的阈值: 当电网的运行频率偏差较大(如Tf＝0. 05 Hz) 时, 风电机组优先进行一次调频过程,所形成的变量Δk附加在了功率追踪环节中, 使得风电机组为电网系统提供更多备用功率； 当系统频率波动较快(如Lf＝0. 03 Hz/ s) 时, 风电机组可进行瞬时的惯性响应, 风机的输出参考功率P′ref值立即发生相应变化ΔP, 以减缓电网的能量突变过程。

2.1 风电机组的惯性响应控制

从同步发电机组的惯性特征中可找到风电机组的惯性响应方法。 由同步发电机组可知, 电网频率波动时机组输出功率的变化是因为质块旋转动能的释放或吸收, 其数学表达式为:式中,Ek为机组具有的旋转动能； ΔPs为机组输出功率的变化量；J为同步机组的转动惯量；ω为机组转子的旋转角速度。

因此, 若要模拟同步发电机组的惯性特征, 风电机组则应该随系统频率的变化而改变其最大功率追踪参考值P′ref的大小, 其变化量ΔP可表达如下:

式中,Jw为风电机组的虚拟转动惯量, 其值为负数； 39. 44Jw为风电机组的惯量系数。 根据以上分析设计的风电机组惯性响应模块如图4 所示。

图4 中设置了死区, 使风电机组仅在系统频率快速变化时才启动惯性响应模块。 此模块对于系统频率的变化率按惯量系数(k1＝39. 44Jw) 形成输出功率的波动量ΔP, 因此频率变化越快, 风电机组的功率波动就越大。 最后, 功率波动量ΔP与功率追踪参考值P′ref之和将构成机组新的输出功率参考值Pref, 从而真正改变风电机组的输出功率大小。

2.2 风电机组的一次调频控制

风电机组采用一种超速减载的功率备用法, 具体过程如图5 所示。 在正常情况下, 风电机组运行于减载功率曲线PT1 上的A 点, 为电网提供一定的备用功率。 当电网频率发生变化时, 风电机组可以变换至相应的功率曲线PT2 或PT3 上, 在稳定后, 风电机组将运行于B 点或C 点, 从而增加或者减少风电机组的输出功率, 完成对系统的一次调频过程。

图5 风电机组的功率备用策略

图6 是风电机组的一次调频控制模块。 其输入量为电网实测频率f和额定频率fref, 对其偏差Δf进行比例调节, 产生Δk的值, 从而形成新的风机功率追踪曲线k′de, 改变风电机组的输出功率。 电网负荷增加, 使系统频率下降能够增大机组功率曲线系数k′de的值, 提高机组的输出功率； 电网负荷减少, 使系统频率升高, 则进行相反的过程。 通常情况下, 风电机组是在kde0＝0. 8kopt的风机功率曲线上稳定运行, 而曲线系数的变化量Δf值被限制在(-0. 2kopt, 0. 2kopt)。 此外, 电网频率处于(50-Δfmin, 50+Δfmin) 时, 风机将处于一次调频的死区, 即曲线系数变化量Δk为0。

图6 风电机组的一次调频模块

惯性响应与一次调频控制使风电机组参与了电网频率的调节, 为系统频率的控制发挥了风电自身的作用, 从而增强了系统频率的稳定性。

3 风电机组频率控制策略的仿真分析

针对一含风电的电网仿真系统, 其结构如图7 所示, 包含一个风力发电场G3和两个火力发电厂G1、 G2, 在系统中共有3 处有功负荷(L1、L2和L3), 火力发电厂G1和G2均配有励磁系统和有功控制系统, 在风电机组的功率控制系统中加入频率控制模块, 通过对风电机组惯性和一次调频的仿真分析, 可验证风机频率控制策略的有效性。 此仿真模型中各风电场机组的参数见表1—2。

图7 仿真系统结构

表1 风机参数

表2 同步发电机G1、 G2 参数

3.1 风机惯性响应过程的仿真分析

初始时风电机组及电网系统处于稳定运行状态, 风速稳定为7 m/ s。 在3 s 时电网出现500 ms时长40 MW 大小的有功功率投切, 电网频率和风电机组输出功率的仿真结果如图8 所示, 其中虚线表示风机无惯性响应控制策略, 实线表示有惯性响应控制策略时的情况。

图8 风电机组的惯性响应

从图8 可知, 系统频率的快速下降引发了风电机组的惯性响应控制, 图8 (b) 的仿真结果说明,在惯性响应的过程中, 风电机组通过风机转速的快速降低, 其输出功率会突然增加, 形成了对系统频率变化的有效惯性响应, 因此频率的波动比机组没有惯性控制时有所减缓(图8 (a) )。

3.2 风机一次调频过程的仿真分析

初始时风电机组及电力系统处于稳定运行状态, 风速恒定为7 m/ s。 从3 s 时电力系统开始增加50 MW 负荷并引起电网频率的下降, 系统频率和机组输出功率的仿真结果如图9 所示, 其中实线表示风电机组有一次调频控制策略, 虚线表示风电机组无一次调频控制策略的情况。

图9 风电机组的一次调频

从图9 可知, 在风电机组参与一次调频之后,机组的转速降低, 同时机组的输出功率增加, 风电机组释放了备用功率从而减缓了电力系统中的功率不平衡状况。 由于风电机组的一次调频控制, 系统频率与额定值的偏差没有一次调频控制时缩小, 因此电网频率的响应结果有了显著的改善。

3.3 风机综合调频过程的仿真分析

初始时风速恒定为7 m/ s, 风电机组稳定运行于功率追踪区, 电力系统处于供电-负荷的平衡状态。 在3 s 时电网开始增加50 MW 的有功负荷, 系统因功率失衡而产生频率波动, 风电机组参与系统频率调节的仿真结果如图10 所示, 其中实线表示有频率控制策略时效果, 虚线表示无频率控制策略时效果。

在电网负荷增加时, 系统频率会首先快速降低, 之后再稳定运行于某一频率值上。 因为在系统频率快速下降时, 风电机组进行了惯性支持, 所以电网频率的初始下降速率将有所减缓。 之后风电机组又根据电网频率的偏差进行了一次调频控制, 调整了机组功率追踪曲线系数, 从而缩小了系统频率与额定值(50 Hz) 的偏差。 图10 (a) 显示在风电机组附加频率控制模块后, 电网频率的响应效果变好, 频率下降变得缓慢且频率的稳态偏差变小。总之, 引入本文的频率控制策略后, 风电机组可根据系统频率的不同波动情况进行惯性支持、 一次调频支持, 或者先后进行惯性响应和一次调频支持, 提供对系统频率的辅助调节功能, 电网频率的响应效果变得更好。 因此, 在高风电渗透率地区,风电机组可附加本文的频率控制模块。

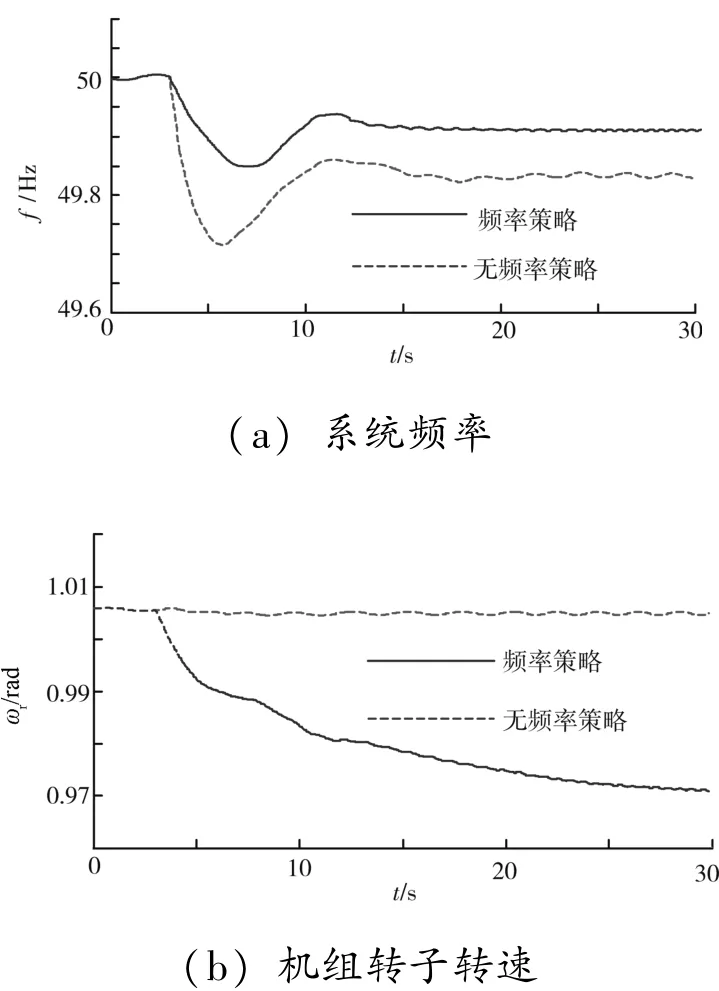
图10 风电机组的频率响应结果

4 结论

本文通过惯性控制和一次调频相结合的方法设计了风电机组的频率控制策略。 风机惯性响应控制是通过在风电机组输出功率的参考值上附加惯性变量来完成的, 而一次调频控制则是通过改变机组的功率曲线从而提供备用功率。 这两种调频策略相互补充、 相互协调, 实现风电机组具备与传统机组相似的频率响应特性, 从而可以使电网频率更加稳定。 利用一个电力系统模型的仿真分析, 证明本文所提出的惯性控制与一次调频结合的调频控制策略具有有效性, 风力发电机组可对电网频率提供动态支持, 保证电网的稳定性。