波能装置与浮式防波堤集成系统的水动力性能

2020-11-13张恒铭胡俭俭周斌珍刘品

哈尔滨工程大学学报 2020年8期

张恒铭，胡俭俭，周斌珍，2，刘品

(1.哈尔滨工程大学船舶工程学院，黑龙江哈尔滨 150001； 2.华南理工大学土木与交通学院，广东广州 510641)

振荡浮子式波能装置是目前转换效率较高的一种波能装置，但其建造成本高、维修困难等缺点导致波浪能发电的成本远高于传统的热力发电(如煤炭，天然气)和其他可再生能源发电[1-2]。浮式防波堤以其受海底地质条件影响小、对环境影响小等优点被广泛的使用[3]。但浮式防波堤主要依靠反射波浪和耗散波浪来实现消波的功能，且其宽度至少需要达到波长的三分之一才能满足消波的要求，这就导致了长波条件下浮式波堤建造成本的提高[4]。由于波能装置与浮式防波堤在功能上具有一定的相似性和相容性，因此文献[5]提出将两者集成进行研究，这样既能实现成本分摊，还能实现发电功能与消波功能集成[5-8]。研究人员对该种集成装置进行了研究[9-10]，但大部分采用的都是基于势流理论和实验的方法，如Madhi等[11]应用实验的方法研究了一种Berkeley-Wedge形装置；Ning[12]通过实验方法研究了方箱型的集成装置的性能；Zhao[13]应用实验的方法对比研究了单浮体集成装置与双浮体系统的防波性能和波能捕获效率；Ning等[14]基于线性势流理论和匹配本征函数展开法研究了双浮筒装置的水动力性能及其影响因素；He等[15-16]采用实验方法开展了振荡水柱式波浪能装置与浮式防波堤集成系统的水动力研究。

浮子形状对集成装置的水动力性能有较大影响[15-18]，因此本文针对WEC-防波堤集成系统的浮子形状对装置水动力性能的影响展开研究。由于势流理论忽略了流体的粘性，导致计算结果不准确，尤其是在浮子的共振频率附近[19]，而实验的成本高、耗时多。耿静等[20]对U-OWC波能装置的研究中将Star-CCM+软件的结果与实验结果进行了对比，结果吻合良好，因此本文使用粘性计算流体力学(computational fluid dynamics，CFD)软件Star-CCM+建立二维数值波浪水槽模型，研究浮子形状对集成系统的运动响应、转换效率、反射系数、透射系数以及耗散系数的影响，以达到提升其防波性能和发电性能的目的。

1 透射系数、反射系数及转换效率等参数定义

固有频率ωn及单个浮子的线性最优阻尼系数bopt的分别为[21-23]：

(1)

(2)

式中：az和bz分别为附加质量和辐射阻尼；cz=ρgAw为恢复力系数；cpto为动力输出装置(power take-off, PTO)系统的刚度系数；m为浮体质量；ω为波浪频率。

波能装换装置的转换效率ηe为[21]：

ηe=Ep/Ew

(3)

式中：Ep为波能装置的平均波浪能转换功率；Ew为入射波的平均功率[21-22]。

浮子的运动响应定义为浮子运动幅值HRAO与入射波高Hi的比值：

ζ=HRAO/Hi

(4)

波能装置的透射系数Kt和反射系数Kr分别定义为：

Kt=Ht/Hi

(5)

Kr=Hr/Hi

(6)

式中：Ht为透射波高，Hi为入射波高，Hr为反射波高。反射波高通过“两点法”[24]得到，2个波高监测点放置在浮子迎浪面一侧，距离浮子分别为1.6 m和2.4 m。

耗散系数表达式为：

(7)

2 模型参数设置及验证

2.1 模型计算域和边界条件设置

图1为本文所用二维数值波浪水槽模型示意图。水槽横向的长度选取为6倍波长，垂向的高度取2倍水深。由于Star-CCM+软件无法直接模拟二维波浪水槽模型，因此模型纵向宽度设置为0.01 m。模型左右两端分别设置1.5倍波长的造波区和消波区，两端的消波方式设置为力消波。边界条件的具体设置参考文献[25-26]。

图1 模型计算域和边界条件设置示意Fig.1 A diagram of computational domain and boundary conditions applied to the model

2.2 模型网格划分

本文在划分网格时，选用切割体网格单元生成器和棱柱层网格生成器来对模型进行网格划分，生成的网格如图2所示。液面加密区高度为1.5倍波高，液面过渡区为3倍波高。在物面周围设置10层棱柱层，总厚度为一个网格的宽度。

图2 波浪水槽模型网格生成图Fig.2 Mesh generation details of the wave tank model

2.3 模型收敛性与准确性验证

对于本文所建立的CFD数值模型，需要确定合理的网格尺寸和时间步长，使计算结果满足收敛性要求。

本文针对单个浮式方箱与波浪相互作用模型的网格尺寸和时间步长的收敛性进行了验证。方箱的宽度和吃水分别为B/h=0.8和D/h=0.2。设置3个模型：模型A，模型B，模型C，模型水深为h=1 m，入射波高为Hi=0.2 m，波浪周期选取为T=1.37 s。3个模型的时间步长和网格尺寸如表1所示。

表1 方箱形浮子时间步长和网格尺寸

3个模型中浮式方箱的位移曲线如图3所示。由图可知，3条曲线基本吻合，仅在峰值和谷值处存在细微差别，且误差小于5%，说明3个模型的网格尺寸和时间步长都满足收敛性要求。为了节约计算时间，选用模型A的时间步长和网格尺寸来进行接下来的研究。

图3 浮式方箱模型的网格和时间步长的收敛性研究Fig.3 Convergence study on mesh and time step of a floating square box model

为保证模型的入射波满足要求，本文对水槽中波面衰减情况进行了研究。图4给出了水槽空域模型沿波浪传播方向的波高分布，模型水深1 m，入射波高0.2 m，波浪频率4.58 rad/s。由图4可知，波浪沿传播方向衰减很小，波高最大衰减仅为3.5%，因此本文所用数值水槽模型的造波能力满足要求。

图4 空域模型波浪高度的空间分布Fig.4 Spatial distribution of wave heights of the model without a floating body

为了验证模型的准确性，本文使用建立的CFD数值模型对文献[12]中的实验进行了模拟，模拟结果如图5所示。图中也同时给出了文献[27]的解析解结果。

图5 不同数值模型计算结果与文献[12]的实验结果对比Fig.5 Comparison between the different numerical results and the experiment results of ref. [12]

从图中可以看出，由于文献[27]的解析模型忽略了粘性效应[28]，导致结果比实验结果大，尤其是在共振频率附近，而本文的CFD模型考虑了粘性效应，使得本文数值结果与文献[12]的实验结果吻合较好。因此本文采用考虑粘性效应的CFD数值模型进行接下来的研究。

2.4 最优阻尼系数验证

本文以2.3节中的方箱模型为例，对最优阻尼系数进行了验证。波浪频率设置为ωn=4.22 rad/s，波高Hi=0.2 m，PTO阻尼系数分别取bpto/bopt=0.69，0.90，1.0，1.1，1.2。图6给出了不同PTO阻尼下方箱的转换效率。

图6 方箱形模型的转换效率随PTO阻尼系数的变化Fig.6 Variations of conversion efficiency versus PTO damping coefficient of a box-type model

由图可知，当bpto/bopt=1时，即PTO阻尼为最优阻尼时，方箱模型的转换效率是最高的，验证了公式(2)所求最优阻尼的正确性。

3 浮子形状对水动力性能的影响

结合文献[11-12，27]的研究可以看出，浮子底部形状是影响装置性能的重要因素。本文应用Star-CCM+软件所建立的CFD模型，研究了4种浮子底部形状对集成装置的防波性能和发电性能的影响。

入射波浪波幅A=0.1 m，水深h=1.0 m，浮子模型底部形状和尺寸如图7所示。

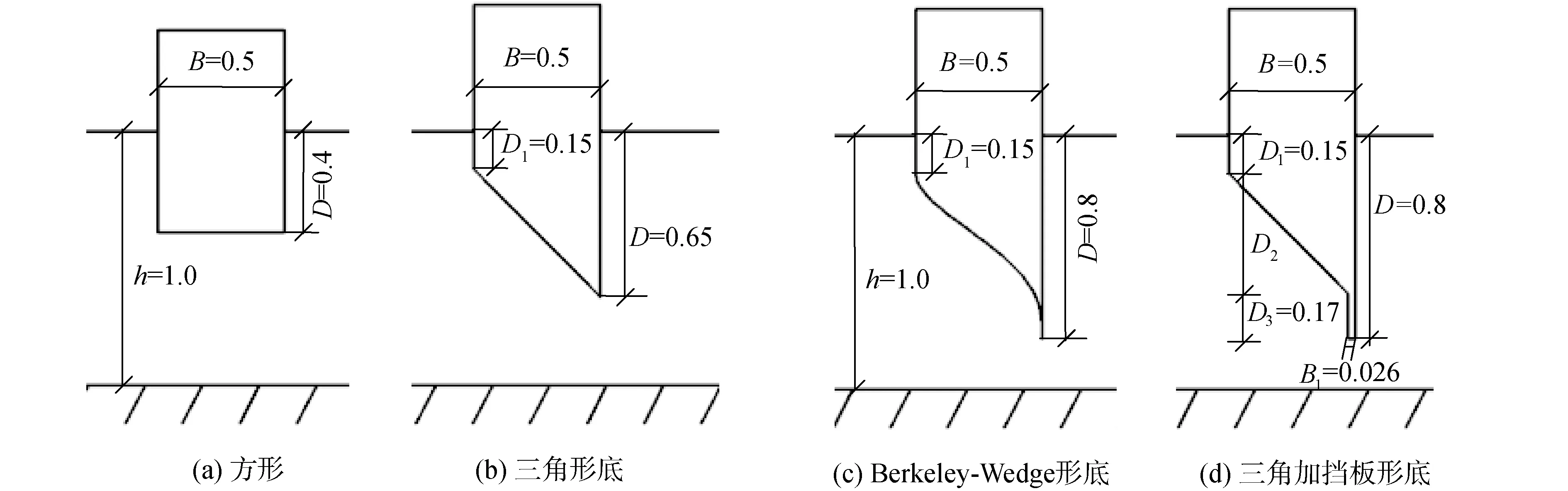
图7 4种不同底部形状浮子的尺寸示意Fig.7 Schematic diagram of floaters with four different bottom shapes

图8为具有不同底部形状的浮子在最优PTO阻尼下的运动响应ζ、转换效率ηe、透射系数Kt等变量随频率ω的变化关系。

由图8可以看出知，当波浪频率增大时，4种形状的浮子的运动响应ζ和波能转换效率ηe都呈现出先增大后减小的趋势。转换效率ηe在共振频率处达到最大值，而运动响应的峰值不在共振频率处。对于透射系数来说，当频率增大时，4种浮子的透射系数Kt会一直减小，说明频率越高，浮子的防波性能越好。在3.0～4.5 rad/s的频率范围内，Berkeley-Wedge形浮子的透射系数最小，转换效率最高，最高达到86.7%，而方形浮子的透射系数最大，转换效率最低，最大仅为21%。

图8 不同形状浮子在最优PTO阻尼下ζ、 ηe、 Kr、 Kt and Kd随频率变化Fig.8 Variations of ζ, ηe, Kr, Kt and Kd versus ω for different bottom shapes under the optimal PTO damping

由于Berkeley-Wedge形浮子的底部形状为复杂的曲面，不便于加工制造。为了得到高性能且易于加工制造的浮子形状，在保证质量不变的情况下将Berkeley-Wedge形浮子底部形状简化为三角形。由图8可知，在ω>4.5 rad/s的高频范围内，三角形浮子的转换效率以及透射系数与Berkeley-Wedge形浮子的差别很小；而在ω<4.5 rad/s的频率范围内，三角形浮子的透射系数更大，转换效率更小，说明在此频率范围内三角形浮子的发电和防波性能比Berkeley-Wedge形浮子差。由于入射波的水质点速度和能量都随水深的增加而减小，频率越高，衰减越快，在水下一定深度就衰减为0。三角形浮子与Berkeley-Wedge形浮子的吃水较大，因此在ω>4.5 rad/s的高频波中，两浮子底部形状的差异对其透射系数和转换效率的影响甚微。同时这2种形状的浮子对于能量的耗散几乎相同，如图8(e)所示，因此三角形浮子在高频波中的转换效率与Berkeley-Wedge形浮子基本相同。而低频波的水质点速度和能量沿水深方向衰减很慢，在水深较大处才衰减为零，因此在ω<4.5 rad/s的频率范围内，吃水更大的Berkeley-Wedge形浮子对水质点速度影响越大，且与之相互作用的波能也越多，从而导致其转换效率比三角形浮子更高，透射系数比三角形浮子更低。

根据以上的结果可知，浮子的吃水是影响波能装置发电性能和防波性能的一个重要因素。因此，为了提高三角形浮子在低频波作用下的发电性能和防波性能，在其底部增加一块薄的挡板来增加吃水。加装挡板后的三角形浮子的吃水与Berkeley-Wedge浮子相同，如图7(d)所示，这种新型浮子命名为三角加挡板形浮子。由图8(b)和图8(c)可知，与三角形浮子相比，挡板的存在使得三角加挡板形浮子的转换效率明显增大，透射系数明显减小。三角加挡板浮子的运动响应、转换效率和透射系数都与Berkeley-Wedge形浮子非常接近，仅在共振频率处有微小差别，且两者的反射系数随频率的变化趋势也基本相同。三角加挡板形浮子和Berkeley-Wedge形浮子在共振频率下的最大转换效率分别为82.5%和86.7%。