减阻剂溶液注入对回转体通气空化的影响
2020-11-13王璐郑智颖刘平安李玩幽
王璐, 郑智颖, 刘平安, 李玩幽
(1.哈尔滨工程大学 航天与建筑工程学院,黑龙江 哈尔滨 150001;2.哈尔滨工业大学 能源科学与工程学院,黑龙江 哈尔滨 150001;3.哈尔滨工程大学 动力与能源工程学院,黑龙江 哈尔滨 150001)
水下航行体以超空化状态航行时,其阻力可以减小90%,从而实现其高速航行。超空化减阻技术的关键在于快速且稳定地形成气液交界面。目前,通常依靠人工通气的方法增加空泡内压强从而生成通气超空泡。然而,在一定的航行速度下,通气超空泡减阻的效果也存在极限值。贺杰[1]发现减小气液交界面处的表面张力,空泡将快速生长并保持稳定以减少其溃灭的频率。研究表明:添加某些表面活性剂溶液可以降低了水的表面张力[2]。此外,某些表面活性剂还具有湍流减阻效应,阻力减小程度最大可达90%[3]。故可以采用表面活性剂溶液促使空化快速达到超空化状态。
针对表面活性剂溶液对空化特性的影响,邹志林[4]和李凤臣[5]开展了大量的数值模拟和实验研究。在表面活性剂溶液中运行的水下航行体,其空泡长度和直径均大于相同条件下水中的空泡尺寸,并且流动阻力明显减小。对在表面活性剂溶液中的水下航行体进行通气空化,发现空泡的尺寸增加,主要减小了空化发展阶段的摩擦阻力[6]。在注入表面活性剂溶液的情况下,通气空泡的尺寸仅略微增加,且减阻效果也并不明显[6-7]。这可能是由于表面活性剂溶液的注入位置在空泡内,并没有直接作用于气液交界面处。在实际当中,由于受限于动力和速度等因素,水下航行体难以通过自然空化实现带超空泡稳定持续航行,因而大多通过在低速下在航行体的某些特定位置通气以达到超空泡状态,并最终实现航行体的带超空泡高速航行。在不考虑通气的情况下,水下航行体的高速航行也将引起自然空化的发生。因此,水下航行体以通气超空泡状态高速运行时,将可能出现通气空化和自然空化并存的状态。然而,目前针对水下航行体高速下通气超空泡的很多研究均只考虑了通气空化气液两相流。因此,本文考虑自然空化可能并存下的通气空化气-汽-液三相流动。为了使表面活性剂减阻溶液主要作用于空泡的气液交界面,本文将表面活性剂溶液的注入位置设定在通气位置之前,研究通气和注入减阻剂溶液对局部空化和超空化的影响,旨在探究以表面活性剂作为减阻剂的注入对回转体通气空化特性的影响。
1 空化数值计算控制方程
水下航行体在水中的运动是一种典型的湍流问题,为了使研究结果为工程实际应用提供一定线索,本文采用了工程上广泛使用的雷诺平均数值模拟(Reynolds average navier-stokes,RANS)方法进行数值模拟,采用了SSTk-ω湍流模型。对于空化多相流采用了具有无滑移假设的Mixture多相流模型,具体的控制方程表示为:
(1)
(2)
(3)
式中:αp为第2相p的体积分数,本文中主要考虑了液态水w、水蒸气v、空气a和减阻剂溶液s共4相。其中,主相为液态水,其他3相为第2相,则p可以为v、a或s,且对于空气相a,式(3)等号右边的2项均为0。ρm和μm分别为混合相的密度和粘度:
(4)
(5)
式中:αk、ρk和μk分别为各相的体积分数、密度和粘度,则k可以为w、v、a或s,且各相体积分数满足:
(6)
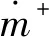
(7)
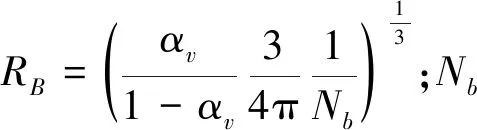
本文旨在研究注入表面活性剂减阻溶液对回转体通气空化特性的影响,在数值模拟过程中,需要描述表面活性剂溶液剪切粘度随剪切率变化的剪切稀变特性。而现有的针对广义牛顿流体湍流的直接数值模拟[8]结果表明,剪切稀变特性对管内湍流的影响同粘弹性流体的湍流减阻效应相似,因此已有研究[9-10]采用Cross粘度模型模拟粘弹性流体减阻湍流。此外,现有的采用Cross粘度模型开展减阻溶液入水空化数值模拟[11-12]的计算结果同实验结果亦符合很好。因此,本文采用了广义牛顿流体模型Cross粘度方程描述表面活性剂减阻溶液的剪切粘度随剪切率增大而减小的剪切稀变特性:
(8)
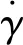
2 计算模型及条件
本文所研究的水下航行体为轴对称回转体,如图1所示。在数值模拟计算时,为了减小计算量,根据其轴对称结构,对图1所示的模型进行了二维数值模拟。图中还给出了计算中采用的笛卡尔坐标系和边界条件的设定,其中,计算域的入口设置为速度入口,速度方向垂直入口;计算域的上界面设置为速度入口,速度大小与计算域入口速度大小相同,方向沿x轴;出口设置为压力出口且压强为101 325 Pa。当数值模拟自然空化时,水下航行体壁面均设置为无滑移边界;当数值模拟通气空化时,通气孔设置为速度入口,速度与来流速度方向成15°;当数值模拟减阻剂溶液注入下的通气空化时,溶液注入孔亦设置为速度入口,且速度方向沿y轴。由于计算域较大,网格较密,图2只给出了计算域中水下航行体头部和艉部附近的网格分布。本文中采用结构化网格划分计算域,并且对近壁区的网格进行了加密处理,近壁区的第1层网格以满足SSTk-ω湍流模型对近壁区第1层网格y+值的要求(y+<1),最终网格数总为744 240。
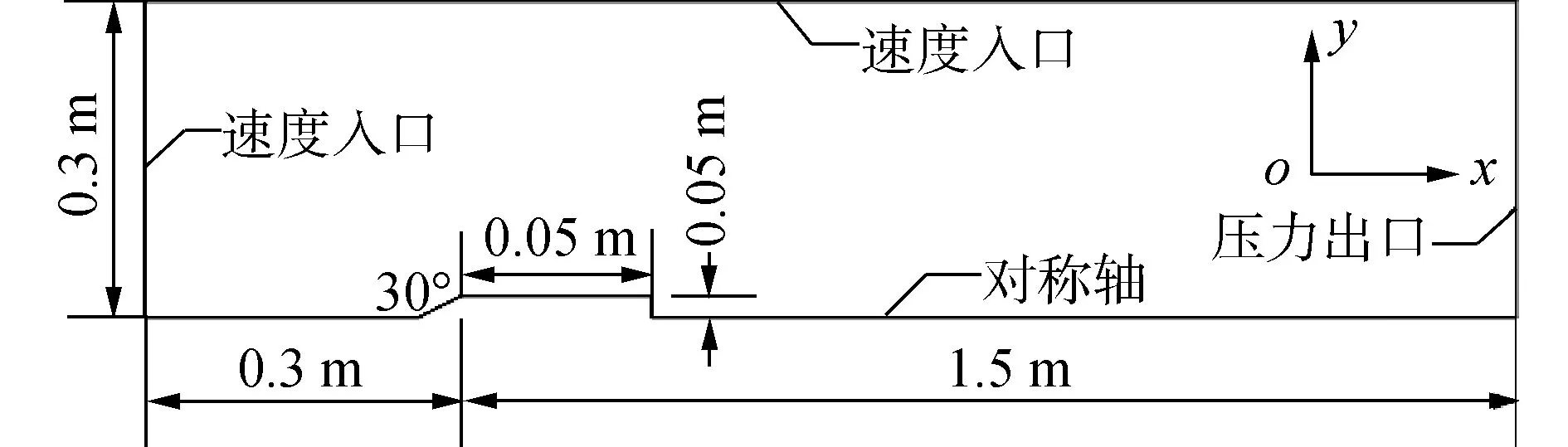
图1 回转体及计算域Fig.1 Axisymmetric body and the computational domain
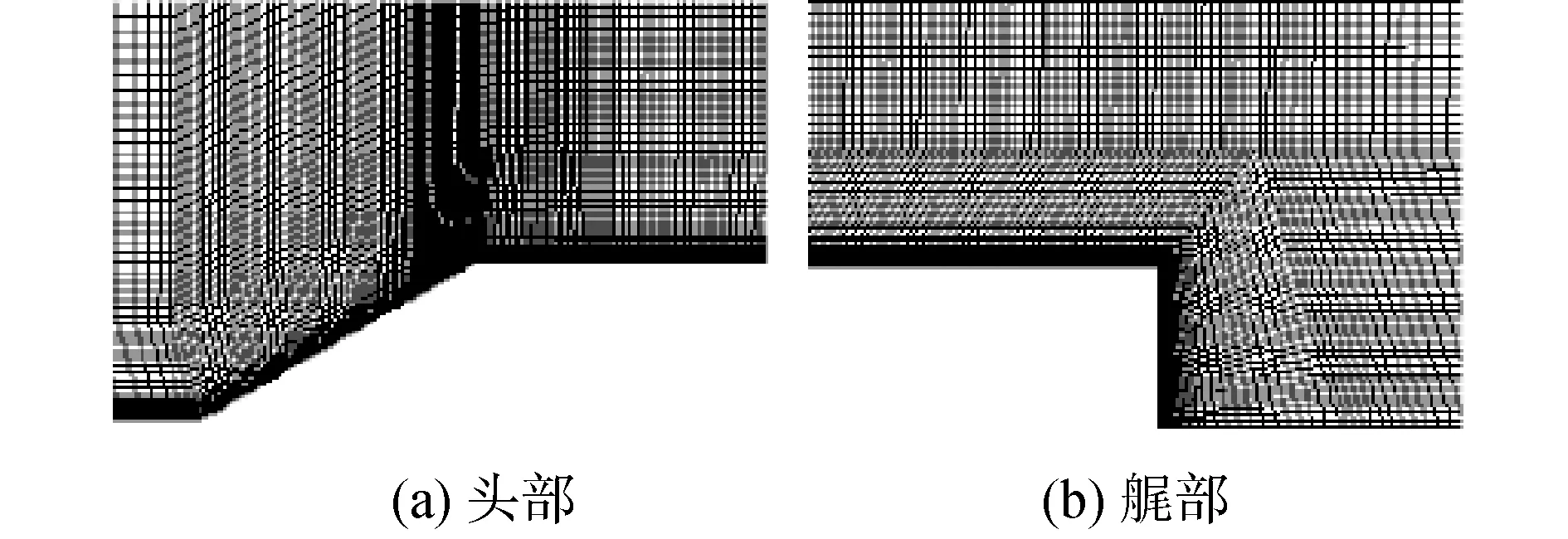
图2 回转体附近网格Fig.2 The mesh near the axisymmetric body
对于离散格式,本文采用SIMPLEC算法计算压力与速度的耦合,具体方案为:压力选用适于求解空化流动的PRESTO!格式,动量方程、k方程和ω方程均选用二阶迎风格式,体积分数方程选用一阶迎风格式。
在数值模拟中,本文选用水和水蒸汽热力学性质国际标准[14]中的25 ℃下水和水蒸汽的物性参数作为液态水相和蒸汽相的热力学参数。而由于减阻剂溶液中表面活性剂的浓度很低,因此其密度和饱和蒸汽压可视为与液态水的物性相同。综上,数值计算中各相的具体物性参数如表1所示。

表1 水、水蒸汽、空气和减阻溶液的物性
3 数值计算结果与讨论
3.1 通气和溶液注入位置的确定
为了确定回转体表面通气和减阻剂溶液注入的位置,需要获得无空化流动状态下回转体表面压力最小的位置,这是因为空化初生在压力最小处,且在压力最小处进行通气和减阻剂溶液注入可节省动力,实现方式也更为简便。图3给出了无空化状态下回转体周围的无量纲压力分布云图:
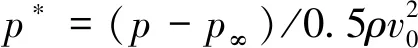
(9)
式中:p∞为环境压力且p∞=101 325 Pa;v0为来流速度。
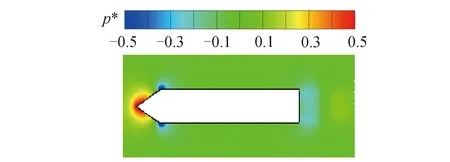
图3 回转体周围无量纲压力分布Fig.3 Distribution of dimensionless pressure around axisymmetric body
从图中可以看出回转体锥形头部与圆柱主体相接处的压力最小,因而可在此处设置通气孔和溶液注入孔。为了确保注入的减阻剂溶液可以直接作用于空泡的气液交界面,将减阻剂溶液注入孔设置在通气孔之前,如图4所示,其中通气孔位于回转体圆柱主体的最前端且宽度为0.003 m,溶液注入孔位于回转体锥形头部的末端且宽度为0.002 m。

图4 回转体上通气孔和减阻剂溶液注入孔位置的示意Fig.4 Schematic diagram of the locations for the ventilation and injection of drag-reducing solution
3.2 初生空化数的确定
在研究空化流动时,通常使用空化数σ来描述空化的程度。为了方便界定下文中的局部自然空化和自然超空化,本文用自然空化数为:
(10)
在分析注入减阻剂溶液对回转体通气空化流动特性的影响之前,本文数值模拟了不同来流速度下的自然空化工况,如表2所示,以确定初生空化数和不同来流速度下的自然空化状态,并通过与已有结果的对比验证本文数值方法的有效性和正确性。
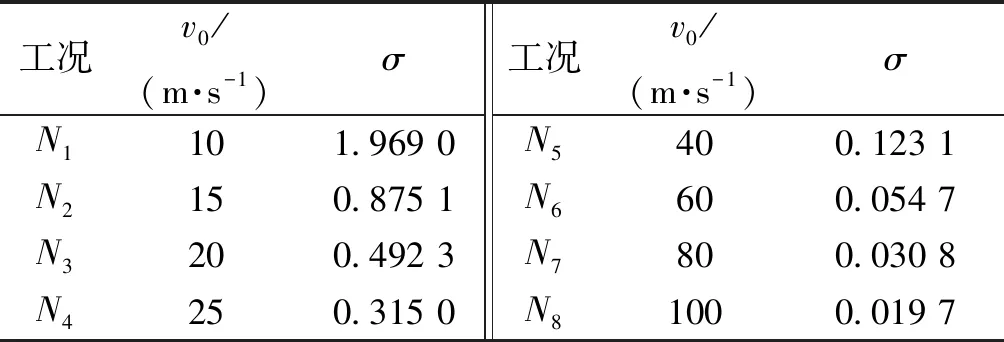
表2 自然空化工况Table 2 Cases of nature cavitation
图5给出了自然空化工况下空泡的无量纲直径Lc/D和无量纲长度Dc/D(D为回转体直径),同时与Guzevsky经验公式[15]的结果作比较。在本文中,超空泡长度定义为空泡产生位置到空泡末端之间的距离,直径定义为空泡最大横截面处的直径,而空泡轮廓则根据气相体积分数αg=0.1(气相体积分数αg为蒸汽相αv和空气相αa体积分数之和,对于本节的自然空化,空气相体积分数αa=0)的等值面确定。从图5可以看出,本文的计算结果与经验公式结果相符,从而说明了上述数值计算方法的合理性。
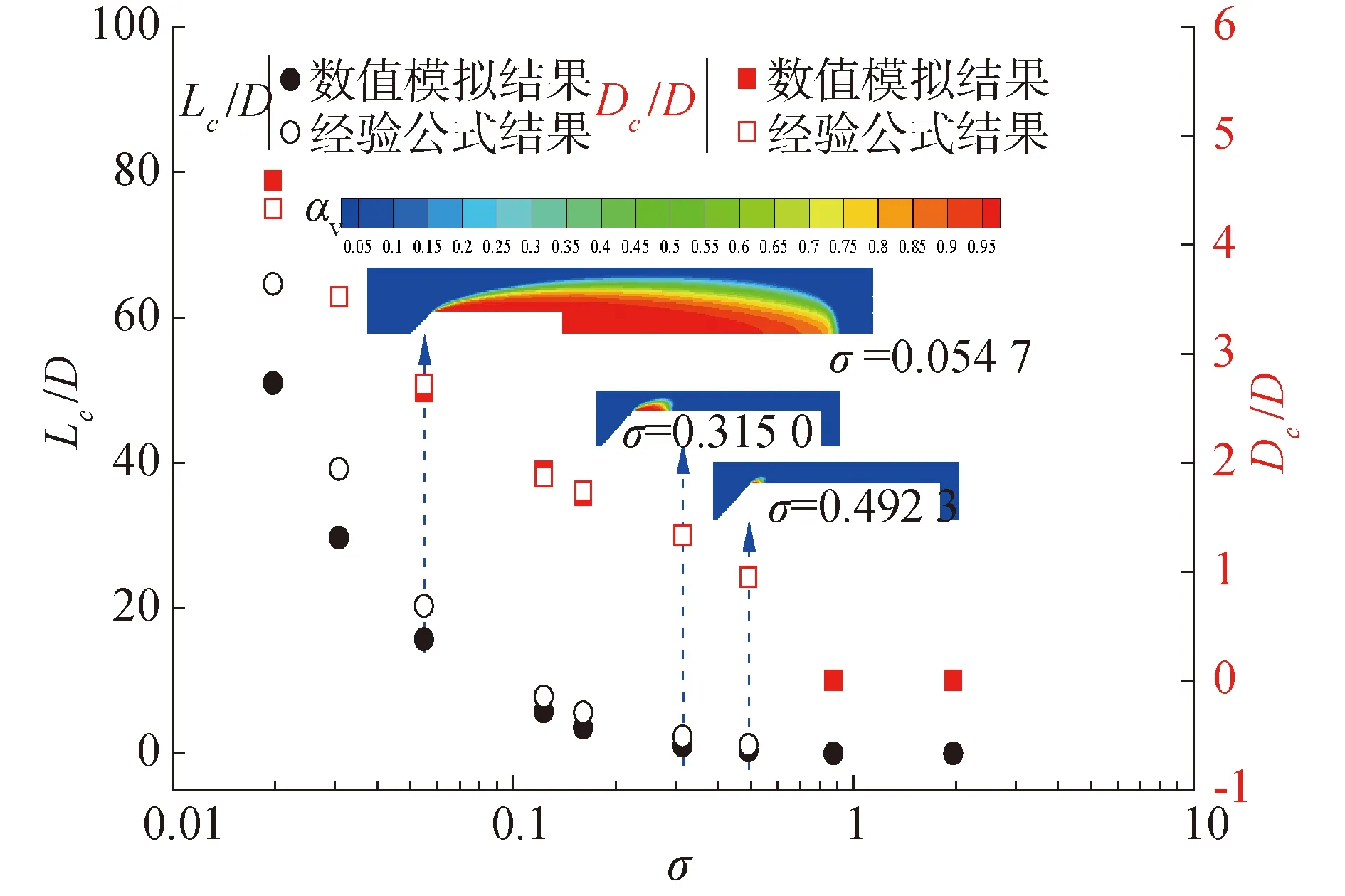
图5 不同空化数下自然空化的空泡无量纲直径和无量纲长度以及水蒸汽体积分数云图Fig.5 Dimensionless diameters and lengths of the natural cavities and contours of vapor phase volume fraction under different cavitation numbers
空化流动的状态按照发展阶段可以分为初生空化、局部空化和超空化。为了研究注入减阻剂溶液对回转体空化特性的影响,尤其是局部空化和超空化,需要确定初生空化这一临界状态所对应的初生空化数σi。图5为初生空化、局部空化和超空化3个典型工况下的水蒸汽体积分数云图。从图中可以看到,在σ=0.492 3时水下航行体周围出现极小空泡,之后随着空化数的减小,回转体周围的空泡尺寸(包括空泡直径和长度)增大,在σ=0.054 7时空泡包裹了整个水下回转体,即达到超空泡状态。同时,从图5中自然空化的空泡无量纲长度和直径随空化数的变化也可以看出,空泡是从σ=0.492 3开始形成的。从上述分析可知,初生空化数σi=0.492 3。
为了研究注入减阻剂溶液和通气对水下回转体局部空化和超空化流动特性的影响,选取了σ=0.315 0局部空化(工况N4)和σ=0.054 7超空化(工况N6)作为下文研究中的2个典型工况。
3.3 通气对空化特性的影响
本文探究了通气对水下回转体局部空化(σ=0.315 0)和超空化(σ=0.054 7)流动特性的影响。选取了通气体积流量Qa以表征通气量的大小:
Qa=vaπDLa
(11)
式中:va为通气速度;La为通气孔宽度(如图4所示)。本文所研究的水下回转体通气空化的具体工况如表3所示。

表3 通气空化工况Table 3 Cases of ventilated cavitation
图6给出了相同空化数下回转体自然空化与通气空化液相体积分数(本文中液相体积分数αl定义为液态水相和溶液相体积分数之和,即αl=αw+αs,对于本小节的通气空化,溶液相体积分数αs=0)分布的比较结果,其中每幅图的上下2部分分别对应通气空化工况和自然空化工况。从图中可以看出,在相同通气量下,通气明显增大了局部自然空化(σ=0.315 0)下的空泡直径和长度,在通气量为9.42×10-4m3/s(如图6(a)所示)时通气后形成的空泡形态已经将回转体完全包裹;然而,当自然空化为超空化(σ=0.054 7)状态时,通气对空泡的形态影响甚微,甚至通气量在2.83×10-3m3/s(如图6(d)所示)时通气后形成的空泡长度比自然空化下的空泡长度稍小,这可能是由于通气破坏了气液交界面的稳定性。进一步比较图6(a)和图6(b)还可以发现,随着通气量的增加,空泡的直径增大,回转体主体周围的液相体积分数减小。
对于水下航行体而言,其所受到的阻力是另外一个至关重要的性能参数,若阻力减小,则可提高航速或者承载量。在空化流动研究中,通常使用摩擦阻力系数Cv、压差阻力系数Cp和总阻力系数Cd来描述水下航行体的阻力特性:
(12)
(13)
(14)
式中:Fv、Fp和Fd分别为摩擦阻力、压差阻力和总阻力;A为迎流面积,在本文中定义为回转体主体横截面积,即A=0.25πD2。根据上述公式,式(12)、(14)分别计算了自然空化工况和通气空化工况下回转体的各阻力系数,如图7所示。从图中可以看出,对于局部空化(σ=0.315 0)工况,相对于自然空化,通气明显减小了Cv,并且随着通气量的增大,Cv进一步减小,这是由于通气量的增加减小了回转体主体周围的液相体积分数(如图6(a)和(b)所示);而通气对Cp的影响不大。因此,摩擦阻力的减小使通气空化工况的总阻力小于自然空化工况的总阻力。然而,对于超空化(σ=0.054 7)工况,不论通气与否以及通气量的大小,Cv、Cp和Cd的变化均很小,说明通气并未影响其阻力特性,这与图6得到的结果一致。上述分析说明通气对空泡生长的促进作用主要适用于局部空化工况。
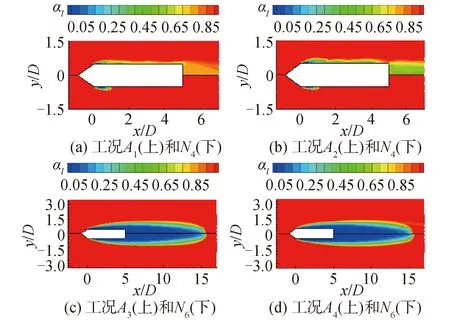
图6 相同空化数液相体积分数分布Fig.6 Distributions of liquid phase volume fraction in ventilated cavitation and natural cavitation under different cases
3.4 通气和溶液注入对空化特性的共同影响
本文研究通气和溶液注入对回转体周围空化流动特性的影响。类似地,同样定义了溶液注入的体积流量Qs以表征减阻剂溶液的注入量:
Qs=vsπDLs
(15)
式中:vs为注入减阻剂溶液的速度;Ls为溶液注入孔的宽度(如图4所示)。本文对同时通气和注入溶液影响回转体空化特性的研究工况如表4所示。
通过已有研究结果[6-7]可知,当通溶液位置位于通气位置之后时,通入的减阻溶液并未真正作用于空泡的气液交界面,意味着减阻溶液并未降低空泡气液交界面处的表面张力。因此,在开展下一步研究之前,需要确认注入的减阻溶液是否作用于空泡的气液交界面处。图8给出了工况AS1下同时注入溶液和通气时回转体周围溶液相和气相的体积分数分布。可以看出,注入的减阻剂溶液分布于空泡的气液交界面,实现了表面活性剂溶液促进空泡生长的目的。这也说明了本文采用的减阻剂溶液注入位置位于通气位置之前这一布置方式的合理性。
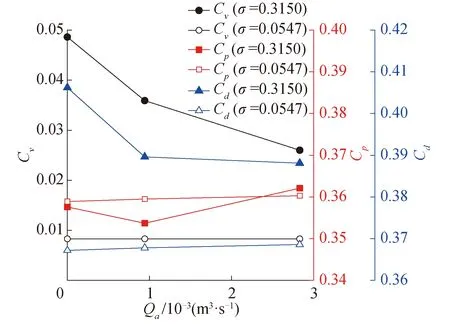
图7 不同通气量下自然空化与通气空化的阻力系数Fig.7 Drag coefficients of nature cavitation and ventilated cavitation at different ventilation flow rate

表4 减阻剂溶液注入下通气空化工况
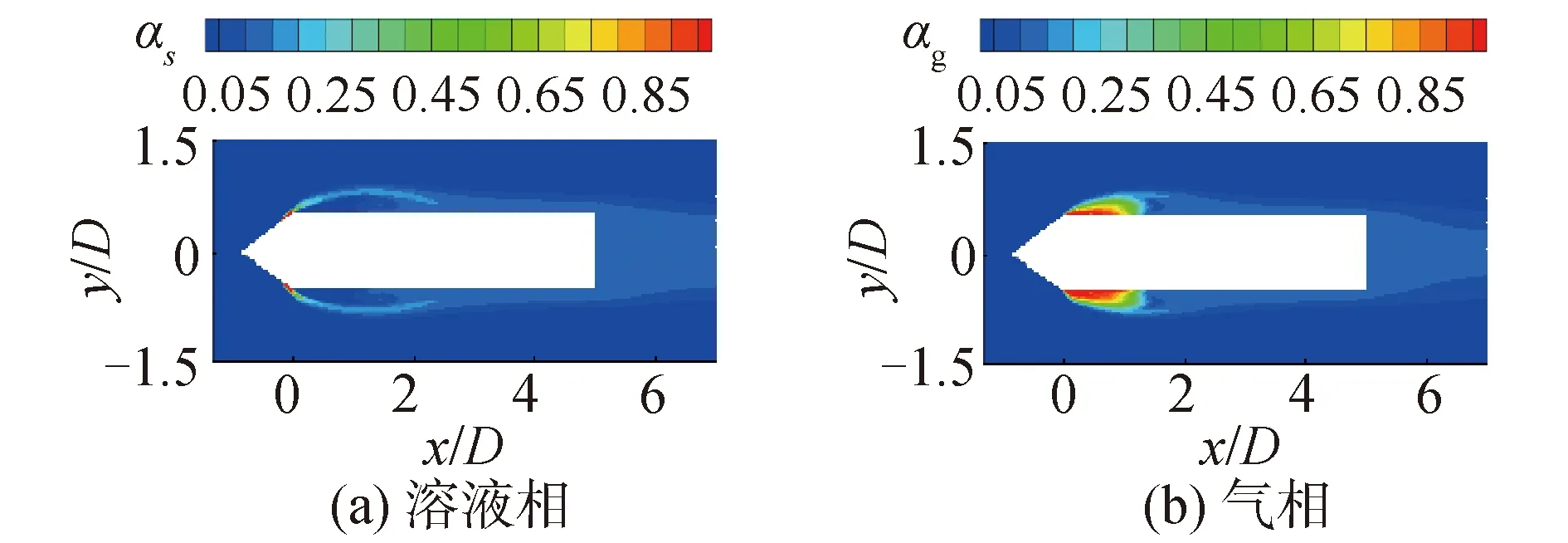
图8 工况AS1下体积分数分布Fig.8 Distributions of volume fractions of Case AS1
为了探究注入减阻剂溶液对水下回转体通气空化的影响,将注入减阻剂溶液和未注入减阻剂溶液通气空化的结果进行比较,如图9所示,其中每幅图上下2部分分别为注入减阻剂溶液和未注入减阻剂溶液工况。从整体上看,对于局部空化工况(图9(a)、(b)和(c)),注入的减阻剂溶液大大改善了水下回转体周围的空泡形态,空泡的直径更大;对于超空化工况(图9(d))通溶液对空泡的影响极小。同时,通过比较图9(a)和(c)以及图9(a)和(b)还可以发现,随减阻剂溶液注入量和通气量的增加,空泡变得更为光滑且直径更大。
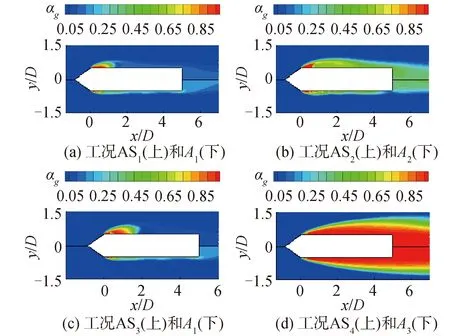
图9 减阻剂溶液注入下对通气空化不同工况的气相体积分数分布影响Fig.9 Effect of the injection of drag-reducing solution on the distributions of gas phase volume fraction in ventilated cavitation with the injection of drag-reducing solution under different cases
同样,针对水下回转体在减阻剂溶液注入和通气下的空化阻力特性进行了分析,图10给出了水下回转体在σ为0.315 0、Qa为9.42×10-4m3/s工况下注入减阻剂溶液和未注入减阻剂溶液的结果对比。从图中可以发现,在局部空化下注入减阻剂溶液后Cv大大降低,从而导致总阻力系数减小,在Qs为2.72×10-4m3/s时总阻力减小了14.08%,这是由于表面活性剂作为湍流减阻剂具有湍流减阻效应。但同时也发现在增大减阻剂溶液注入量后,虽然Cv继续减小,但此时较大的溶液注入量使得Cp增大,从而导致Cd增大。对于工况AS2(其结果并未在图10中给出),其各阻力系数Cv为0.003 6、Cp为0.292 0和Cd为0.295 6,总阻力减小了31.29%,这说明注入表面活性剂溶液的确可以减小空泡气液交界面处的表面张力,从而促进空泡的增大并减小航行阻力,在使用减阻剂溶液注入改善空化流动中需要同时使用通气方法以实现更佳的减阻效果,从而提高水下回转体的航行速度。
3.5 表面张力的影响
表面活性剂最显著的特性是降低液体的表/界面张力,为了探究表面张力的考虑对计算结果的影响,在本小节的数值模拟中以动量方程体积力源项的形式考虑了表面张力的作用。根据实验测量结果[16],选取了减阻剂表面张力为0.03 N/m。通过上文结果可知,减阻剂溶液注入和通气对水下回转体超空化流动特性的影响不大,因此这里仅分析了局部空化工况AS1和AS3。图11给出了考虑和未考虑表面张力下的气相和溶液相体积分数分布。从图中可以发现,对于工况AS1,在考虑表面张力后,水下回转体周围空泡的尺寸(直径)变化不大,而对于工况AS3,由于减阻剂溶液的注入量较大,水下回转体周围空泡的直径略有增大。
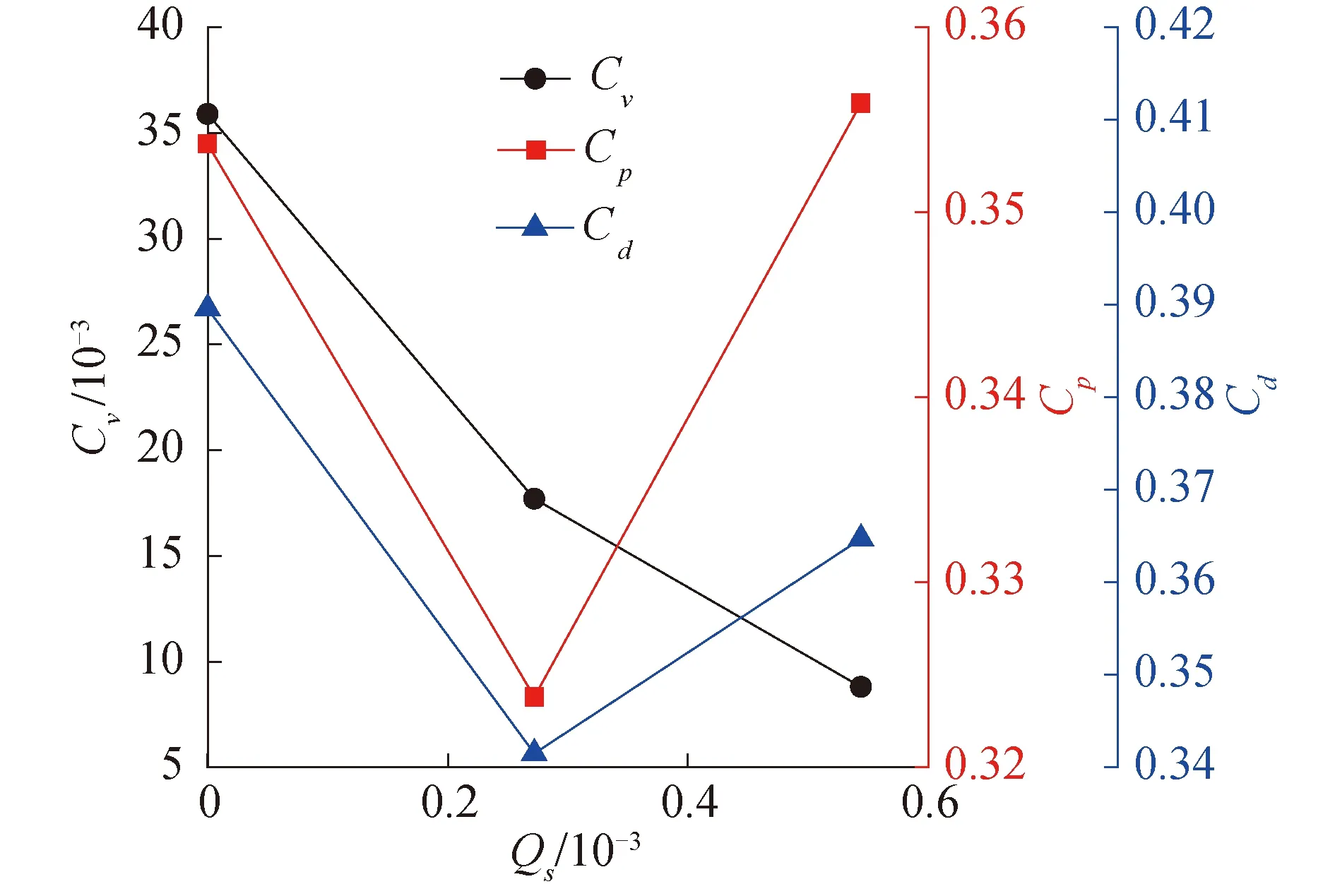
图10 不同减阻剂溶液注入量下回转体阻力系数Fig.10 Drag coefficients of axisymmetric body at different flow rates of injection of drag-reducing solution
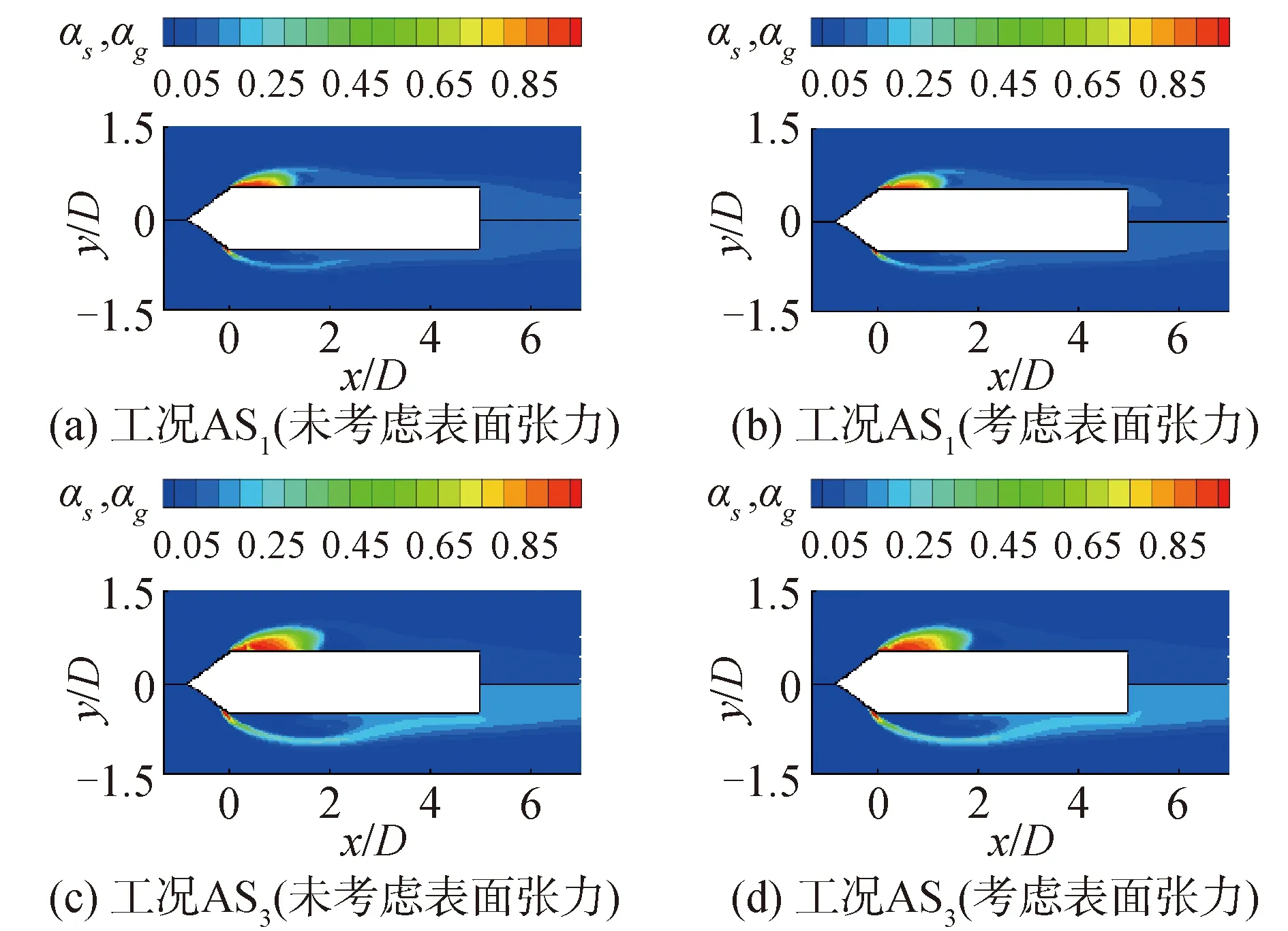
图11 未考虑和考虑表面张力下局部空化工况的气相和溶液相体积分数分布的影响Fig.11 Effect of surface tension on the distributions of the volume fractions of gas phase and solution phase without and with the consideration of surface tension under the cases of partial cavitation
表5为未考虑和考虑表面张力下工况AS1和AS3的阻力系数。从表中可以得到,在较小的减阻剂溶液注入量下,表面张力的考虑对各个阻力系数的影响极小;而在较大减阻剂溶液注入量下,表面张力的考虑使得Cv有所减小,从而使得Cd减小,这与图11(b)中观察的现象一致。图11中空泡增大的效果以及表5中阻力减小的效果不是十分明显,这可能是由于数值模拟中表面张力还不足够小,这将在以后的工作中进一步地研究。
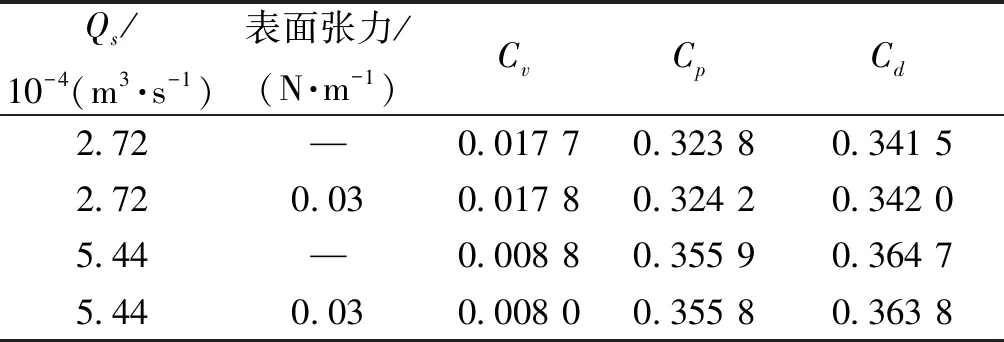
表5 表面张力的考虑对减阻剂溶液注入下通气空化回转体阻力系数的影响
4 结论
1)通气对水下回转体局部空化影响明显,即增大了水下回转体周围空泡的形态,促进其向超空化状态转变,但对超空化状态影响不大。
2)在相同通气量下减阻剂溶液的注入可以进一步促进局部空化的发展,使得水下回转体周围空泡的尺寸进一步增大,但对于超空化工况影响仍然极小。
3)随着表面张力的减小,在较大减阻剂溶液注入量下水下回转体周围空泡的尺寸略有增大。本文针对表面活性剂溶液注入影响空化流动特性的初步研究可为水下航行体的减阻增速提供新思路。
